分数がふくまれる方程式の解き方がわからん!!
こんにちは!1日に映画を5本みたKenだよー!
中1数学で勉強する方程式はまだ可愛い方だよ。だって、文字が1つしか登場しないからね。このタイプのものは一次方程式だとか、xの方程式とかと呼ばれている。
この解き方は前回の「【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜」で勉強したからもう大丈夫だよね??

じつは方程式でつまずく人が多いと言われているのは、
分数が含まれた方程式の解き方
を理解することなんだ。分数が含まれるとちょっと厄介。いままで楽勝に見えていた方程式がむずかしくみえちゃう。これは勉強する側としてはとても嫌。。
だから、今日は中1数学の方程式の解き方でつまずかないためにも、
分数がふくまれる1次方程式の解き方
を2つのステップで振り返ってみよう。
分数をふくむ方程式の解き方の2つのステップ
前回勉強したチョー基礎的な方程式の解き方を応用できるまでに、
分数の方程式ではやることが2つあるんだ。
たった2つだけ。
これさえやっちゃえばいつも通り方程式を解くだけでいいんだ。カンタンそうでしょ??
分数の方程式の解き方を説明するために、今日は、
(2x + 5)/3 = (x-4)/4
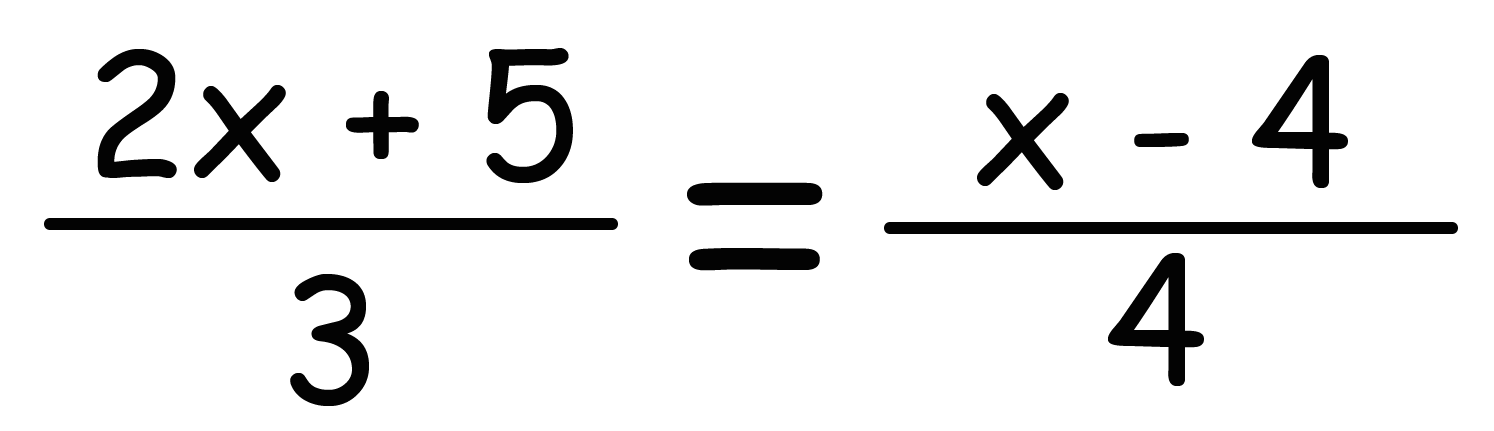
という分数入りの方程式の解き方をみていくよ!
解き方1. 分母を払う!
まず最初に「分母を払う」というワザをつかって分数の方程式をシンプルにしちゃおう。
「分母を払う」とは、
分母をなくしちゃうこと。つまり、分数を方程式から消し去ろう!ということなんだ。
そのためには具体的に、
左と右の分数の分母の「公倍数」をかけてあげればいいんだ。
えっ。公倍数がよくわからない?? Wikipediaによると公倍数とは、
2つ以上の正の整数の、それらに共通する倍数のことをいう。
とあるよ。つまり、2つ以上の数字をそれぞれ何倍かずつしてやれば同じ数になる。このとき、その「同じ数になる数字のこと」を公倍数っていうんだ。
たとえば、「3」と「4」の公倍数は12。だって、「3」を4倍したら「12」になるし、「4」を3倍しても「12」になるからね。
だからさっきの例題の、
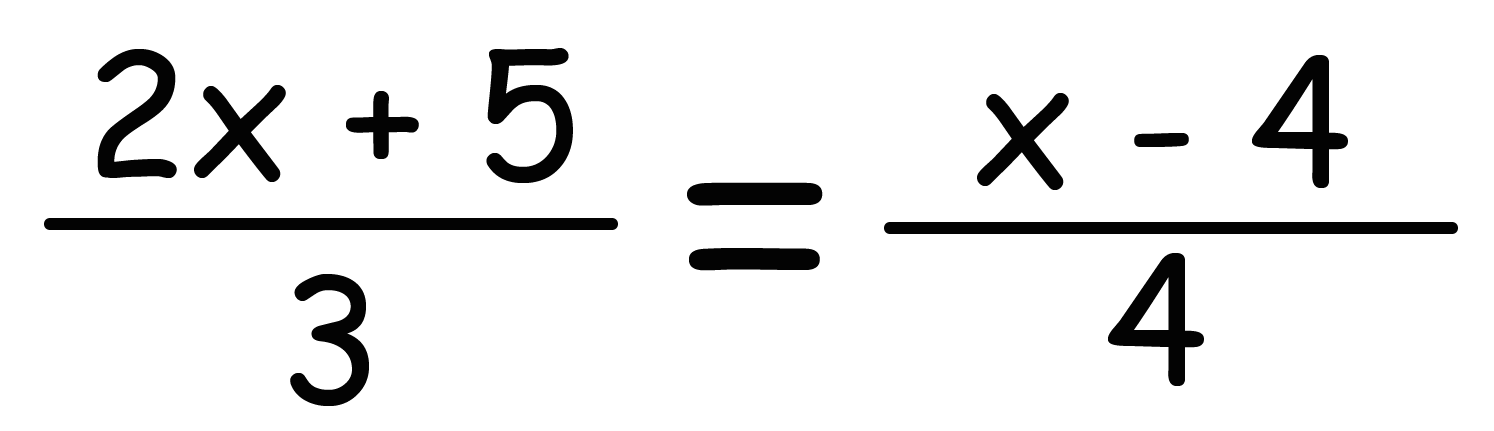
には、まず分母の「3」と「4」の公倍数12を方程式の両辺にかけてあげるんだ。等式を成り立たせるために、かならず両方に同じ数をかけてね!
そうすると、
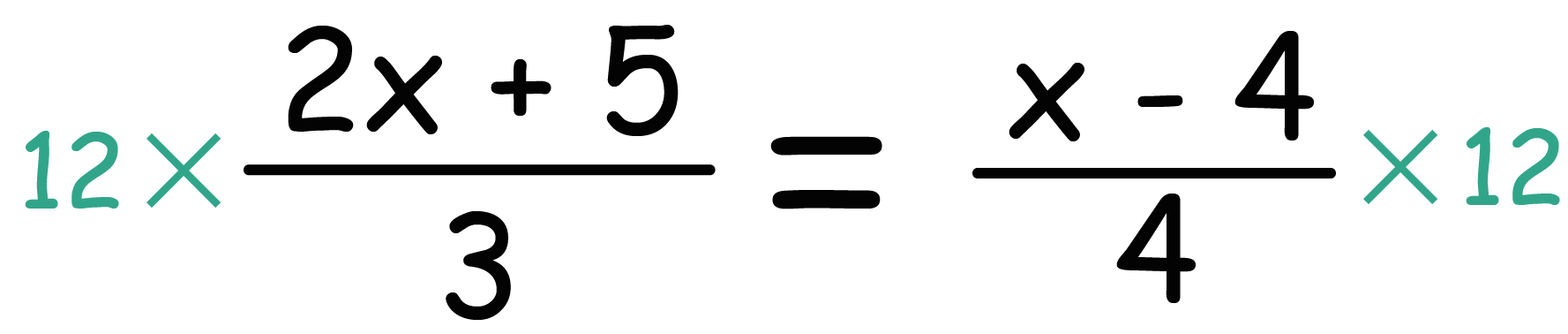
こうなるよね??
そんで、左の分母3と、右の分母4が12によって消されちゃうので、
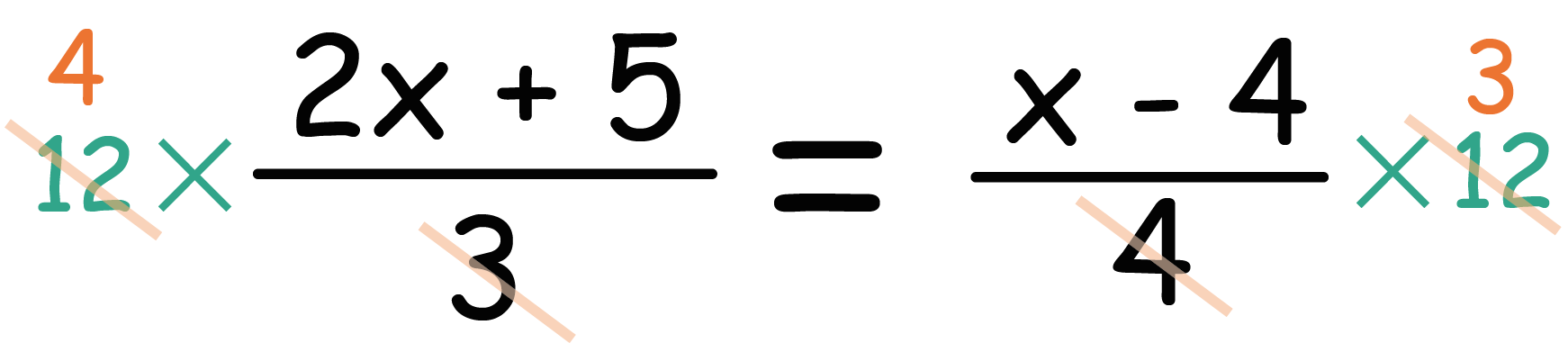
こうなる。
ここで注意してほしいのは分子をきっちり()でくくってやること。分母を払うためにかけた数字の残骸(ここでは赤い数字の4と3)で分子を()でくくるのさ。
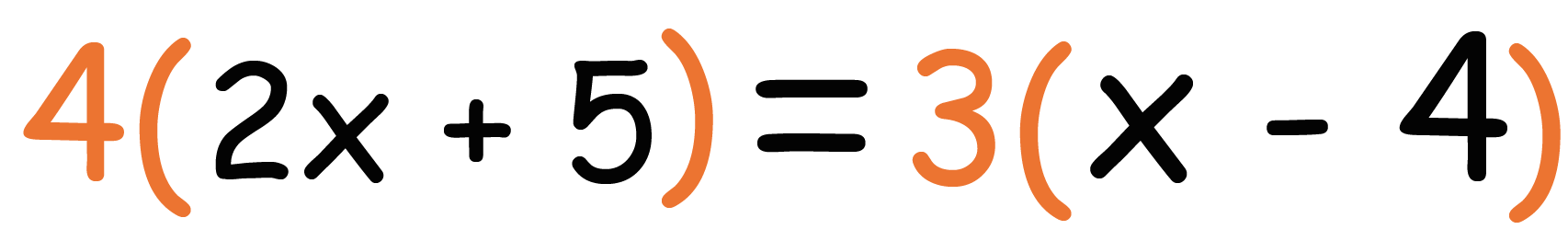
これを忘れると計算結果が異なってくるので注意してね^^
あ、分母の公倍数がよくわからん!
というときは分母の数をそれぞれゆっくりかけてみてもいいよ。たとえば、この例でいえばとりあえず「3」を両辺にかける。そんで、次に残った分母の「4」をかける。
これでもおk!
解き方2. ()を分配法則でゆっくりはずす
さて、次が一番間違いの多いところだよ。分母を払って安心しちゃう奴が多いんだ。
分母を払ったときに残った残骸で分子を包んだね???
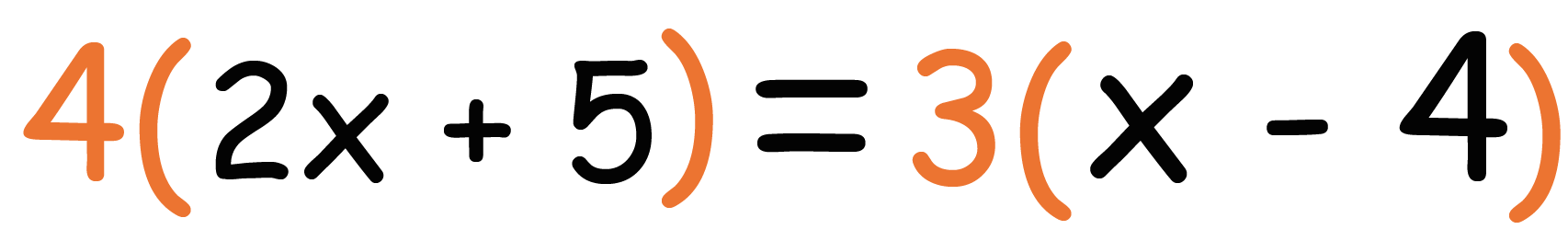
そしたら、その()を分配法則をつかってはずしてみよう。

()の外の数字を中の数字すべてにかけるのを忘れずにね!
分配法則をつかって()をはずしてやると、

8x + 20 = 3x -12
になるよね??
この方程式のカタチはチョー基本形。だから「【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜」で紹介した解き方を使ってやればすぐ解けるんだ。
xと数字の項を移行して分離させ、そしてxを裸にしてやると、
x = -32/5
分数をつかった方程式でやっかいになる解き方は上の2つだけでいいんだ。あとは基本的な方程式の解き方と同じ。ゆっくりやればとけそうだね^_^
分数の方程式の解き方もゲットだぜ??
ここまで勉強してきた分数の方程式の解き方はどうだったかな?? 分数の方程式とかむずかしそうに聞こえるけど、ちょっと手順を付け加えてやればちょちょいのちょいさ。
計算ミスをしないようにゆっくり解いてみよう!!
そんじゃねー!!
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。

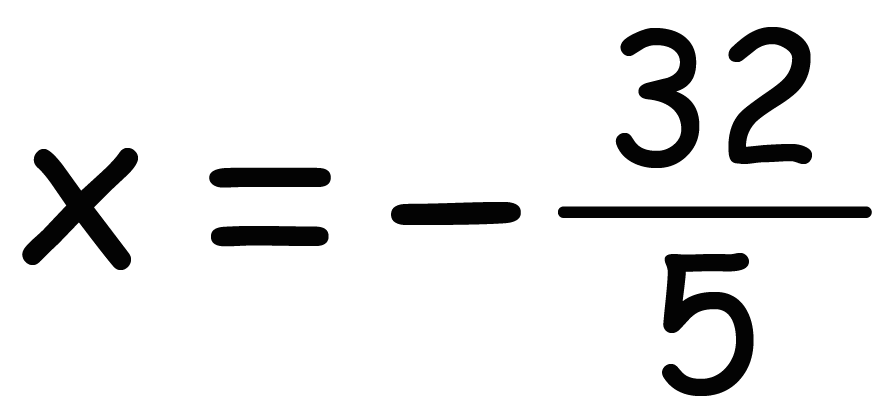



























5分の3x+2=3分の2x-1はx=1になりますか?
ならないね!最後の移項をもう一度やってみて!
ありがとうございます!
X=3でaの値を求める式で、
2− 2分のX−a=3a+x
の解き方が分かりません!
詳しく解説して頂けませんか?
2− 2分のX−a=3a+x
のxに「3」を代入してaだけの方程式をつくってみよう!
あとはaについて解くだけだ
整数と分数が混じった計算が分かりません。どうやるのですか?
整数と分数が混じってたら、分数を含む方程式の解き方でオッケー。
分母の最小公倍数を左と右にかけて、分数に消し去ろう!
3-(-2+x)/3=3x+2+5といった方程式が解けなくて…分数が1つしかない場合はどのように解くのでしょうか?
分数が1つでもある方程式は、分母を払っちゃうことが一番。
分母の数を左辺と右辺にかけて分数を消し去ろう
2分のⅹ-6 - 5分の5-ⅹ=3
の解き方がわかりません。
この場合分母をはらうにはどうすればいいのでしょうか?
分母の2と5の最小公倍数を両辺にかければいいね!
最小公倍数がわからないときは、2つの分母をかけた数(2×5)を左と右にかけるって考えるとわかりやすいね
5分の3x-3分の8=3xはx=10になりますか?
ならないね!
4/3X-5=2/X-5って
Xは-1になりますか?
ならないね!
3/x=-10の解き方がわかりません?!忙しいところ申し訳ございません….
分数=整数の計算がよくわかりません!…(>_<)教えていただけますでしょうか?!
>3/x=-10の解き方
分母を両辺にかけてみよう。
この問題だと3をかければいいのね
3x2乗-5分の6x=0
はどうやって解いたらいいですか?
>3x2乗-5分の6x=0
共通因数でくくる解き方でいけそうだね。
ヒント:共通因数は3xだ
質問じゃなくてすみません!
ただお礼を言いたかったんです!
分数とか使うのが苦手だったけど
これを見たことによって完璧に理解できました!本当にありがとうございます!
ありがとう!!励みになるぜ!!
2―5x+1/6 =1/2
の解き方はどうすればいいでしょうか?
分母が別々の時はどうしたら?
>2―5x+1/6 =1/2
分母を払ってみよう。
分母が2と6だから、最小公倍数の6をかければいいね。
最小公倍数がわからないときは、分母をかけた値(この場合だと2×6)を両辺にかければいいの
>分母が別々の時はどうしたら?
分母の最小公倍数を両辺にかけてみよう!
-3/4+2x=-7/12-3x
これはどのように解けばいいでしょうか?
>-3/4+2x=-7/12-3x
分母払ってみようぜ。
分母は4と12かな?
こいつらの最小公倍数の12を両辺にかければいいよ
-x+6=½x+3 はどのように解きますか?
>-x+6=½x+3
両辺に分母の2をかけて
分数を消し去ろうぜ
3/2x=8の解き方を教えてください。
>3/2x=8
分数の分母の数を両辺にかけてみよう!
Thank you よくわかったぜ。分数と整数が、混じってても楽勝だな。これで。
3(x-9)=4(7-x)が何回やっても
3X-27=28-4X
3X-4X=28+27
になるんですがどうしたらいいんでしょうか?
X/60+X/40=5
お願いしまーす。
3 / ( 3 + 18.8 + a ) = 0.12
この解き方がわかりません。
>3(x-9)=4(7-x)が何回やっても
3X-27=28-4X
3X-4X=28+27
になるんですがどうしたらいいんでしょうか?
移項の時の符号が間違えてるよ!
-4xを左辺に移項したら+4xになるはず
>X/60+X/40=5
分母の60と40の最小公倍数120を両辺にかけてみよう
>3 / ( 3 + 18.8 + a ) = 0.12
分数と小数が混じっているときは、小数を分数に直して
分数だけの方程式にしてみよう。
あとはいつも通り分母を払えばいいね
5分の4X=8
などの分数X=整数
の解き方が分かりません。
教えてください。
>5分の4X=8
分数の項が一つでも含まれている場合は、
分母を払ってしまおう。
この場合、分母の5を両辺にかければいいね
少し問題が違ってしまうのですが、
-3x×-6=1/2x+5×4 の解き方を
教えてください
4/3x-5=2/x-5
(3x×4/3x)-(3x×5)=(3x×2/x)-(3x×5)
4-15x=6-15x
-15x+15x=6-4
0x=2
0xになってしまいますが、0xはx=2でいいんでしょうか?
>-3x×-6=1/2x+5×4
まずは掛け算を済ませてしまおう。
そのあと、分数を消すために分母の2を両辺にかけてみて
>4/3x-5=2/x-5
(3x×4/3x)-(3x×5)=(3x×2/x)-(3x×5)
4-15x=6-15x
-15x+15x=6-4
0x=2
この場合、2にはならないね!
0にもならないから多分問題が間違えてるんじゃないかな!
4分の1+x=-2分の1
のxに当てはまる数字と途中式を教えてください
>4分の1+x=-2分の1
分母の最小公倍数を両辺にかけてみよう。
この場合、4だ!
6分のX+4分のX=5 というのはどうすれば用のでしょうか?
教えてください
20/(100+x)*100=20がわかりません。
Xが分母にはいっている時は、どうしたらいいのでしょうか。
>6分のX+4分のX=5
分数を払ってみよう。
分母の最小公倍数を両辺にかければいいんだよ。
この場合でいうと12かな
>20/(100+x)*100=20
xが分母に入ってるのが嫌だったら、
分母と同じやつを両辺にかけてやろうぜ。
X/3-1=X/4+1
12(X/3-1)=12(X/4+1)
4X-12=3X+12
X=24
だと思いましたが…
答えはX=7と言われました。
なぜですか?
すみませんでした。
X-1/3=X+1/4で
X=7でした。お騒がせしました。
>X/3-1=X/4+1
12(X/3-1)=12(X/4+1)
4X-12=3X+12
X=24
あってるね!
整数=分数混じりのx
の場合ってどうしますか?
>整数=分数混じりのx
分母を払って、分数をなくす!
8x+20=3xー12がx=ー32/5になるんですか?
>8x+20=3xー12がx=ー32/5
なるよ!
移項してxの前の係数で両辺を割ってる!
分数−4分のx−9✕3の場合、分母4の隣にある−は、どういう意味なんですか?
>分数−4分のx−9✕3の場合、分母4の隣にある−は、どういう意味なんですか?
分母にマイナス1がかけられていると思えばいいよ。
分母にマイナスを無くしたかったら、分母と分子にマイナス1をかけてやればいいかな
760×X/100=38 の答えが、5になりません。
どうしたらいいですか?
4分の3x=2x+2分の1の解き方が分かりません
教えてください
>760×X/100=38
両辺に100をかけて分数を消す。
あとはxの前についている係数760で両辺を割るといいよ
>4分の3x=2x+2分の1
分母払って分数を消し去ろうぜ。
分母の最小公倍数4を両辺にかけてみよう
3+4X=-9 の解き方教えてください
>3+4X=-9
3を右辺に移項して、
xの係数で両辺を割ってみよう
3分の2x+5=9分の2x-3分のx+2
はどうしたら良いですか?
>3分の2x+5=9分の2x-3分のx+2
分母の最小公倍数9をかけて分母を払ってみよう
4分のa+5-3分のa+2=1の解はa=-5なんですが何回解いても-6になります。何故なんでしょうか?
4分のa+5-3分のa+2=1の解はa=-5なんですが何回解いてもa=-6になります。何故なんでしょうか?
>4分のa+5-3分のa+2=1
-5になるね!
分母の最小公倍数12を両辺にかけてやれば計算できるはず。
注意点としては、
1. 両辺に12をかけること
2. -3分のa+2の分母を払うときの符号計算かな
もう一回トライしてみよう!
分母払う時に気をつけて!
240/x + 60/x + 10 = 50
の、答えって何ですか?
解き方を教えてください!!
>240/x + 60/x + 10 = 50
分母の最小公倍数をかけてみよう。
240と60が分母だから、240を両辺にかければいいのね。
x-3分の2x+1=5
>x-3分の2x+1=5
分母の3を両辺にかけて分数を消し去ろう
9✕3分の8a+1
の解き方を教えてください……
>9✕3分の8a+1
これは通分だね。
最後の整数1の分母を9×3にしてみよう
20 = 40 ÷(40 + x ) × 100
を教えてください
>20 = 40 ÷(40 + x ) × 100
分母の(40+x)を両辺にかけると解きやすくなるよ!
3(x-2)-4(4-x)分の6=6
の解き方が分かりません
>3(x-2)-4(4-x)分の6
分母を両辺にかけてみよう!
4分の3X➖6分の1=6分の5X➖3分の2の計算の仕方がわかりません。教えてください。
>4分の3X➖6分の1=6分の5X➖3分の2
分母の最小公倍数を両辺にかけてみよう!
4、6、3の最小公倍数は何かな?
a分の1+b分の1=c分の1のaの解き方が分かりません。教えてください。
>a分の1+b分の1=c分の1のaの解き方
分数を含む等式の変形だね。
bを右に移項して、通分して、両辺を逆数にしよう
x+100分の5x=441のやり方が分かりません
教えてください!お願いします!
>x+100分の5x=441
分母の100を両辺にかけてみよう!
3分の4X-5=2X-9
の解き方を教えてください!!
お願いします!
>3分の4X-5=2X-9
分母の3を両辺にかけて分数を消し去ろう!
15/x+60/15=8/xー60/20の解き方を教えてください。
>15/x+60/15=8/xー60/20の解き方を教えてください。
分母の最小公倍数(この場合でいうと60かな)を両辺にかけて
分数を消し去ろう
>15/x+60/15=8/xー60/20の解き方を教えてください。これの質問のつづきなのですが
8/xはどうすればよいにでしょうか?これは道のりの問題でx=道のりの式なのですがこれはx=10
になりますか?間違い直しがあるのでお願いします。
質問です。
3分の4Xの二乗➕2Xはどうなりますか?
X一3分の2Xー1=ー1
の時はどーしたらいいんですか??
>3分の4Xの二乗➕2X
これは文字式?
>X一3分の2Xー1=ー1
両辺に分母の3をかけて分数を消し去ろう
例文で出した2x+5/3=x−4/4で8x+20=3x−12まではできたけどその後の
x=−32/5がどうやってやったかよくわかりません
3分の2X+4=-4分の3X-2-2
は最後の-2が分子に入っていないんですけど
それも3をかけていいんですか?
後、この答えはどうなりますか?
>例文で出した2x+5/3=x−4/4で8x+20=3x−12まではできたけどその後の
x=−32/5がどうやってやったかよくわかりません
一次方程式の解き方を使っていくよ。
xの項を左に、それ以外を右に移項して同類項をまとめて、
最後にxの前の係数で両辺を割ればいいのよ
xの値が-3 -2 -1 0 1 2 3
yの値が3/2 1 1/2 0 -1/2 -1 -2/3
という表がありyがxに比例する関係を表していると説明したかったので、分数の分母が2となっているから分子に2を掛けたらいいと説明しても、なぜ分子にかけるだけで整数にはかけないのか?と言われ、どう説明したものかと…悩んでおります。
分かりやすい解答方法があれば教えてください!
>3分の2X+4=-4分の3X-2-2
は最後の-2が分子に入っていないんですけど
それも3をかけていいんですか?
この場合、分母(3と4)の最小公倍数12を両辺にかけるよ。
分子に入ってないやつにもかけてね
>xの値が-3 -2 -1 0 1 2 3
yの値が3/2 1 1/2 0 -1/2 -1 -2/3
という表がありyがxに比例する関係を表していると説明したかった
比例ということは、次の2つのことがわかればオッケーです。
1. 原点を通ること(xが0のとき、yが0になってるよね)
2. xが2倍になると、yも2倍になってること(xが1から2に変化したとき、yは-1/2から-1になった)
最後はちょっとややこしいけど、-1/2 を2倍すると-1になることを説明しましょう! 分母の2がうまい感じに約分されて消え失せるはずです
x-4/3-5x+2/4=0 教えてください
>x-4/3-5x+2/4=0
分母の最小公倍数をかけて分数を消し去ろう!
360/120=12/xがわかりません!
計算過程も一緒にお願いします!
>360/120=12/x
両辺に360をかけてみようぜ!もしくは360/120を先に約分してもいいね
x-3= 3/1(5x-1)のやり方がわかりません
よかったら、やり方教えてくれませんか?
X=2分の1(2分の1X+10)はどうすれば良いでしょうか?教えてください。
(X-4):4=(3X-6):16
この比例式の解き方を教えてください!!
>x-3= 3/1(5x-1)
分母の3を両辺にかけて分数を消し去ろう
>X=2分の1(2分の1X+10)はどうすれば良いでしょうか?教えてください。
両辺に2をかけて()の外の分数をいったん消し去ろう
あとはもう一回2をかけて分数を根絶しよう
>(X-4):4=(3X-6):16
内向の積 外向の積を使って比例式を展開してみよう!
ありがとうございました(≧∇≦)これでやり方が良くわかるようになりました!
おお!よかった!^^
-6=4分のxのようなxが分子になっている場合はどう計算すればいいんですか?
>-6=4分のxのようなxが分子になっている場合はどう計算すればいいんですか?
分母の4を両辺にかけて分数を消し去ろう
例えば
3X-2分の3=4分の7-5
これって全部の項に公倍数の4をかけて
12X-6=7-5
っていう風になるんですかね…?
>例えば
3X-2分の3=4分の7-5
これって全部の項に公倍数の4をかけて
12X-6=7-5
っていう風になるんですかね…?
おしい!一番右の-5にも4をかけてね
5/4X-1=2/X+1の回答がX=4になるらしいのですが、どうしてその答えになるのかどうしてもわかりません!解説をよろしくお願いします泣
>5/4X-1=2/X+1の回答がX=4になるらしいのですが、どうしてその答えになるのかどうしてもわかりません!解説をよろしくお願いします泣
分母の最小公倍数(分母は5と2だよね?)の10を両辺にかけてみよう!
分数を消し去るのが先決だ
0.002=(x-200)-(500/2.62)/500-(x-200)
>0.002=(x-200)-(500/2.62)/500-(x-200)
まず両辺を1000倍して左辺の小数を消し去ってみよう
2分のx-3-4分のx-1=1の方程式を解きなさい。という問題の解き方を教えて下さい‼
>2分のx-3-4分のx-1=1の方程式を解きなさい。という問題の解き方を教えて下さい‼
分母の2と4の最小公倍数4を両辺にかけて分数を消し去ろう
4分のa−(2a−8)の仕方が分かりません。
教えて下さい!
>4分のa−(2a−8)の仕方が分かりません。
教えて下さい!
通分してみよう!分母を4に揃えればいいのさ
4分のa−(2aー8)の仕方が分かりません。
教えて下さい!
>4分のa−(2aー8)の仕方が分かりません。
通分してみようぜ!
8分のx − 6分のx−7 =1はどうなりますか?
教えてください!
>8分のx − 6分のx−7 =1はどうなりますか?
分母の8と6の最小公倍数を両辺にかけてみようぜ
20+X×100分の9=(500+X)×100分の5
解き方を教えてください!
ちなみに答えはX=125です
>20+X×100分の9=(500+X)×100分の5
分母の100を両辺にかけて分数を消し去ろう
6(2分のxー1➕3分の2xー3)ってなんですか?
>6(2分のxー1➕3分の2xー3)
分配法則で展開してみよう!
お世話になりました!わかりやすかったです!
(− 6)×a − 4分の2の解き方がわかりません何回やっても不正解なんですどうしたらいいですか(°▽°)
24=100+X/5+X✖️100
食塩水と濃度を計算する方法と問題レベル2
の例題なのですが、この次の
24(100+X)=100(5+X)
になるまでの仕方がわかりません。100+Xはなぜマイナスがつかないのかも教えてください。
おお!よかった〜
>(− 6)×a − 4分の2
これは通分だね。先頭の-6aの分母を4に合わせてやろうぜ
>24=100+X/5+X✖️100
食塩水と濃度を計算する方法と問題レベル2
の例題なのですが、この次の
24(100+X)=100(5+X)
になるまでの仕方がわかりません。100+Xはなぜマイナスがつかないのかも教えてください。
両辺に100+xをかけてるんじゃないかな〜
中学2年です。分数+分数の式と、分数=分数の式の解き方の違いがわかりません!
両方、x,yの混じった式が分子で、=の方は連立方程式の一部です。
+の方は、分母を揃えて、1つの分数にした形が答え方と教えて貰ったのですが、何故、分母の最小公倍数をかけて分子の式のみの形にしてはいけないのですか?
また、=の時は分母の最小公倍数をかけて、分子の式のみにして式を解いてもいいのですか?違いが分かりません。
>中学2年です。分数+分数の式と、分数=分数の式の解き方の違いがわかりません!
両方、x,yの混じった式が分子で、=の方は連立方程式の一部です。
+の方は、分母を揃えて、1つの分数にした形が答え方と教えて貰ったのですが、何故、分母の最小公倍数をかけて分子の式のみの形にしてはいけないのですか?
また、=の時は分母の最小公倍数をかけて、分子の式のみにして式を解いてもいいのですか?違いが分かりません。
なぜ、
分数=分数の式
は分母の最小公倍数をかけて、分子の式のみにして式を解いてもいいのか?
を考えるといいね。じつは、それは等式の性質によるもので、
等式が成り立っているなら、両辺に同じ数をかけてもいい
というルールがあるからなんだ。
分数+分数の式は等式じゃないから分母の最小公倍数をかけて、分子の式のみにできないんだ
十分の九x=(x-20)×(1+二分の一)の解き方を教えてください。
両辺に10をかけて分数を消し去ろう!
ヒロアカ好きですか?
あなたの言葉を聞いて人生変わりました。あなたのおかげで88点取れました。数学で、あざっす。
ヒロアカ知らんかった笑
多分、当たり前のことすぎておかしいと思いますが、『−4分のX』で、×4をしますよね。その4は−4ですか?
乗法の時はかけられる数とかける数っていうのは記号を同じにしなきゃならないのですか?疑問ですw
分数がなくなればいいから符号はどっちでもいいかな!
とにかく色々教えてください笑笑
比例のやつもなかなか頭に入ってきません!どうにかしたいです!笑笑
あなたのおかげで89点取れました笑笑ありがとうございます!これからもあなたの投稿見て頑張ります!これからもお願いします!
3分のX-3=4分のX+7
が解けません。どうすれば解けますか?
分母の3、4の最小公倍数12を両辺にかけてみよう!
sinθ=A分のCの公式で、 直角三角形 斜辺A垂辺Cとし、斜辺A=sinθ分のCとなるまでのやり方がわからない? 両方にC分の1を掛けるとA=C分のsinθになってさまうわからない?教えてください。
x+36/x=5/3 の方程式の解き方を教えてください。
x-58/x=32/8これ解りません!
塾の宿題が難しいです
分数の計算にさらに数字が着くとどうなりますか?そやら、らやらやらやはやらやらやらたら
ありがとうございます!わかりやすい説明で参考になりました!
分数x=分数xの計算ってどうすればいいかわからないです。教えて下さい
解けて当然!!
x=-2分の1のとき
3分の2x+4
ってどうやってするんですか
根っからの文系なので答えがX=―32/5になる方法が分かりませんでした。
このやり方が正解かどうかわからないのですが
8x+20=3x-12
8x-3x=-20-12
5x=-32
X=-32/5
でよろしいのでしょうか?
3分の2b+bの解き方を教えてください!
よろしくお願いします
4/3x=20は、どうやって解くんですか?
答えは15らしいのですが、いくらやっても15になりません。
計算方法を教えて頂きたいです。
X>-2とX≧-3分の7の共通因数がX>2になるのはなぜですか?
x3x83かける=3x-18x675029ー2×3の解き方を教えてくれる?
6分の5x+2分の1=3分の2x
みたいな式ってどうやって解くんですか?
5x=30ってどう解けばいいんですか
2分のx+3−3分の2x +1=1という方程式の解き方を教えてください。
これを参考にして中学校の問題をまたスラスラ解くことが出来ました。これからも参考にしていきたいと思います!
4分の3x=1-3分の8-x 何になるんですか?
3×Xって3Xですか?
左辺の数は分数で通分したけど、右辺の数が
整数だったとき、それも「一分のその数」にして
通分した方がいいのか
6分のエックス+2 = 2分のエックス− 3どうやってどういうんですかどうやって解くんですか
6x分数の直し方を教えて下さい!
分母払おうぜ!分母の最小公倍数6を両辺にかけよう
kenさんの解説、凄くわかりやすかったです!
有難う御座いました!苦手が無くなりそうです。
役に立ったよ〜!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
6分の5x=―40って、答えは何になるんですか?
5+ひゃくぶんのさんx=ひゃくぶんのななxの答えを教えて下さい
分数にも答えにもxが入っているしきはどうしたら解けますか?
とっっっっってもわかりやすかったです。ありがとう!!
kenさんのお陰で分からなかった方程式の分数が分かるようになりました感謝します。^_^
8分の1x=マイナス4分の3の、答えはどうなりなすか
5分の1x =2 教えてください
5分の2x =8教えてください
12;7分の3=x+1を教えて下さい