三角形の相似条件は3つもあるの??
こんにちは!この記事をかいているKenだよ。犬なでたいね。
中3数学では、
相似
を勉強していくよ。
この単元を攻略するために知っておきたいのは、
三角形の相似条件
ってやつ。
これはどういうことかっていうと、
三角形が相似になるための条件
ってものなんだ。

つまり、相似条件を満たしていれば、
2つの三角形が拡大・縮小の関係にある
っていえるわけね。
大きくしたり小さくしたりすると重なるってわけ。

今日はこの、
三角形の相似条件をわかりやすく解説していくよ。
よかったら参考にしてみてね。
2分でわかる!三角形の3つの相似条件
三角形の相似条件にはぜんぶで、
3つあるんだ。
- 2つの角がそれぞれ等しい
- 3辺の比がすべて等しい
- 2辺の比とその間の角がそれぞれ等しい
使ってなれるのが一番だけど、
はじめは見ておぼえてみようか。
相似条件1. 「2つの角がそれぞれ等しい」
まずは一番使うことが多い、
2つの角がそれぞれ等しい
っていう三角形の相似条件。

これは簡単にいっちゃうと、
2つの角が等しい三角形同士は相似
ってことがいえるの。
たとえば、そうだな。
つぎの△ABCと△DEFを思い浮かべてみて。
もし、こいつらの2つの角が、
- 角B = 角E = 58°
- 角C = 角F = 33°
ってかんじで等しかったとしよう。

このとき、
△ABCと△DEFは相似な図形といえるんだ。
なぜなら、
2つの角がそれぞれ等しい
っていう三角形の相似条件をみてしてるからね。
- 角B と 角E
- 角C と 角F
の2つの角の組が等しいじゃん?
でもね、
もし、角Fがちょっと気まぐれで、
角F = 32°
になっちゃったとしよう。

このとき、もうこいつらは相似なんかじゃない。
なぜなら、
1組の角(角Bと角F)しか等しくないからね。
こんなかんじで、
必ず2つの角が等しいかどうかチェックしようぜ。
相似条件2. 「3組の辺の比がすべて等しい」
2つめの三角形の相似条件は、
3組の辺の比がすべて等しい
ってやつだ。
対応する辺の比をそれぞれ計算してみて、
ぜーんぶ等しかったら相似っていえるんだ。

たとえば、△ABCと△DEFの辺の長さがそれぞれ、
- AB = 5 cm
- BC = 3 cm
- AC = 7 cm
- DE = 7.5 cm
- EF = 4.5 cm
- DF = 10.5 cm
だとしようか。

このとき、この2つの三角形たちは相似な関係にあるんだ。
なぜなら、
対応する辺どうしの辺の比がそれぞれ、
- AB : DE = 5 : 7.5 = 2 : 3
- BC : EF = 3 : 4.5 = 2 : 3
- AC : FD = 7 : 10.5 = 2 : 3
になってるからね。
ぜーんぶの対応する辺の比が「2:3」でいっしょ。
だから、
3組の辺の比がそれぞれ等しい
っていう相似条件をみてしてるっていえるわけ。
これはけっこうだるい相似条件だね。
相似条件3. 「2組の辺の比とその間の角がそれぞれ等しい」
最後の相似条件は、
2組の辺の比とその間の角がそれぞれ等しい
だ。
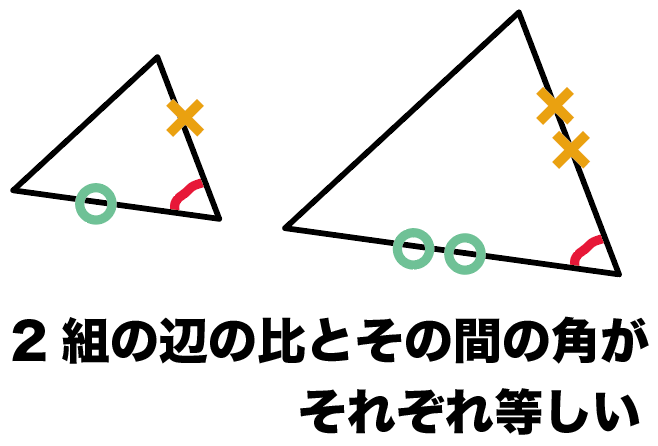
三角形の2つの辺どうしの比が等しくて、
なおかつ、
そいつらにサンドイッチされてる角まで等しい。
このとき、2つの三角形は相似であるっていえるんだ。
たとえば、△ABCと△DEFの2つの辺がそれぞれ、
- AB = 5 cm
- AC = 7 cm
- DE = 7.5 cm
- DF = 10.5 cm
だったとしよう。
んで、その2つの辺にはさまれてる角の、
- 角A
- 角D
が偶然、23°になってたとしよう。

このとき、
△ABC ∽ △DEF
がいえるんだ。 なぜなら、
2組の辺の比が、
- AB : DE = 5 : 7.5 = 2 : 3
- AC : DF = 7 : 10.5 = 2 : 3
で等しくて、
なおかつ、その間にすっぽり収まってる、角Aと角Dが、
角A = 角D = 23°
になってるからね。
2組の辺の比とその間の角がそれぞれ等しい
っていう相似条件がつかえちゃうよ。
もし、もしも、だよ?
間にはさまってる角度が途中でごねて、
角D が 30°になっちゃったとしよう。

このとき、もうすでにこいつらは相似じゃなくなっちゃう。
なぜなら、2組の辺の比しか等しくないからね。
残念!!!!
三角形の相似条件おぼえられない・・・・
えっ!?
三角形の相似条件がおぼえられないだって!??
そうだね。
そんなときは、
2組の角がそれぞれ等しい
っていう1番目の相似条件だけでもおぼえておこうw
なぜなら、
中学数学でつかう相似条件は、
だいたい80%が「2組の角がそれぞれ等しい」
だからね。
残りの相似条件の、
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角がそれぞれ等しい
があとの20%をしめるってかんじ。

だから、
まあ、余裕がなかったら、
2組の角がそれぞれ等しい
だけでもおさえてね。
時間があるなら3つの相似条件をたたきこんでおこうぜ。
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。















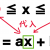










2組の辺の比と間の角が等しいの条件の時、例えば上の三角形の場合AB:AC=5:7 DE:DF=5:7 だから…
でもいいんでしょうか?
>2組の辺の比と間の角が等しいの条件の時、例えば上の三角形の場合AB:AC=5:7 DE:DF=5:7 だから…
ABとAC、DEとDFに間に挟まれる角が等しいなら大丈夫だね
最後の太字のところの、相似条件「2組の辺の比と間の角が等しい」が、「2組の辺とその間の角がそれぞれ等しい」になってますよ
ありがとう
塾の宿題でとてもややこしく辺がわからなかったり相似比がややこしかったりとしてわかりません。
難しめの相似のかいせつがあったら助かります!
応用問題が出るのを(相似)楽しみにしています。
2つの角がそれぞれ等しいというところで ‘1組の角(角Bと角F)しか等しくならない’ ではなく
‘1組の角(角Bと角E)しか等しくならない’ではないでしょうか