二次方程式の解き方を見分けるコツ??
こんにちは!この記事をかいているKenだよ。スペース最高。
二次方程式の解き方をたくさんならってきたね。
ざっと数えるだけ、6つもある。
解き方がたくさんあって便利なんだけど、
どの解き方つかえばいいかわからないんだよね。
せめて、
二次方程式の解き方を見分けるコツ
とかあれば助かる・・・・
そこで今日は、特別に、
二次方程式の解き方の見分け方
を紹介するよ。
よかったら参考にしてみてね。
二次方程式の解き方を見分ける1つのコツ
二次方程式の解き方を見分けるコツは1つ。
それは、
消去法で解き方を選ぶ
だ。
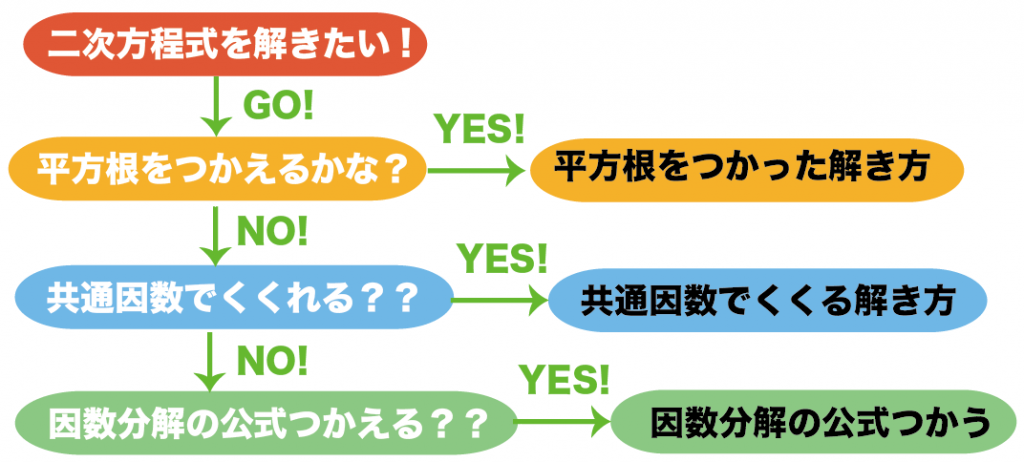
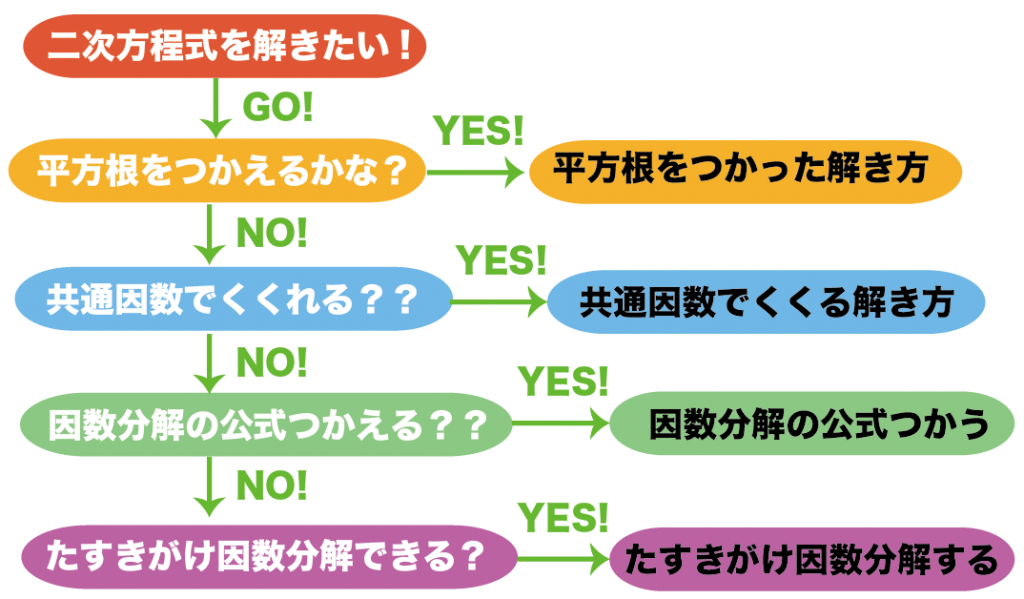
- 平方根の解き方がつかえる??
- 共通因数でくくれる??
- 因数分解の公式をつかえる??
- たすきがけの因数分解できる??
- 解の公式をつかう??
- 平方完成をつかう。
っていう6つの解き方がつかえるか、上から確認していくのさ。
全部の解き方で解けなかったら諦めよう。
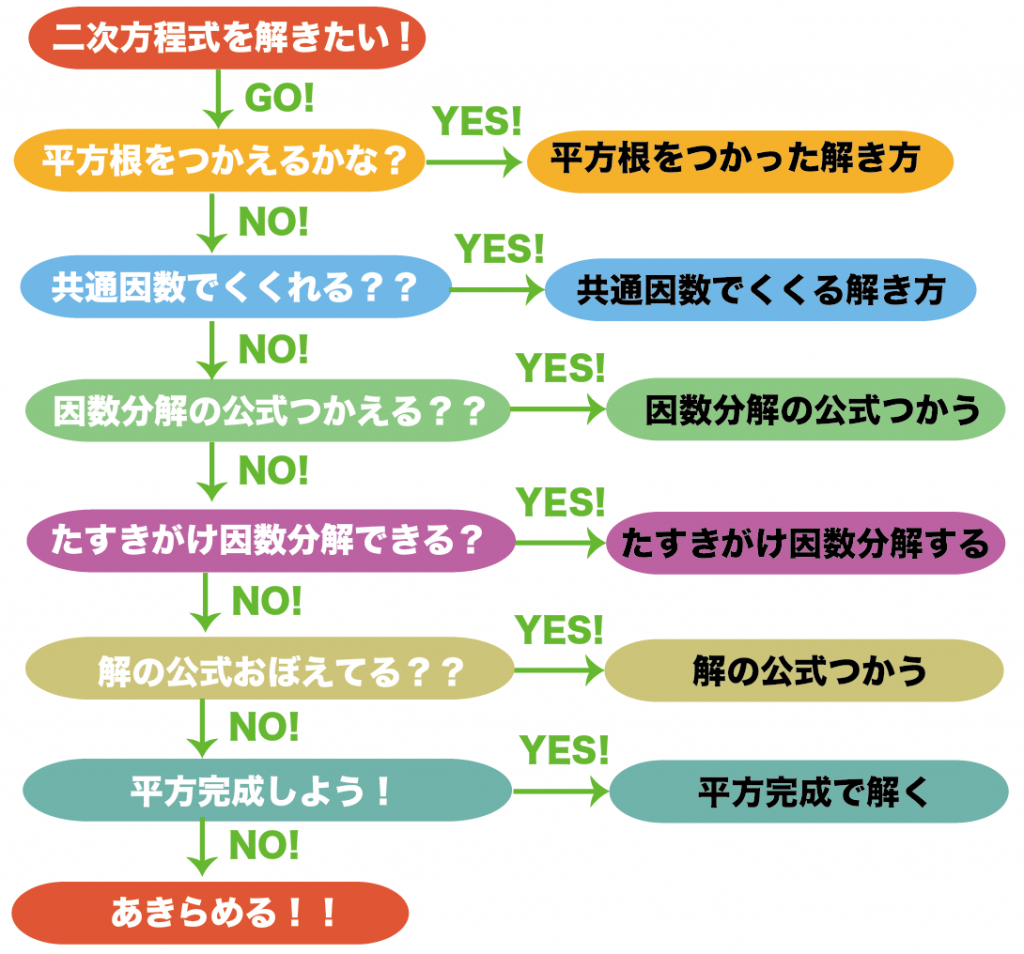
それぞれの解き方を確認してみようね。
解き方1.「 平方根でイケル??」
平方根を使えるか確認してみて。

見分け方のコツは1つ。
それは、二次方程式のかたちが
(xをふくむ式)の2乗 = A
になっているか、もしくはソレに変型できるか確認すればいいのさ。

たとえば、
(x-4)² -11 = 0
っていう二次方程式があったとしよう。

こいつはみたかんじ、
(xをふくむ式)² = A
の形にもっていけそうだ。
だって、11を右辺に移項すればいいだけだからね。
このタイプの2次方程式なら、
- 移項
- 平方根を求める
- 移項
の3ステップでとけちゃうよ。
くわしくは、平方根をつかった二次方程式の解き方を復習してみて。
実際に右辺に11を移項して解くと、
(x-4)² -11 = 0
(x-4)² = 11
x – 4 = ± √11
x = 4±√11
になるね。
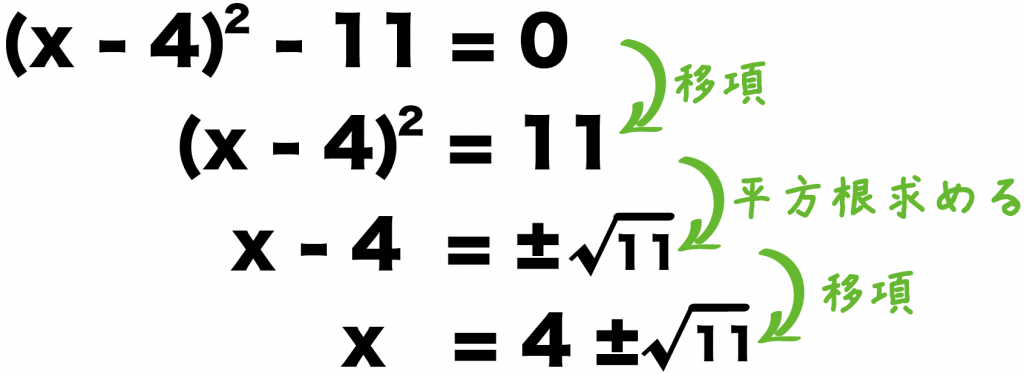
平方根をつかう解き方がいちばん簡単。
こいつで二次方程式が解けるか、まず確認してみて。
解き方2. 「共通因数でくくれる??」
共通因数でくくれるか確認しよう。
項が2つの二次方程式のとき、つかうことが多いね。
たとえば、つぎの二次方程式とか↓↓
3x² = 7x
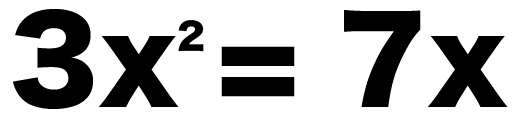
この二次方程式の解き方なら、3ステップでとけちゃう。
- 移項する
- 共通因数でくくる
- 一次方程式を解く
⇒くわしくは「因数分解の公式をつかわない二次方程式の解き方」をよんでね。
実際にといてみると、
3x² = 7x
3x² – 7x = 0
x(3x – 7) = 0
x = 0, 3分の7
になるね。
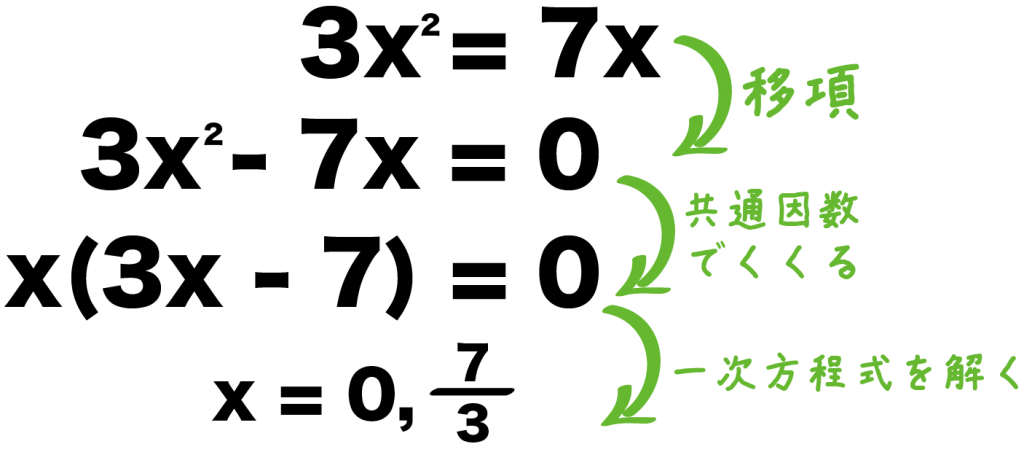
解き方3. 「因数分解の公式つかえる??」
平方根でも解けないし、共通因数でもくくれない・・・・
そんなときは、
因数分解の公式をつかった二次方程式の解き方
だ。
この解き方では、
因数分解の公式で二次式を因数分解して、一次方程式をつくっていくよ。
たとえば、つぎのような問題ね。
x² + 6x = -8

このタイプの二次方程式は3ステップでとけちゃう。
- 移項
- 因数分解の公式つかう
- 一次方程式をとく
⇒くわしくは「因数分解をつかった解き方」をよんでみて。
実際に、さっきの二次方程式の、
x² + 6x = -8
を因数分解の公式をつかってといてみると、
x² + 6x = -8
x² + 6x + 8 = 0
(x +2) (x+4) = 0
x = -2, -4
になるね。

因数分解の公式をよーく復習しとておいてね^^
解き方4. 「たすきがけ因数分解つかえる??」
因数分解の公式つかえねえええー
そんなときは、
たすきがけの因数分解がつかえるか粘ってみよう。
たとえば、つぎの二次方程式で活躍するね。
5x² – 11x + 6 = 0

因数分解の公式を使おうとしても・・・・・
ぐっっっっ
使えない!!
ってなるはず。
そういうときは「たすきがけの因数分解」をつかえばいい。
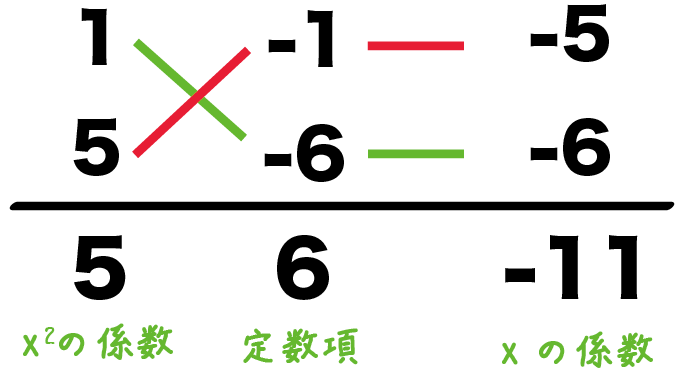
2次方程式の係数を、
- xの2乗の係数
- 定数項
- xの係数
の順番にヨコにかく。
んで、
かけたら「xの2乗の係数」、「定数項」になる数字をたすきがけで考えると、
1 -1 -5
5 -6 -6
———–
5 6 -11
になる。
よって、二次方程式は、
5x² – 11x + 6 = 0
(x-1)(5x-6) = 0
になるね。
今まで通り、一次方程式をといてやると、
x = 1, 5分の6
になるね。
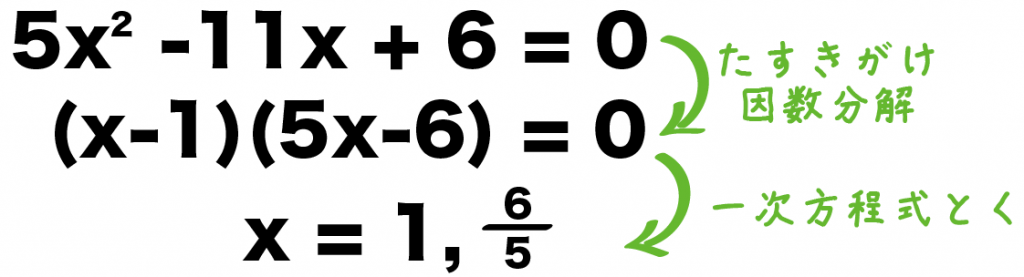
解き方5. 「解の公式をつかう」
因数分解の公式も、たすきがけも無理。
そんなときは最終兵器、
解の公式
をつかおう。

解の公式はどんな二次方程式でもとける公式だったね??
覚えにくいけど、むちゃ便利なんだ。
たとえば、つぎの二次方程式とかね。
x² – 2x -6 = 0
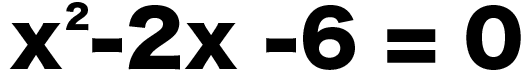
この二次方程式はどうがんばっても、因数分解の公式はつかえない。
たすきがけ因数分解でもかすりもしない。
・・・・・こまった・・・・・・
そんなときは、解の公式の出番だ。
3ステップでとけちゃうよ。
- 解の公式に代入
- √を簡単に
- 約分
二次方程式の係数を公式に代入すると、
x² – 2x -6 = 0
x = 2±√(2² -4×1×-6)/2
= 2±√(4 +24)/2
= 2±√28/2
= 2±2√7/2
= 1±√7
になるね!
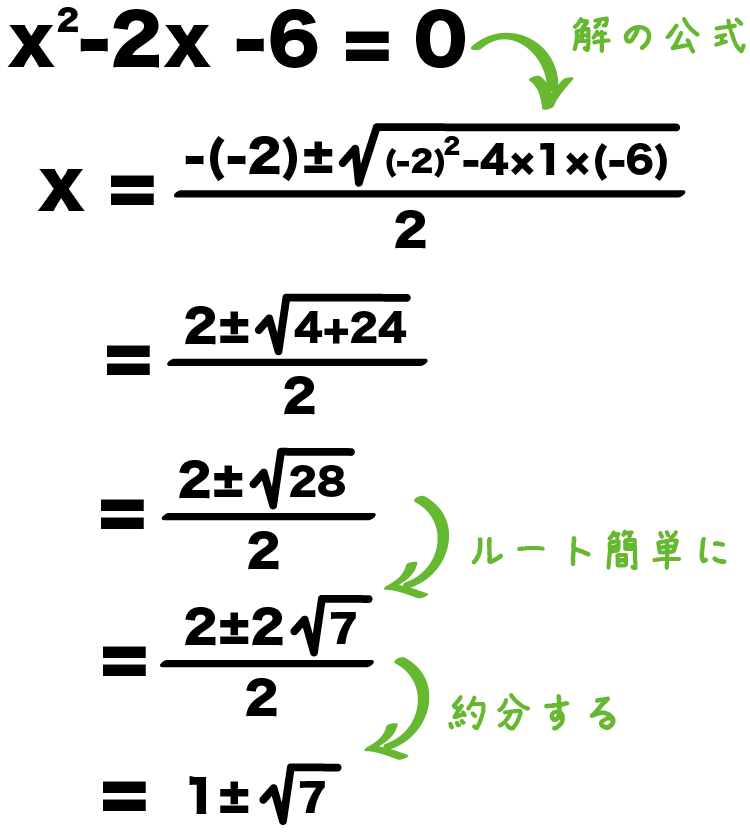
これでどんな二次方程式もとけちゃう!
安心だ〜〜
解き方6. 「平方完成をつかう」
もしも、だよ。
もしも、解の公式を忘れたらどうしたいいんだろう??
因数分解の公式もつかえないし、共通因数でもくくれない。
そんなやばいときに役にたつのが、
平方完成による因数分解の解き方
だ。

平方完成は、解の公式を証明するときにつかった解き方だよ。
だから、解の公式を忘れても、解の公式っぽく二次方程式がとけちゃうのさ。
たとえば、さっきの2次方程式、
x² – 2x -6 = 0
を平方完成でといてみようか。
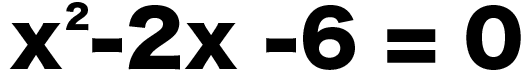
平方完成の解き方は4ステップだよ。
- x以外を右辺に移項
- xをふくむ式の2乗をつくる
- 平方根を求める
- x以外を右辺に移項
この解き方で二次方程式をといてみると、
x² -2x – 6 = 0
x² -2x = 6
x² -2x +1 -1 = 6
(x-1)² = 7
x-1 = ±√7
x = 1 ±√7
になる。

これは解の公式でだした解とおなじ。
解の公式を忘れたときに大活躍だ^^
まとめ:二次方程式の解き方のコツは消去法!
二次方程式の解き方はありすぎる。
どれを使ったらいいかわからないね。
心がけてほしいコツは、
消去法で解き方を選んでいく
ということ。
がつかえるか順番に確認していってね。
きっと、どれかしらで解けるはずだよ。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






X²-5X=6
6を左辺に移項してみて!
4(x+4)^2=25はどうやって計算するんですか??
これは1つ目の平方根の解き方でいけそうだね。
左辺と右辺にルートをつけてみよう。
詳しくは「平方根を使った二次方程式の解き方」を読んでみて
X2+7X-30=0
の場合をお願いします。
これは因数分解の解き方でいけそうだね。
かけたら「-30」、たしたら「7」になる2つの数の組み合わせを考えてみよう!
8X二乗−9=0
教えてください
これは平方根の解き方だね。
-9を右辺に移行してみて!
2(x+2)^= 50
解き方が分かりません
まずは両辺を2で割ってみよう。
あとは平方根の解き方だね
2X2乗=9(X-1)
の解き方を教えて下さい。
2x2乗=9(x-1)
3分の1(4-X)=-2分の1Xの二乗-2
この問題ってどう解けばいいんですか?
右辺の()を外して左辺に移項してみよう!
>3分の1(4-X)=-2分の1Xの二乗-2
分母を払ってみよう。
分母の3と2の最小公倍数を両辺にかければいいのさ!
X二乗-3X-18=0はどうやって解いたらいいんですか?
>X二乗-3X-18=0はどうやって解いたらいいんですか?
因数分解の解き方でいけそうだね。
かけたら「-18」、たしたら「-3」になる2つの数字の組み合わせを考えよう!
x2じょう+x-12=0はなに?
>x2じょう+x-12=0はなに?
因数分解でとけそうだ。
かけて-12、足したら1になる2つの数の組み合わせを考えよう
5X2乗+35X=0
どうやって解くんですか
3分の1エックス(4-X)=2分の1Xの二乗-2
どう計算すればいいですか?
2x²-9xー56=0
解き方教えてください‼
>3分の1エックス(4-X)=2分の1Xの二乗-2
分母を払おう!
分母の3と2の最小公倍数をかけてみて!
>2x²-9xー56=0
これは公式で因数分解できなそうだから、
たすき掛けを使おう
>5X2乗+35X=0
両辺を5で割って式を簡単にしよう。
あとは共通因数を使う解き方でオッケー
3分の1エックス(4-X)=2分の1Xの二乗-2
2X(4-X)=3X二乗-2
8X二乗-2X二乗=3X二乗-2
8X二乗-3X二乗-2X二乗=-2
3X二乗=-2
Xの二乗=-3分の2
ここまでやてみたんですが、このあとが分かりません
どうやるんですか?
>2X(4-X)=3X二乗-2
ここが間違ってるね!-2にも6をかけないとね
6x二乗-7x+2=0
教えてください
6x二乗-7x+2=0
>6x二乗-7x+2=0
因数分解の公式使えなそうだから、
たすき掛けの因数分解だ。
2x^2-4-15x=0
>2x^2-4-15x=0
因数分解できないみたいだから解の公式使ってみて〜
2x2乗+xー6=0
お願いします
2×2乗-3x+3=-2x+18
教えてくださいm(_ _)m
>2x2乗+xー6=0
これは因数分解の公式が使えなそうだから、
たすき掛けで解いていくよ
>2×2乗-3x+3=-2x+18
まずは右辺にあるxの項と整数を左辺に移項して、
同類項をまとめてみよう
(x+2)2+7(x+2)+6=0
の解き方教えてください。(x+2)の後は、二乗です。
>(x+2)2+7(x+2)+6=0
同じ式が2回以上出てきている式は置き換えるのがいいね。
x+2=Aとすると、
A2+7A+6=0
みたいに、Aについての二次方程式ができるね。
これをいつも通りとけばいいんだ。
2X2乗=27Xの解き方がわからない
>2X2乗=27X
27xを左に移項して、共通因数xでくくってみよう!
X(X+5)=126
解き方を書いて教えてください!
>X(X+5)=126
左辺の()を分配法則で展開して126を左辺に移項してみよう!
初めまして。職場で計算問題を部下に教えようと思いましたがそもそも私が解けませんでした。解放をご教授くだされば幸いです…問題 A地点とB地点112kmをボートで往復します。のぼりは7時間下りは4時間かかりました。この川の流れは毎時何kmでしょうか? 宜しくお願いしますm(__)m
>A地点とB地点112kmをボートで往復します。のぼりは7時間下りは4時間かかりました。
この川の流れは毎時何kmでしょうか?
ボートの速さを毎時xkm、川の流れの速さを毎時ykmとしてみましょう。
下りの時は、(川の速さ+ボートの速さ)で進んでいて、
登るときは、(ボートの速さ-川の速さ)で進んでいることがヒントです。
あとは、登りと下りの速さを実際に計算してみて、xとyの連立方程式を作ってみましょう!
4x2乗=25の解き方教えてください!!
>4x2乗=25
まずはxの前の係数の4で両辺を割ってみよう。
そして、あとは平方根の計算でxから2乗をとるだけ
1辺がxcmの正方形の一方の1辺を12cm長くしもう一方の1辺を12cm短くしてできる長方形の面積は12cm²である。
という文から方程式を作るのですが(12+x)(12-x)=12であってますか?
合っていたら解き方を教えてください
Xの2乗+4X=8を教えてください!
>1辺がxcmの正方形の一方の1辺を12cm長くしもう一方の1辺を12cm短くしてできる長方形の面積は12cm²である。
という文から方程式を作るのですが(12+x)(12-x)=12であってますか?
あってるよ!
()を分配法則で外してみよう!
あとは12を左辺に移項して因数分解すればいいんじゃないかな
>Xの2乗+4X=8
因数分解できなそうだから、
解の公式か、平方完成で解いてみよう。
2xの2乗+4x-aの2乗+4=0
の解の1つがaであるときのaの値
x2乗+3x-2分の7=0
途中式と解をよろしくおねがいします。
>2xの2乗+4x-aの2乗+4=0
x=aを代入してaの二次方程式を解こう
>x2乗+3x-2分の7=0
両辺に2をかけて分数を消し去ろう。
因数分解できなそうだったら解の公式で解いてしまおう
√3の整数部分をa、小数部分をbとするとき、aの4乗-bの4乗の値を求めなさい。
文章ですがよろしくお願いします。
X²+6X=5
の問題なんですが、途中式で9が出てくる見たいでなんで9が出てくるのかわからないので、教えて頂きたいです。
xの2乗-x=4
お願いします。
2/3x(5-x)=4の解き方を教えてください
(x-3)(x+3)=8x 教えて下さい。
>√3の整数部分をa、小数部分をbとするとき、aの4乗-bの4乗の値を求めなさい。
文章ですがよろしくお願いします。
まずはaの4乗-bの4乗を因数分解してみよう!
>X²+6X=5
因数分解できないから解の公式か、平方完成で解いてみよう。
9が出てくるのはおそらく平方完成を使ってるね。
>xの2乗-x=4
因数分解できないから、解の公式か平方完成だ!
3X+X-4=0
を教えてください!
>2/3x(5-x)=4
分数があるときは分母を払って
分数を消し去ろう!
>(x-3)(x+3)=8x
左辺を乗法公式で展開して、
8xを左辺に移項してみよう。
あとは因数分解の解き方でいけるはず
>3X+X-4=0
xの項の足し算を計算して、
整数の-4を右辺に移項してみて。
あとはxの係数で両辺を割ればよし
3Xの2条+X-4
をおしえてください!
>3Xの2条+X-4
これはたすき掛けの因数分解でとけそうだね。
xについての二次方程式
x^2-2x-(k+6)=0…[1]
x^2+kx+2k=0…….[2]
(問題)
整数nが、[1]と[2]ね共通の解になるとき、kとnの値を求めよ
この問題教えてください
2x^2-7x+6=0
を解いている過程で、
(2x-3)(x-2)=0という式と、
(-2x+3)(-x+2)=0という式が生まれたのですが、
どちらが正しいでしょうか。
最後の平方完成がわかりません。
なぜ、x² -2x = 6
x² -2x +1 -1 = 6
(x-1)² = 7
x-1 = ±√7
x = 1 ±√7
6を移行して-1を左辺にするのか詳しく教えてください。
>(2x-3)(x-2)=0という式と、
(-2x+3)(-x+2)=0という式が生まれたのですが、
どちらが正しいでしょうか。
どっちも正しいよ!
後者は()の式にそれぞれマイナス1がかけられているだけ
>なぜ、x² -2x = 6
x² -2x +1 -1 = 6
(x-1)² = 7
x-1 = ±√7
x = 1 ±√7
6を移行して-1を左辺にするのか詳しく教えてください。
これは計算しやすくするためだね。
最終的に、
(xの式)2 = 整数
の形に持って行きたいから6を右に移項したよ
200x-8x^2=1200
これどうやって解くんですか
a(1-x/100)b(1+2x/100)
の場合、
ab(1-x/100)(1+2x/100)
になるのですか?かっこの中は関係ないです笑
さっきの問題の続きです
失礼致します。
ab(1-x/100)(1+2x/100)=a×b…(1とします)
【答え】 1+x/100-2x^2/10000=1…….(2とします)
2x^2-100x=0……..(3)
2x(x-50)=0……..(4)
x=0,50
何から何までわかりません…。なぜ(1)から(2)になるのか。なぜ(2)から(3)になるのか。なぜ(3)から(4)になるのか。
できるだけ詳しくお教え下さい。
回答おねがいいたします。
>200x-8x^2=1200
まずは1200を左辺に移項。
あとは、両辺を-8で割って、x2乗の係数を1にしよう!
>a(1-x/100)b(1+2x/100)
の場合、
ab(1-x/100)(1+2x/100)
そうだよ!
>ab(1-x/100)(1+2x/100)=a×b…(1とします)
【答え】 1+x/100-2x^2/10000=1…….(2とします)
2x^2-100x=0……..(3)
2x(x-50)=0……..(4)
x=0,50
1から2へは両辺をabで割ってるね。(ab=0じゃないっていう条件があるはず)
2からは右にある1を左に移項して1を決して、あとはいつも通り、分母をはらってやろう!
1から2へは両辺をabで割ってるね»でも、なぜ
(1-x/100)(1+2x/100)
から
1+x/100-2x^2/10000
のように変化しているんですか?
>1から2へは両辺をabで割ってるね»でも、なぜ
(1-x/100)(1+2x/100)
から
1+x/100-2x^2/10000
のように変化しているんですか?
x/100=Aと置いてみると計算しやすくなるよ
x² -6x+9=0
この問題の解き方を教えてください
>x² -6x+9=0
かけて9、足して-6になる2つの数の組み合わせを考えよう。
「因数分解トレーニング道場」でトレーニングしてみよう
すみません。言い方がまずかったです。
(1-x/100)(1+2x/100)
から
1+x/100-2x^2/10000
になっています。
前者はかっこ付きなのに後者はかっこがないですし、符号が変わっています。なぜですか?
>(1-x/100)(1+2x/100)
から
1+x/100-2x^2/10000
になっています。
()を展開するときは乗法公式を使うか、
公式を忘れたり使えない場合は分配法則を使おう
え
乗法公式使っても答えの通りになりません。
1+(-x/100+2x/100)×1+(-x/100×2x^2/100)
=1+x/100-2x^3/10000
になってしまいます。
-x/100かける2x/100=2x^3/10000ではないですか?
それは答えが間違ってるんじゃないかな笑
すみません
答え間違ってました笑
4x²+x=0 を教えてください
>4x²+x=0
これは共通因数でくくる問題だね。
xでくくってやろう!
何度もすみません
やっぱり、-x/100×2x^2/100=-2x^3/10000
では?
お忙しい所、失礼いたします。
(100-x)^2=8100
100-x=±90
となるのは、なぜでしょうか。
右辺の8100から±90になるのは解りますが、左辺が解りません。
自分勝手ながら、詳しくお願い致します。
失礼いたします。
中学生の内容ではなくて申し訳ないのですが、五角柱以上の角柱の展開図につきまして、
「重なる点」「重なる辺」の問題に弱いです。
立方体なら直角で繋がる辺は重なる、などのウラワザがありますが…。
角柱にもそのようなウラワザはあるのですか?
ないのならば、そういう問題を解くコツを教えて下さい!
問題文を見て、式を作る問題なんですけど
問題1)「大小2つの自然数がある。その差は2で、積は48になる。大小2つの自然数を求めなさい」
と
問題2)「連続した3つの自然数がある。最も小さい数と最も大きい数の積は、真ん中の数の4倍より44大きい。この3つの自然数を求めなさい。」
で、式が分からず、その解き方も分かりません。
ですので、教えてください!
>(100-x)^2=8100
100-x=±90
これは両辺に平方根をつけてるね。
2乗したら(100-x)^2になるのは100-xだからね!
>中学生の内容ではなくて申し訳ないのですが、五角柱以上の角柱の展開図につきまして、
「重なる点」「重なる辺」の問題に弱いです。
この手の問題はむずいよね笑
展開図をかいて地道に消去法で絞ってくのがいいんじゃないかな!
なるほど!
解答ありがとうございました。
やっぱりそうですか…
ありがとうございました!
3(3x+2)^2=1をおしえてください
>大小2つの自然数がある。その差は2で、積は48になる。大小2つの自然数を求めなさい
大きい数をxとしてみよう。
あとは小さい数をxで表して、大小の数をかけたら48になるっていう等式をつくればいいね。
>連続した3つの自然数がある。最も小さい数と最も大きい数の積は、真ん中の数の4倍より44大きい。
この3つの自然数を求めなさい。
真ん中の数をxとして、他の2つの自然数をxで表してみよう。
あとは「最も小さい数と最も大きい数の積は、真ん中の数の4倍より44大きい」を等式にすればいいね
>3(3x+2)^2=1
両辺を3で割って、あとは平方根の解き方で解いてみよう
あ!
思いの外見取り図書くと簡単でした!
本当にありがとうございました!
(t/2+t)×(5+t-5)×1/2=27
これの解き方を順を追って説明お願い致しますm^_^m
>(t/2+t)×(5+t-5)×1/2=27
まずは()の中の足し算を計算。
あとは、両辺に2をかけて分母払ってもいいかもね。
あとはいつも通り二次方程式を解いてくれ
問題1)のほうでその差は”2”とありますが、その”2”はどこで使えばよいのでしょうか?
2回目ですみません
5+(t-5)において、
5+(t-5)
でも、
5-5+t
でも出来ますよね。
計算の順序は、()→×÷→+-
ではないのですか?
>問題1)のほうでその差は”2”とありますが、その”2”はどこで使えばよいのでしょうか?
どっちかの文字をxとしたときに、もう1つの数をxで表すときに使うよ
>計算の順序は、()→×÷→+-
ではないのですか?
その通り!
文章問題の解き方を、分かりやすく教えてください!!!
(x -3)y2+4(3ーx)を、因数分解しなさい。
を、教えて下さい‼️
>文章問題の解き方を、分かりやすく教えてください!!!
方程式の文章題ってことかな?
文章題を作る人の気持ちになってみるといいかな笑
必ず、みんなが解きやすいように、答えとして求めて欲しいものを文字でおくと解きやすく設計されてるね。
時々例外もあるけど!
>(x -3)y2+4(3ーx)
一番後ろの(3-x)にマイナスをつけて、
-(x-3)
にしてやろう。
あとはx-3が共通因数でくくれそうだね!
ややこしかったらA=x-3と置き換えてもいいかな
X2+12x=5 がわかりません
どう解くか教えてください
>X2+12x=5
因数分解できないっぽいから、解の公式か平方完成で解いてみよう
(x+7)²−81=0 の解き方と答えを教えてください。
>(x+7)²−81=0
これは平方根の解き方だね。
81を右辺に移項して、両辺の平方根をとってみよう
(90-X)(240+5X)=23400
>(90-X)(240+5X)=23400
分配法則で()を外してみよう。
あとは23400を左に移項していつも通り解いてみよう。
5(x-3)^2=30
>5(x-3)^2=30
両辺を共通因数5で割って簡単にしよう。
あとは平方根の解き方でとけそうだ
5X^2-11X+6=0
の答えは
11±√1/10
では間違えですか?
>5X^2-11X+6=0
の答えは
11±√1/10
では間違えですか?
あってるよ。ただ、√1は1だから、整数で表せそうだね
(x+3)^2=-3x+45 解き方お願いします
4×2乗+20x+25の場合はどうすればいいのでしょう…
>(x+3)^2=-3x+45
左辺を平方の公式で展開。
あとは、右辺にある細いやつらを左辺に移項しよう。
最後は因数分解でいけるはず
>4×2乗+20x+25
こいつはたすき掛けの因数分解でいけそうだね。
(x-2)2乗=9はどうすれば解けますか?
>(x-2)2乗=9
これは平方根の解き方でいけそうだね。
2乗を両辺からとってみて
X(X-4)=0
>X(X-4)=0
Xか(x-4)のどっちかが0になるはず。
このことから2通りのxの値を求めてみよう
16x2乗=5はどうすれば良いでしょうか?
>16x2乗=5
x2乗の係数16で両辺を割ってみよう。
あとは平方根の解き方でオッケー
xについての二次方程式x^2+4x+a=0の解の1つがx=-6のとき、aの値ともう1つの解を求める方法を教えてください
>xについての二次方程式x^2+4x+a=0の解の1つがx=-6のとき、aの値ともう1つの解を求める方法を教えてください
x=-6を代入してaを求めてみよう。
そのあと、今度はaを代入してxだけの二次方程式を作る。
あとはいつも通り因数分解してといてもう一つの答えを見つけるだけ
(x-1)2乗=15教えて下さい!
x2乗➕3x➖5=0教えて下さい
>(x-1)2乗=15
平方根の解き方でいけそうだね!
>x2乗➕3x➖5=0
因数分解できなそうだから
解の公式を使ってみよう
X2乗 + 2/3 X - 9/4 = 0
はどのようにしてとくのか教えてください
>X2乗 + 2/3 X - 9/4 = 0
分母の最小公倍数をかけて分数を消し去ってみよう
4×2乗=28
の解き方が分かりません
教えてください
x2乗-6x+7=0
>4×2乗=28
平方根の二次方程式だね。まずは両辺を4で割ってみよう。
最後に両辺の平方根を取ってやればいいね
>x2乗-6x+7=0
因数分解できるようでできないから
解の公式を使って解いてみよう
x2乗プラス5xプラス6=0はなんですか?
>x2乗プラス5xプラス6=0
これは因数分解できそうだから因数分解を使った解き方で解いてみよう
2x(x-4)(x+4)-9x=(x-2)²
X2乗ー7=0
>2x(x-4)(x+4)-9x=(x-2)²
これは三次方程式だね。一度全部展開して最後に三乗の公式を使うんでいいんじゃないかな
>X2乗ー7=0
-7を右辺に移行してみよう。
あとは両辺の平方根を取ってやるだけね。
詳しくは「平方根を使った二次方程式の解き方」を読んでみて
X(X-9)=0はどうなりますか?
>X(X-9)=0はどうなりますか?
これは答えの出る直前だね。
Xと(X-9)をかけたら0ってことは、どっちかが0ってこと。
これを求めにxの値を求めてみよう
(3X)2乗=(5Y)2乗 の場合Χは何、Υは何てすか
>(3X)2乗=(5Y)2乗 の場合Χは何、Υは何てすか
まず指数を計算してみよう。
あとはときたい文字の係数で両辺を割ってやるといいよ
x2乗+2x-48の場合、どうすればいいでしょうか?
>x2乗+2x-48の場合、どうすればいいでしょうか?
因数分解の公式を使ってみよう
4×2+10x=0を二次方程式で解くにはどうしたらいいですか??
よんえっくすじじょうたすじゅうえっくす=0です!わかりにくくてごめんなさい
>4×2+10x=0を二次方程式で解くにはどうしたらいいですか??
共通因数でくくる問題だね。
2xで()くくってみようぜ
X2乗+ax+b=0の解き方を教えて下さい。
>X2乗+ax+b=0の解き方を教えて下さい。
解の公式を使おう!
-3分の1X+4=Xの解き方を教えてください!
>-3分の1X+4=X
xの項を左辺、それ以外を右辺に移項してみようぜ
9x²-24x+16=0
の解き方を教えてください!!
>9x²-24x+16=0
の解き方を教えてください!!
因数分解の公式で解けそうだね!
平方の公式を使ってみよう
4x^2-x-3を説明しながら因数分解してください
>4x^2-x-3
こいつはたすき掛けの因数分解だね!
x²+(x+6)²=20 の解き方を教えてください!
>x²+(x+6)²=20
2つ目の項を平方の公式で展開してみよう。
あとは20を左辺に持ってきて見慣れた二次方程式の形にしてやればいいね
解の公式で解いて約分できる時は、して良いですか?
>解の公式で解いて約分できる時は、して良いですか?
いいよ!
(2x+1)2乗=9
の解き方分かりますか???
>(2x+1)2乗=9
こいつは平方根の解き方でいけるね!
36-3(x-3)²=0の解き方ってなんですか?
>36-3(x-3)²=0
こいつは平方根の解き方でいけそうだ。
36を右辺に移項して、両辺を-3で割って最後に両辺の平方根をとってみよう
Ken先生の解説いつもわかりやすい!
いつもありがとう!
ありがとう!!
ボールを投げて秒速30mで真上に投げるとき、投げてからx秒後のボールの高さは、およそ(30x-5xの2条)mである。ボールの高さが40mになるのは投げてから何秒後ですか。
(18-x)(27-x)=400の解き方を教えてください。
>ボールを投げて秒速30mで真上に投げるとき、投げてからx秒後のボールの高さは、およそ(30x-5xの2条)mである。ボールの高さが40mになるのは投げてから何秒後ですか。
xで表したx秒後のボールの高さ=40m
という二次方程式を作ろうぜ
>(18-x)(27-x)=400の解き方を教えてください。
(18-x)(27-x)を展開して、400を右辺に移項して因数分解してみよう!
3(xの二乗ー8)=(xー8)(x+2)
この解き方を教えて下さい!!!
>3(xの二乗ー8)=(xー8)(x+2)
これは一回全部展開しちゃおう。
3(xの二乗ー8)は分配法則で、(xー8)(x+2)は乗法の公式で。
で、あとは移項なりなんなりで整えていつものように二次方程式を解いてみよう
ありがとうございます‼️
平行完成と解の公式は
どんな時に使えばいいのかいまいちよくわかりません。
すみませんが、教えて下さい!!
>平行完成と解の公式は
どんな時に使えばいいのかいまいちよくわかりません。
因数分解できない、共通因数でくくれない、もう無理・・・・・
ってなった時に解の公式を使おう。
で、平方完成は解の公式を忘れてしまった時に使おうw
解の公式を使った時に、分母の√内が負になった場合はどうすれば良いのでしょうか?
ルート中身が負の数になった数を「虚数」というんだけど、これをiで表すことになるよ。
ただ、虚数は高校数学の範囲なので、計算ミスを疑ってみよう!
分かり易かったです!ありがとうございます!
食塩水の2次方程式応用文章題に困っています。何について立式したらいいのか、何をXでおけばいいのかを教えて頂きたいです
問題にもよるけど、困ったら文章題で求めたいものをXでおけばいいよ〜
だいたい問題がそう設計されている
(X+1)(x―3)=3x+3
がよくわかりません
まずは左辺を乗法公式で展開してみよう。
そのあとに右辺を左辺に移項してやればいいね
2x²-3=0という問題を解いていました。前にYouTubeで見たある勉強動画では、計算した答えで√の中に分数が入っていたら最後に有理化をして答えを出していたのですが、私がさっきやった練習プリントの答えは有理化をせずに+-√分数のままが答えでした。
これはどういうことですか??
(ちなみに、分母の数は4、とか9とか二乗にはなってません。)
どっちでもいいけど有理化しておいたほうが無難だな〜
完全平方式を作って、
4xの2乗+3x-2=0
が、分からないです。
まずは数字の項を右辺に移項して
左辺を4でくくってみようぜ
3x二乗➕2x=0
の解き方と答えを教えてください
xっていう共通因数でくくってやろう〜!
ありがとうございました!!!!!!!!!!!!!!
(x+1)(x-3)= -4(x-1)
の解き方が、わかりません。
教えていただけませんでしょうか?
よろしくお願いします。
x二乗-7=0の答えがx=±√7になる理由を教えてください。
(x-9)2乗=25
この式はどうしたら解けますか??