平方根をつかった二次方程式の解き方の3つのステップ

平方根をつかった二次方程式の解き方？？

こんにちは！この記事をかいてるKenだよ。天にのぼりたいね。

二次方程式の解き方にはいろいろある。

因数分解の公式をつかったり、

共通因数でくくってみたり、

解の公式をつかったり、

たすきがけの因数分解をつかってみたり、、、、

と大忙しだ。

ぶっちゃけ、どの解き方を使えばいいかわからんよね？？

今日は、もう1つ新しい2次方程式の解き方を紹介するよ。

その名も、

平方根をつかった二次方程式の解き方だ。

2次方程式の基礎だから、しっかりおさえておこうね。

平方根をつかった二次方程式の解き方がわかる4ステップ

さっそく、平方根をつかった解き方を紹介していくよ。

つぎの練習問題をといてみよう。

練習問題

つぎの二次方程式を解きなさい。

（x-2）^2 -48 = 0

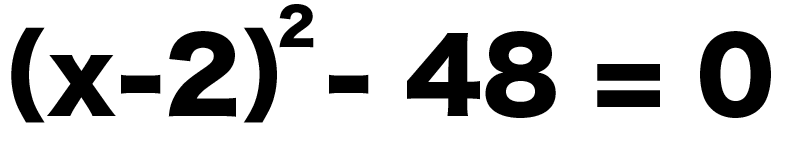
Step1. 移項する

「（）の2乗」以外を右辺に移項しちゃおう。

例題でいうと、

48

が（）の2乗以外の項だね。

こいつを右辺に移項してやると、

（x-2）^2 -48 = 0

（x-2）^2 = 48

になるね。

Step2. 二乗をとる

つぎは左辺の2乗をとってみよう。

左辺の2乗をとるだけじゃなくて、その分、右辺を「左辺の平方根」にしてあげてね。

つまり、

右辺に±とルートをつければいいのさ。

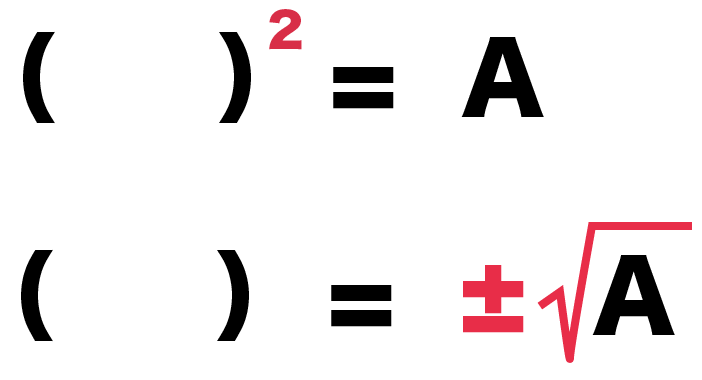
練習問題でもおなじ。

左辺の2乗をとって、右辺を「左辺の平方根」にしてやると、

（x-2）^2 = 48

（x-2）= ±√48

になるね。

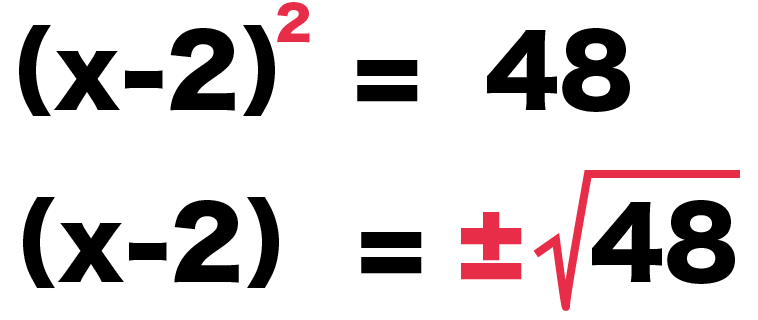
Step3. 移項する

つぎはx以外を右辺に移項しよう。

最終的に「x＝」にもっていきたいからね。

練習問題の左辺には、

-2

っていうx以外の項が残ってるね。

こいつを右辺に移項すると、

（x-2）= ±√48

x =  2±√48

になる。

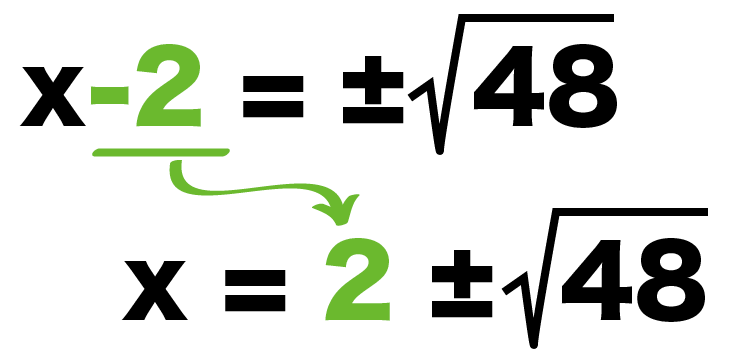
Step4. ルートを簡単にする

最後にルートを簡単にしてあげよう。

ルートの中身の「2乗の因数」を外にだせばいいんだったね？？

やんなくても間違いじゃないけど、

やったほうが計算の余地が確認できてスッキリするよ。

練習問題のルートの、

±√48

に注目してみて。

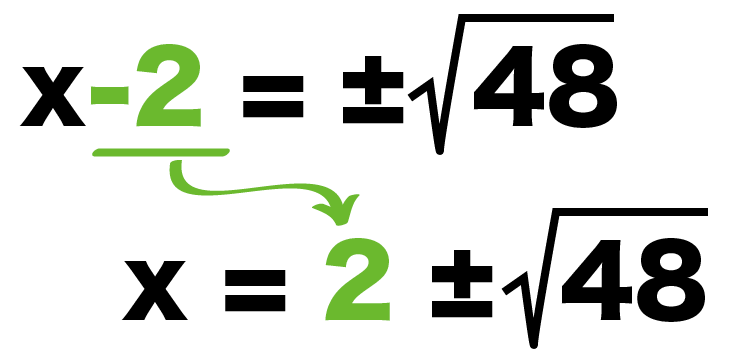
ルートのなかの「48」を素因数分解してみると、

48 = 2×2×2×2×3

になるよね？？

ってことは、

2の2乗（4のこと）

を√の外にとりだせそうだ。

さっそく、√48を簡単にしてやると、

x =  2±√48

x =  2 ± 4√3

になるね。

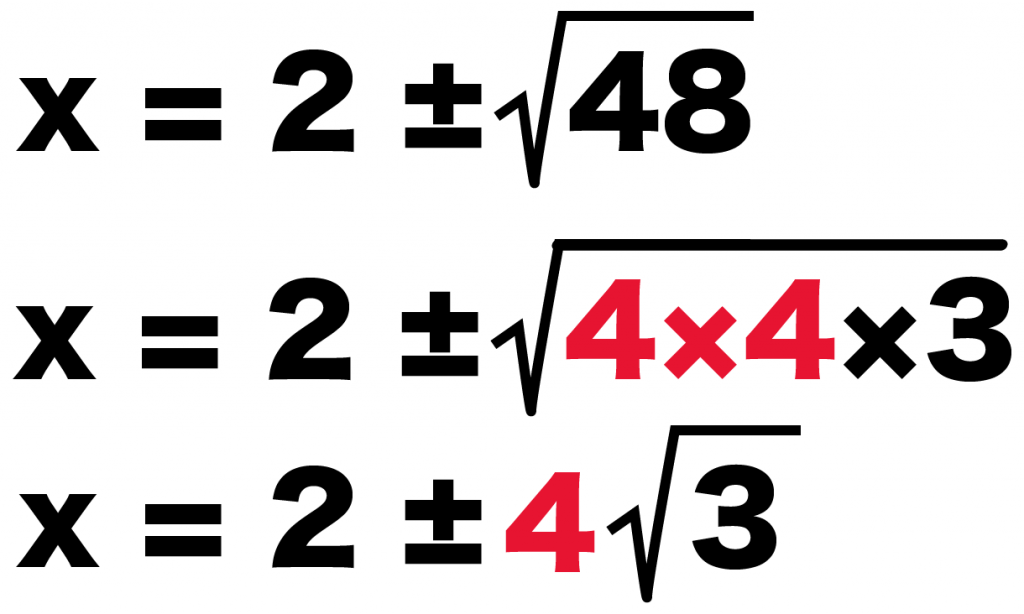
これで二次方程式がとけちゃったんだ。

平方根をつかうと簡単に解けるね。

まとめ：平方根をつかった二次方程式の解き方は移項しまくれ！

平方根をつかった二次方程式は4ステップでとけちゃうよ。

1. 移項
2. 二乗をとる
3. 移項
4. ルートを簡単にする

みたかんじ、移項できればとけそう。

ガンガン平方根をつかっていこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。