【二次方程式】解の公式の証明がわかる4つのステップ

二次方程式の解の公式を証明したい？？

2次方程式に悩んでいるみんな、こんにちは！犬飼ふゆだよ。

解の公式はむちゃくちゃ強い味方。

どんな二次方程式もとけちゃうからね。

でも、

どうして解の公式なんてあるの？

とか、

覚えづらいよ！

とか、

なんで解の公式ができたんだろう？？

って疑問におもうよね。

だから、今日は、

解の公式がなぜ使えるのかを証明したいんだ。

ややこしいけど、give upしないでついてきて欲しいなぁ。

= もくじ =

1. 解の公式とはなんだっけ？？
2. 展開の公式の復習
3. 解の公式の証明の4ステップ

解の公式とはなんだっけ？？？

まず、解の公式を思い出してみよう。

二次方程式の「ax^2 + bx + c = 0」があったとすると、

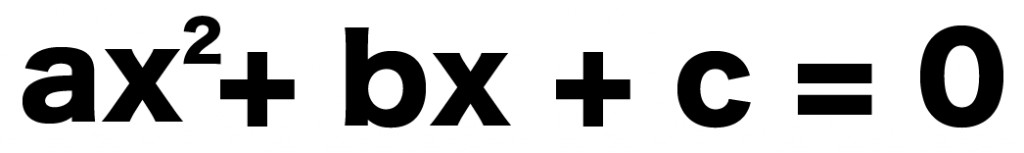
解のxは、

x = {-b±√(b^2 -4ac)}÷2a

であらわせるんだったね？？

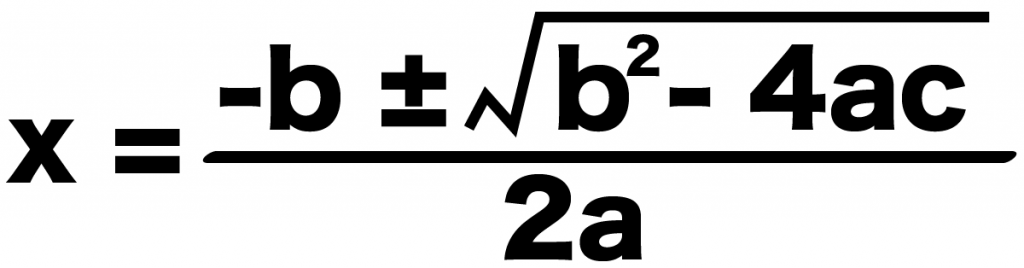
⇒ 解の公式をつかった二次方程式の解き方はコレ読んでね^^

どんな二次方程式でもとけちゃう。複雑だけど便利なんだ。

解の公式の証明がわかる4つのステップ

解の公式を証明してみるよー。

むずかしめだけど、ついてきて欲しいなあ。

証明のゴールは、

二次方程式「ax^2 + bx + c = 0」

を

x ={-b±√(b^2 -4ac)}÷2a

に変型することだよ。

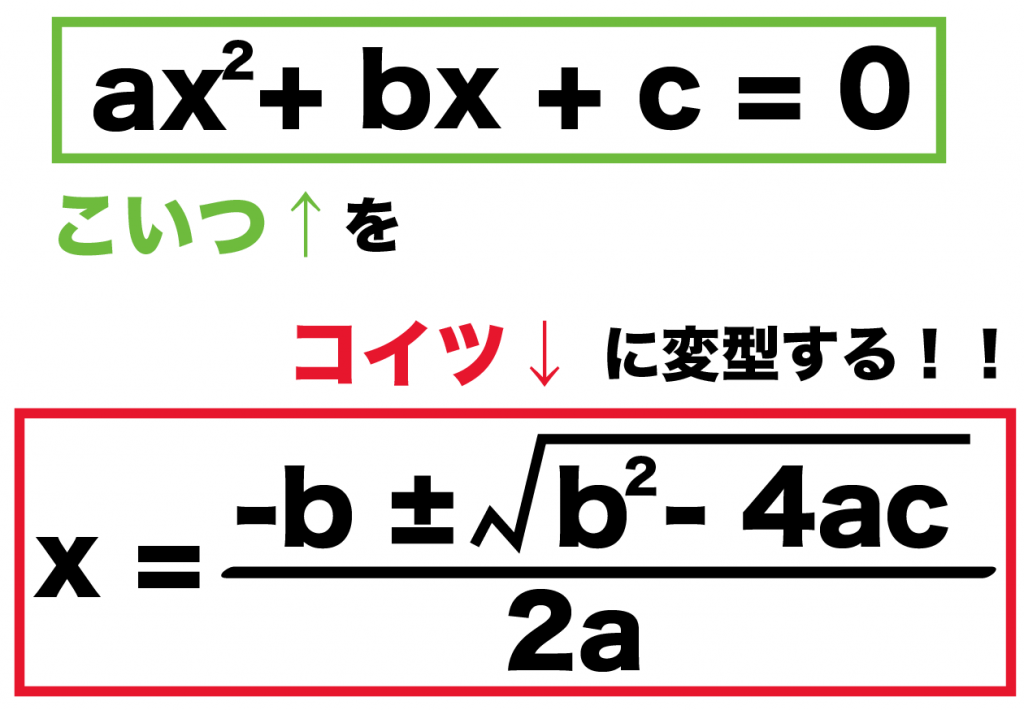
証明のゴールはみえたかな？？

さっそく証明していこう。

Step1. 「x2をシンプルにする」

x2をシンプルにしよう。係数を1にするってことだね。

そのために、

二次方程式「ax^2 + bx + c = 0」の両辺をaで割ればいいんだ。

x2だけじゃなく「bx+c」もaで割ってね。

さっそく、計算してみると、

ax^2 + bx + c = 0

x^2 + b/a x + c/a = 0

になる。

Step2. 「xの係数の半分を２乗したもの」を足して引く

つぎはxの係数に注目してね。

なんと、

「xの係数の半分を2乗したもの」を足して、そして引くんだ笑

意味不明だけどやってみて。

二次方程式「ax^2 + bx + c = 0」は、

x^2 + b/a x + c/a = 0

になってたよね？？

ってことは、xの係数は「b/a」だ。

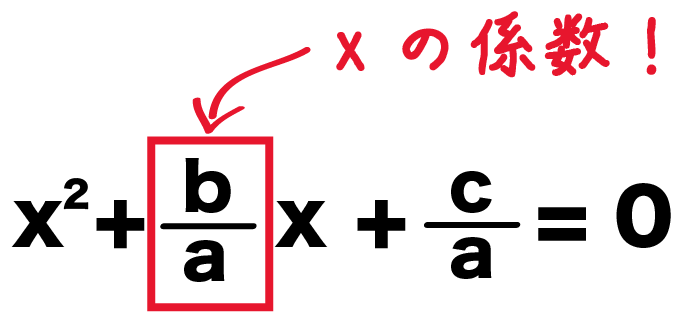
こいつを半分にして2乗した「（b/2a）の2乗」を足して引いてあげるんだ。

すると、

x^2 + (b/a) x + c/a = 0

x^2 + (b/a) x+ (b/2a)^2 – (b/2a)^2 + c/a = 0

になるね！

Step3. 「（　）２＝　　という形を作る」

「（　）の2乗という形」をつくるよ。

どうして（　）２＝という形かっていうと、

ｘ= ○○ にもっていきたいからだよ。

さっきのステップでは、

xの係数の半分の2乗をたしてひく

をしたよね？？

じつはこれ、

「 (　)2 =　　という形」を作るためだったんだ。

さっきの計算式に注目してみて。

x^2 + (b/a) x+ (b/2a)^2 – (b/2a)^2 + c/a = 0

のうち、3つの項の「x^2 + (b/a) x+ (b/a)^2 」を公式で因数分解すると、

x^2 + (b/a) x+ (b/2a)^2– (b/2a)^2 + c/a = 0

（x + b/2a）^2 –  (b/2a)^2 + c/a = 0

になるね。

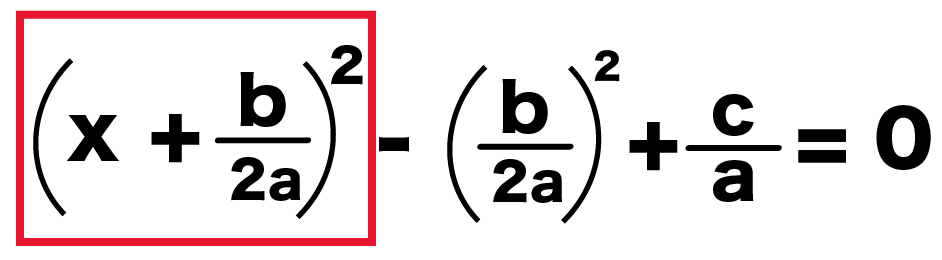
「（x + b/2a ）の2乗」以外の項の、

• -（b/2a）の2乗
• c/a

を右に移項してやると、

（x + b/2a）^2 =  (b/2a)^2 – c/a

になる。

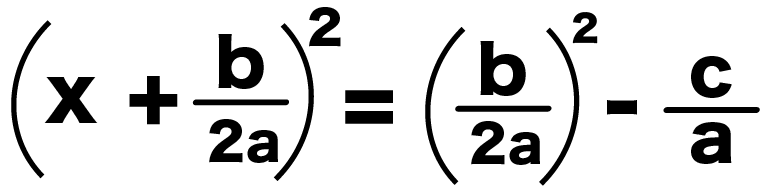
これで、

「(　)2 =　　という形」がつくれたね^^

Step4. 右辺をまとめよう

移項した右辺をまとめよう！

1つの分数にすればいいわけだ。

(b/2a)^2の指数をはずすと、

（x + b/2a）^2 =  (b/2a)^2 – c/a

（x + b/2a）^2 =  b^2/4a^2 – c/a

になるね。

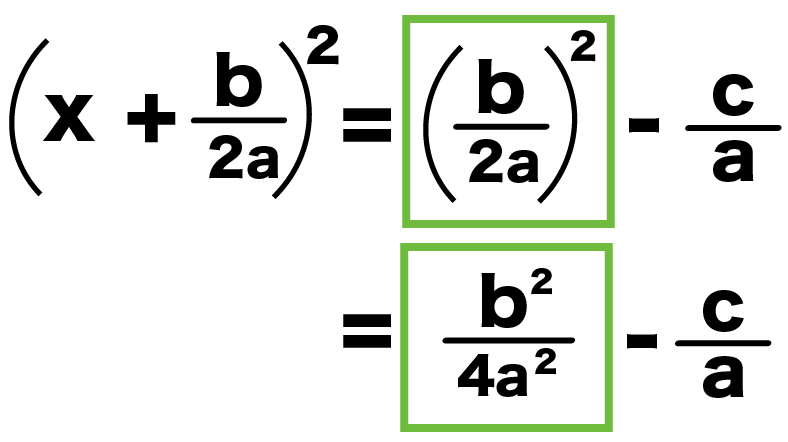
つぎは、2つの分数を通分すると、

（x + b/2a）^2 =  b^2/4a^2 – c/a

（x + b/2a）^2 =  (b^2 -c×4a)/4a^2 

（x + b/2a）^2 =  (b^2 -4ac)/4a^2 

になるね！

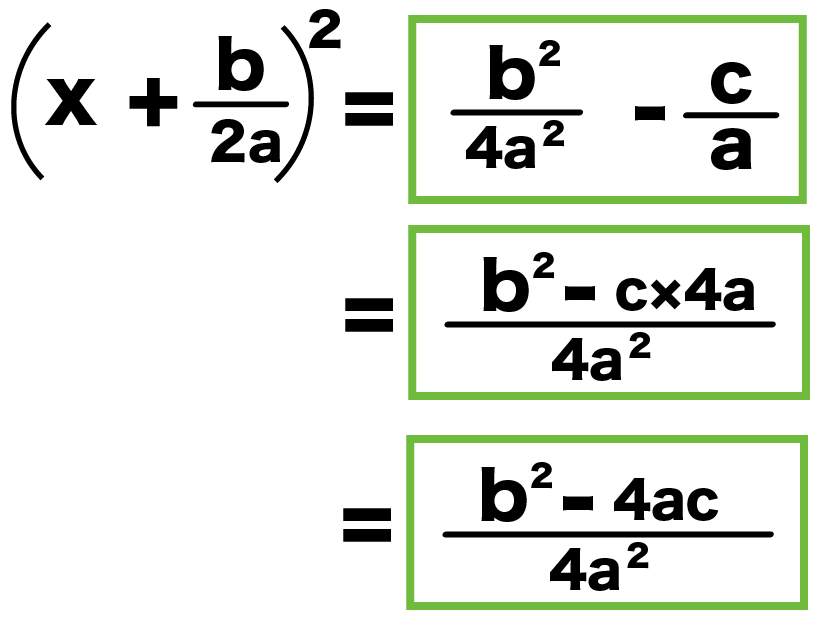
Step5. 両辺をルートしてみよっか？

最終的に「ｘ＝　」という形にしたいから、(　)2 がいらないね？

両辺をルートしてみよう。

すると、

√{（x + b/2a）^2}  = √{ (b^2 -4ac)/4a^2 }

になる。

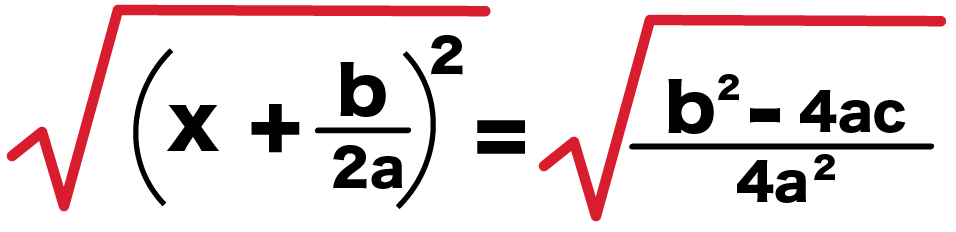
√をそれぞれはずしてやると、

x + b/2a  = ± (b^2 -4ac)/2a

になるよね？

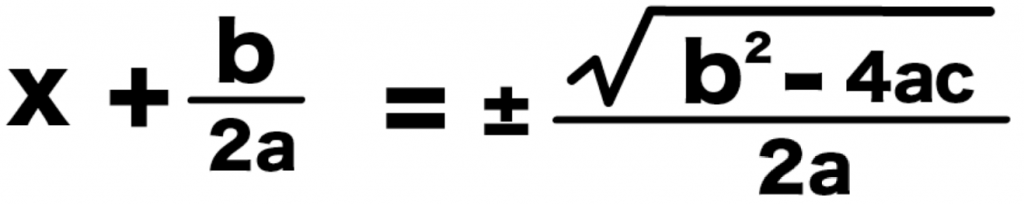
解のxを求めたいから、左辺の「b/2a」を移項してやると、

x = -b/2a ± (b^2 -4ac)/2a

になる。

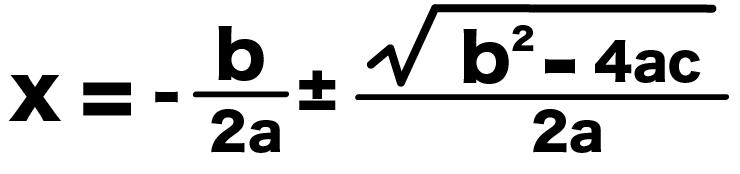
これをまとめると、

x = {-b± (b^2 -4ac)}/2a

になるね！

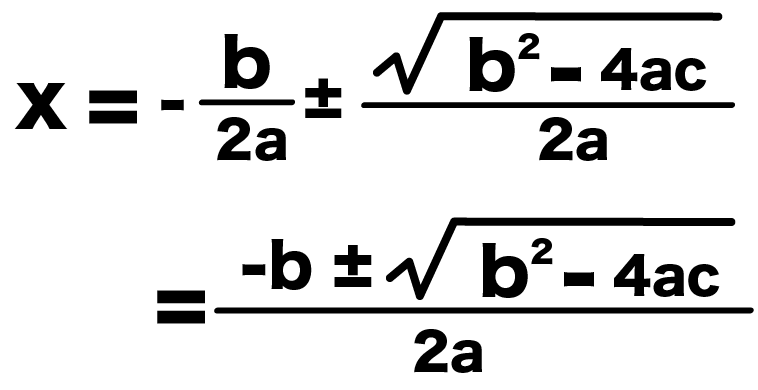
これで解の公式の、

x = {-b±√(b^2 -4ac)}÷2a

が導けたね^^

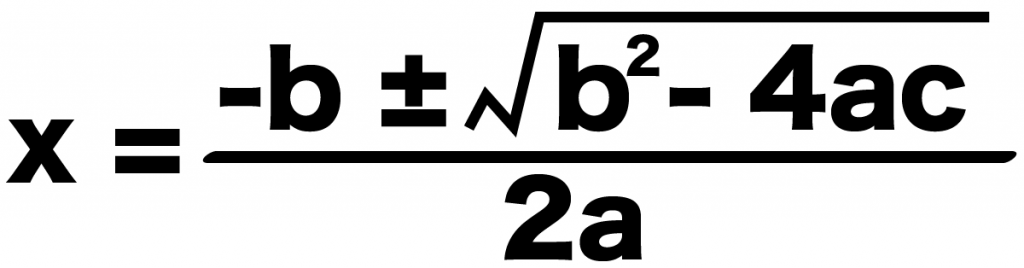
2次方程式の解の公式の証明はながい笑

二次方程式の解の公式の証明はどうだった？？

いきなり覚えろって言われても納得できないよ

　って人や、

解の公式の謎を知りたい

って人のために書いてみたー。

わかるまで何回も証明してみてね。

そんじゃねー

犬飼ふゆ