二等辺三角形の定理の証明がわかる3ステップ

二等辺三角形の定理を証明したいんだけど！

こんにちは！この記事をかいているKenだよ。スープは濃いめに限るね。

二等辺三角形の定理にはつぎの2つがあるよ。

1. 底角は等しい
2. 頂角の二等分線は底辺を垂直に2等分する

こいつらって、むちゃくちゃ便利。

証明で自由に使っていいんだ。

でもでも、でも。

疑い深いやつはこう思うはず。

なぜ、二等辺三角形の定理を使っていんだろう？？

ってね。

そんな疑問を解消するために、

二等辺三角形の定理を証明していこう！

二等辺三角形の定理の証明がわかる3ステップ

つぎの、

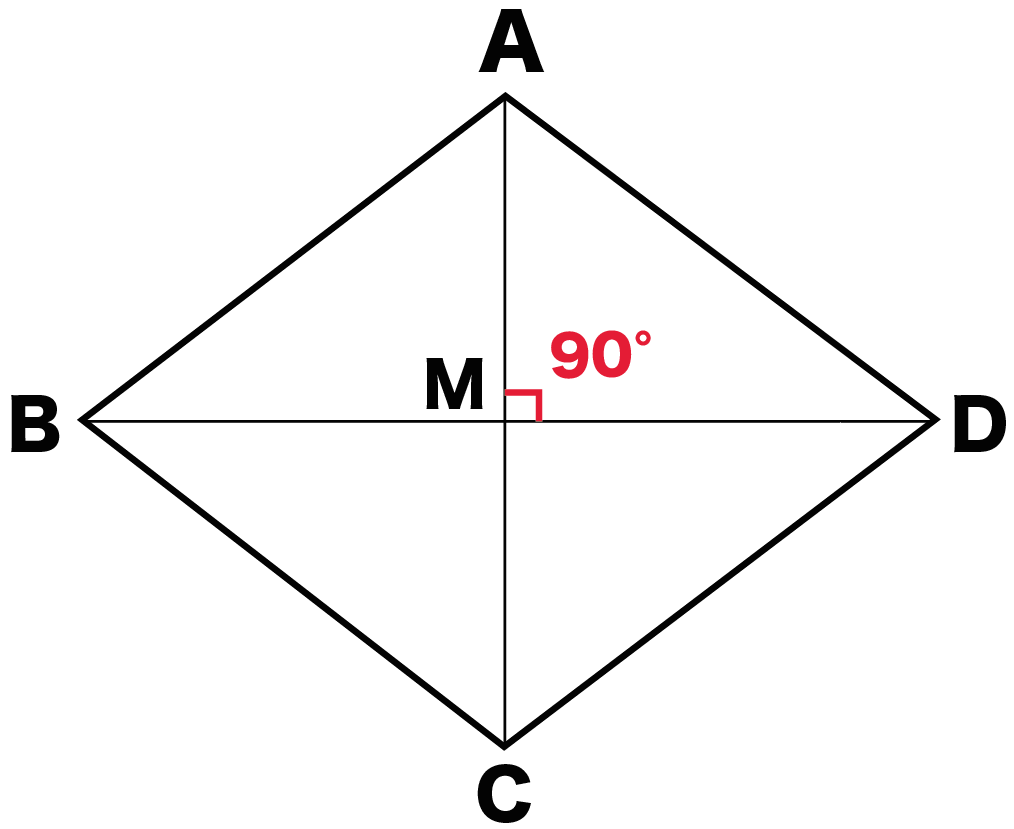
二等辺三角形ABCで証明していくよ。

AB = ACのやつね。

3つのステップで証明できちゃうんだ。

Step1. 頂角から底辺に二等分線をひく！

頂角から底辺に二等分線をひこう。

例題でいうと、

Aの二等分線を底辺BCにひいてやればいいんだ。

底辺との交点をHとするよ。

Step2. 三角形の合同を証明する！

三角形の合同を証明していくよ。

例題でいうと、

• △ABH
• △ACH

の2つだね。

△ABHと△ACHにおいて、

仮定より、

AB = AC・・・(1)

AHは角Aの二等分線だから、

角BAH = 角CAH・・・(2)

辺AHは共通だから、

AH = AH・・・(3)

(1)・(2)・(3)より、

2組の辺とその間の角がそれぞれ等しいので、

△ABH ≡ △ACH

である。

これで2つの三角形の合同がいえたね！

Step3. 合同な図形の性質をつかう！

あとは、

合同な図形の性質、

• 対応する線分の長さは等しい
• 対応する角の大きさは等しい

をつかうだけ！

合同な図形同士の対応する角は等しいので、

角ABH = 角ACH

だ。

こいつらは底角だから、

二等辺三角形の底角が等しい

ってことを証明できたね。

また、対応する角が等しいから、

角AHB = 角CHB

でもあるはずだ。

角AHB と角CHBはあわせて一直線になっている。

つまり、

角AHB + 角CHB = 180°

だね？

ってことは、

角AHB = 角CHB = 90°・・・(4)

であるはずさ。

対応する辺も等しいので、

BH = CH・・・(5)

だよ。

ってことは、

二等分線AHは底辺BCの垂直二等分線

になっている！

つまり、

頂角の二等分線は底辺を垂直に二等分する

ってことがわかったね^^

まとめ：二等辺三角形の定理の証明は合同の性質から！

二等辺三角形の定理は便利。

ぜんぶ、

合同な三角形の性質からきているんだ。

暗記するのも大事だけど、

なぜ、二等辺三角形の定理がつかえるのか？？

ということを知っておいてね^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。