中学数学で勉強する「関数」とはいったい何者???
こんにちは、チャーシュー麺が好きなKenだよ。今日も一緒に中学数学を勉強していこう!!
中1数学の「変化と対応」っていう単元に入ると、
関数(かんすう)
って言葉がでてくるよね??

これは小学校の算数でも出てこなかった奴だね。ちょっと強そうだけど怖そう??笑
今日はこの「関数」とはなにか??っていうことを勉強していくよ。
授業で習った「関数の意味」にイマイチピンときてないキミ! よかったら参考にしてね^^
「関数とは」なにかをWikipediaで調べる。
関数とはいったい何者なんだろうか??
その正体をつかむためにオンライン百科事典のWikipediaで調べてみよう。
コチラのページによると、関数とは、
数の集合に値をとる写像の一種である
って書いてあるね。
はじめて関数に触れる奴にとって、この意味はむずかしすぎない??笑 何回読み返してもよくわからない!!
このページにも書いてあるけど、じつは、
関数って自動販売機にたとえると分かりやすくなるんだ。

ちょっとみてみよう!!
関数とは「自動販売機」だって?!?
関数とは自動販売機である!!
って自信満々にいってみたけど、いったい関数のどこが自動販売機っぽいんだろうか??
この真相をさぐるために、自動販売機のしくみをちょっと復習してみよう。

キミは自動販売機でジュースを買いたいとき、まず何をする??
そう、お金をいれるはずだ。
じゃあ自動販売機にお金をいれたらどうなる???
そう、ジュースが出てくるはずだ。
つまり、自動販売機の中で起こっていることって、
お金をジュースに変えた
ってことなんだ。
そして、自動販売機にはもう1つ特性がある。
それは、
入れたお金によって出てくるものが違う
ということだ。
たとえば100円のジュースを買いたいとしよう。

このとき、自動販売機に100円をいれてボタンを押してやれば、
「100円ジュース」がガシャコっとでてくるはず。
つぎに、いれるお金を変えて500円玉をいれたとしよう。
すると、
今度はチャリチャリとガシャコっていう音ともに、
「400円のおつり」と「100円のジュース」の2つがでてくるよね??
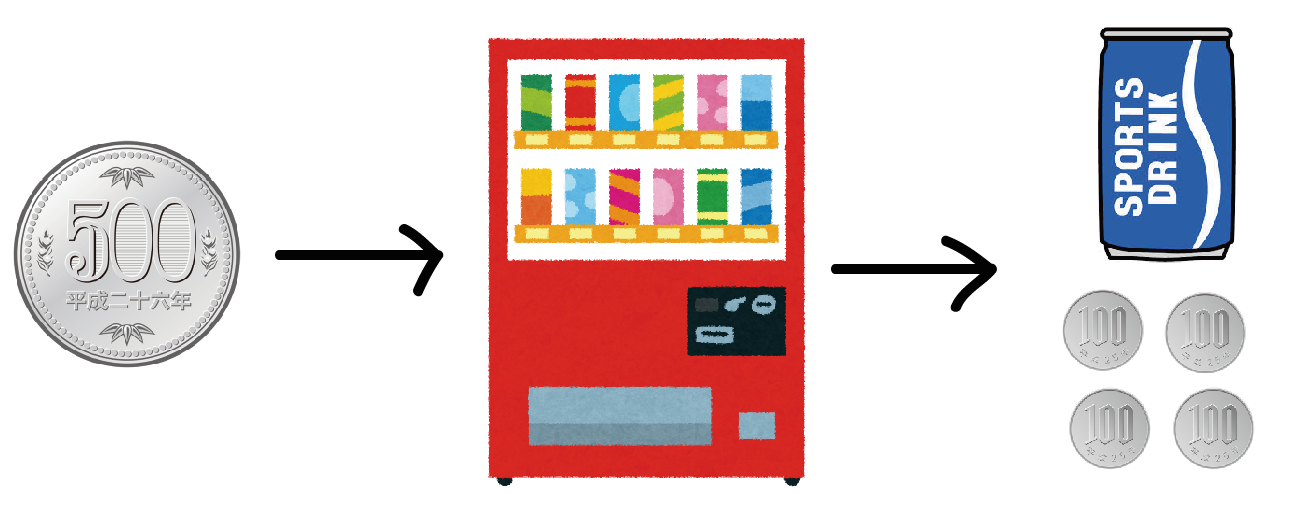
つまり、
自動販売機に何を入れるかによって、でてくるものが違う!
ってことが言えるんだ。ね??そうでしょ??
関数も自動販売機といっしょ!!
関数もこれと同じ。
ある関数に「A」という値をいれてあげたら「B」が出てくるんだ。

なんだろう、たとえるなら手品のマジックボックスだね。鳩をいれたら人間になる、みたいな箱あるでしょ?? あれあれ。
つまり、
何かをぶち込んだら何かがでてくるマシーンみたいなもの
が関数だと思っていいよ。
で、ひとつ気づくのは、
関数に何を入れるかによって、出てくるものが違う
ってこと。
自動販売機でも100円玉のときと500円玉のときでは出てくるものが違ったでしょ?? あれと同じさ。
Cを入れたらDがでてくるんだ。Bじゃない。

よーくみると、
関数に「入れるもの」と「出てくるもの」は変化しているね?? AをいれたらBがでてくるし、CをいれたらDが出てくるっていう感じで。
だから、数学では、
この「入れるもの」と「出てくるもの」を「変数(へんすう)」って呼んでいるんだ。

そんで、中学校で勉強する関数はほとんど、っていうか、たぶん全部が、
Aを「x」、Bを「y」としている。

つまり、xに何かを入れたらyっていうものが出てきましたよ!っていう関数ばかりだということ。
このとき、数学では、
yはxの関数である
というんだ。

ちょっとカッコイイから覚えておこう!!
中学数学で習う「関数」の例!
xの関数であるyの具体例を紹介しよう。
中学1年生では、
y = 2 x
のようなシンプルな関数が登場するよ。
この関数のxに数字の「2」を入れてあげるとyの値は「4」になるし、
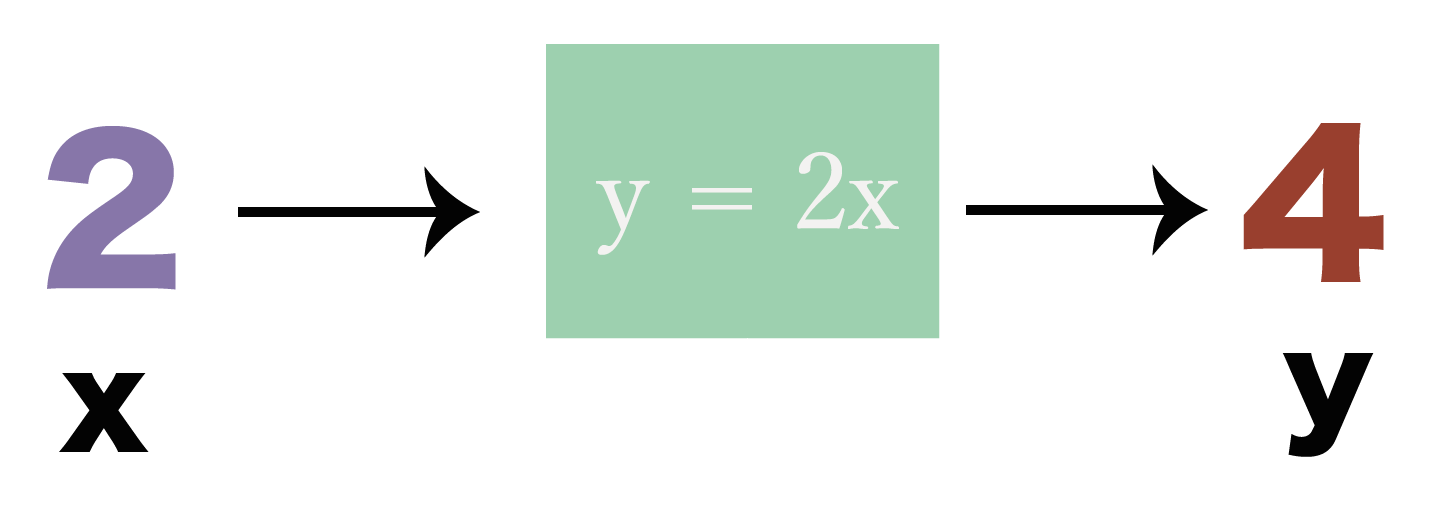
xに「3」を入れると、yは「6」になるね。
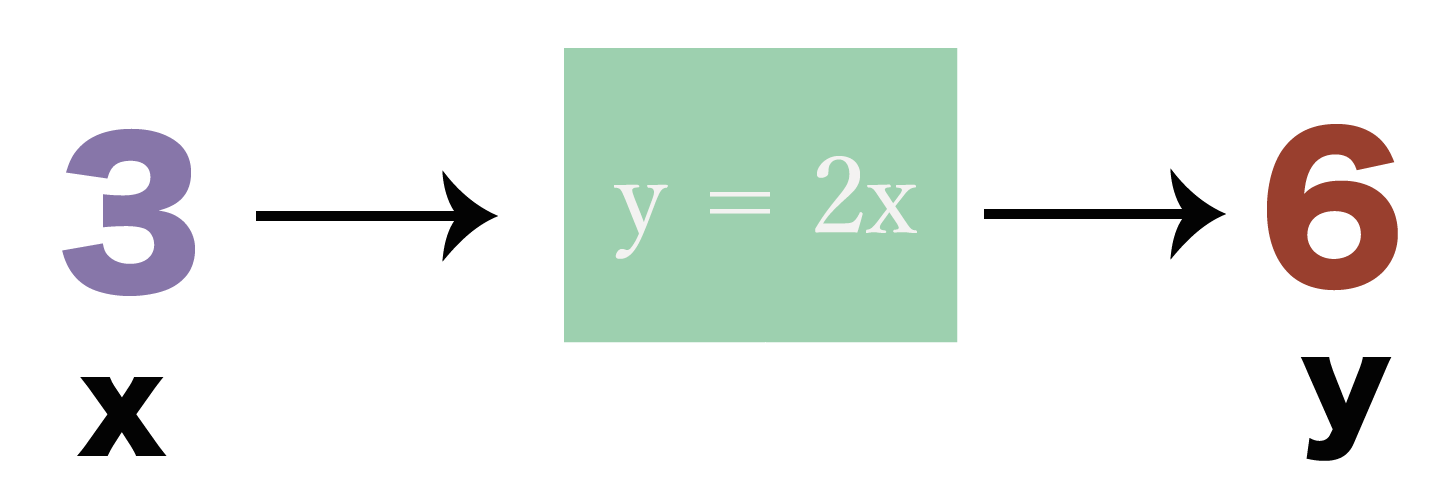
xに何をぶち込むかによって、yの値がちがう。
これが関数さ。
これからゆっくりと中学1年生で勉強する関数の単元をみていこうね^^
そんじゃねー!!
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。


























結構比例や
反比例のことで頭抱えてるんです
もう少し噛み砕いて教えてくれませんか?
特に
①YはXに比例しX=4のときY=-20である
YをXの式で表しなさい
答え、Y=-5
はわかるんですけど
②X=-7のときのYの値を求めなさい
ってなってここが解けなくて答えを見たんですよ
そしたら①の答えのY=-5が関係していて
なんでY=-5が関係するのですか?
教えて下さい!!
まずは1番でyとxから比例定数を出してみよう!
y=axの形で表してみて
質問なんですけど、問題集に【ある数の絶対値をyとする時、yはxの関数ですか? また、xは、yの、関数ですか?】という問題がありどういう風に考えればいいのか、わからないのですけど教えてくれませんか? よろしくお願いします!
xが変化した時、yも変化すると関数だ!
一次関数をこんな感じにわかりやすく(おもしろく笑)教えて欲しいです
ありがとう!笑
一次関数については「一次関数とは」を読んでみてね!
すごく分かりやすいです。
勉強の参考にさせていただきます‼
関数の文章題で少しつまずいてしまうことがあるんですが、かんたんな解き方ってありますか?なければいいんですが教えてくれると幸いです。よろしくお願いします
関数の最大値と最小値ってなんですか?
教えてください!
>関数の文章題で少しつまずいてしまうことがあるんですが、かんたんな解き方ってありますか?なければいいんですが教えてくれると幸いです。よろしくお願いします
具体的にどういう問題かな?
送ってみて!
>関数の最大値と最小値ってなんですか?
変域のことかな!
xがある範囲の値しか取れないとき、yの一番小さい値と大きい値のこと
2つ質問させてください。
(1)「y=0×x+3 は関数ではない。なぜなら、xに何を入れても、出てくるyは3になるから。」という理解で正しいでしょうか??
(2) 「xの約数のうち最大のものをyとする」というとき、yはxの関数でしょうか??
自販機のところが関数でyは変数とありますが、ではなぜ、「yはxの関数である」となるのでしょうか?yは変数でもありますが、xに対しては関数ということなのでしょうか?
今まで中学生の勉強が難し過ぎてついて行けずわからないとこが多かったのですがこのサイトを見つけたおかげで本当にわからないところも解けるようになりました!
本当にありがとうございます!
これからも参考にさせてください!
よろしくお願いします
ありがとう!!励みになるぜ!!
中学2年です。今まで遊びあるってましたがもう二学期。そろそろ勉強しないと高校行けなくなるので…てかもう遅いかもしれないけど頑張って勉強してます、、でも分からないことがありすぎて困ってるときこのサイトに助けてもらってます!これからもよろしくお願いします!
ありがとう!!^^
頑張ろうぜ!!
私は中学一年生です❗私の学校は二学期の学校なので最近後期に入ったばっかなのですが、前期のテスト2回とも200人中95番とかそのくらいのバカなんですがkenさんは、どんな勉強方法をしていますか?
すみませんが教えてください
私は、新体操をしていてオリンピックを目指して1日5時から9時までで、休みの日は9時から9時の練習なのでほとんど休みの日はありません。ですので塾にもいってないです。そんなときはどーいった勉強方法をすればいいですか?
>私は中学一年生です❗私の学校は二学期の学校なので最近後期に入ったばっかなのですが、前期のテスト2回とも200人中95番とかそのくらいのバカなんですがkenさんは、どんな勉強方法をしていますか?
順位はあくまで相対的なものだから、そんな卑下しなくていいんじゃないかな。
必ず勉強でインプットしたら、文章を書いてまとめたり、実際にその知識を使ったりしてアウトプットするようにしてるよ
>私は、新体操をしていてオリンピックを目指して1日5時から9時までで、休みの日は9時から9時の練習なのでほとんど休みの日はありません。ですので塾にもいってないです。そんなときはどーいった勉強方法をすればいいですか?
新体操に振り切ってもいいんじゃないかな!
ただ、授業の時間はみんなと平等に机に座ってると思うから、その時間を有効に使うしかないね。
先生の話を聞いてもいいし、自分で勉強しちゃってもいいと思う
姉の身長がxセンチメートルで、妹の身長がyセンチメートル
これが関数出ない理由を説明しなさい
この問題が何度やっても意味がわからないなどと言われますどのようにして書けばいいのでしょうか?
>姉の身長がxセンチメートルで、妹の身長がyセンチメートル
これが関数出ない理由を説明しなさい
xが変化することで、yが影響を受けるかどうかをみてみればいいね。
姉がいくら大きくなっても、妹は妹。
妹の身長は姉の身長によって変化しないはずだ
質問なんですけど、
四隅から一辺がXcmの正方形を切り取って箱を作る時、箱の底面積をycmとします。
この時、Xとyの変化のようすを表に表しなさい。なお、もとの正方形の一辺の長さは
16センチとする。これが全然分かりません。明日までに返信してくれると嬉しいです
>四隅から一辺がXcmの正方形を切り取って箱を作る時、箱の底面積をycmとします。
この時、Xとyの変化のようすを表に表しなさい。なお、もとの正方形の一辺の長さは
16センチとする
底面積は長方形になるよね?
ってことは、
たてx横
で面積が求められるから、たてと横の長さをxで表してやればいいね!
何を見ても証明の解き方がわかりません!!!
どうすればよいですか??
>何を見ても証明の解き方がわかりません!!!
どうすればよいですか??
証明は初めてだと難しい!ただ、問題を解くうちに書き方がわかってくるはず。
あとは、合同条件とかその他諸々の図形の知識を覚える必要もあるね
yの増加量を求めるときどうすればいいですか?
>yの増加量を求めるときどうすればいいですか?
yの変化後の値からyの変化前の値を引けばいいよ。
詳しくは「x・yの増加量の求め方」を読んでみてね
底辺が5㎝の三角形の高さを決めると、面積が決まる…
という問題があるんですけど、この問題、「〜は・・・の関数である」という言い方で表さないといけないんです。
解き方を教えてください!
>底辺が5㎝の三角形の高さを決めると、面積が決まる…
という問題があるんですけど、この問題、「〜は・・・の関数である」という言い方で表さないといけないんです。
自分で意図的に変化させる方が「・・・」、その結果、変わってしまう方を「〜」にしよう!
とても役に立ちました!
授業中とか寝てたりらくがきしてたりしてて
全く分からなかったので
ありがたいです!!
ありがとう!頑張ろうぜ!!
変域のやりかたがいまいちよく分からないんですけど、それも教えられますかっ!?
>変域のやりかたがいまいちよく分からないんですけど、それも教えられますかっ!?
一次関数の変域の問題の解き方を読んでみて!
僕の学校の先生になってくださいっっ!www
定義域って何ですか
ありがとう!笑
>定義域って何ですか
xの変域のことかな。yの変域のことを値域ともいうね
テスト期間に入ってて、
急いで勉強しないといけなくて
分からない数学の単語がたくさん出てきたんですけど
関数の意味がいまいち分からなかったので教えていただけて本当に良かったです!
これからも、頑張っていこうと思います!
ありがとう!!頑張ろうぜ!!
関数は原点を通らなくても関数なんですか??
>関数は原点を通らなくても関数なんですか??
そうだね!
中学二年生で習う一次関数なんかは原点を通らないね!
反比例の式で、「次のx、yの関係について、yがxに反比例するものには〇を、そうでないものには✖を書きなさい。」
①面積が20平方センチメートルの平行四辺形の底辺xcmと高さycm(答えは〇)
なぜ答えが〇になるのかがどうしてもわかりません。わかりやすく説明してほしいです!
>反比例の式で、「次のx、yの関係について、yがxに反比例するものには〇を、そうでないものには✖を書きなさい。」
①面積が20平方センチメートルの平行四辺形の底辺xcmと高さycm(答えは〇)
なぜ答えが〇になるのかがどうしてもわかりません。わかりやすく説明してほしいです!
比例、反比例の利用の問題はいったん、とりあえず何も考えずにxとyの関係を等式にしてみればいいよ。
この例でいうと、
平行四辺形の面積=高さx底辺
だから、
20 = xy
になるね。
で、あとはこの等式をyについて変形してみればいいんだ。その時にその式が比例なのか反比例なのかそれともどっちでもないのかを判断すればいいよ。
詳しくは「比例と反比例の利用の解き方」を読んでみて
質問なのですがそもそも比例定数ってなんですか?私は数学はからっきし駄目で…関数も意味不明過ぎて…でも少しだけ紐どけた気がします!
学生時代、全く数学が分からなかった私。
Ken 先生の例えは目から鱗です…
もう一度勉強し直そうかな(笑)
タクシー会社の走行距離と料金
A社
・走行距離が1,500mまでは700円
・1,500mを超えると200円加算
・ 2,000mを超えるとさらに200円加算
・ 以後500mを超えるごとに200円ずつ加算
A社においてyはxの関数と言えるか言えないか
>質問なのですがそもそも比例定数ってなんですか?私は数学はからっきし駄目で…関数も意味不明過ぎて…でも少しだけ紐どけた気がします!
xとyが比例の関係にある関数において、xがいくら変化しようが定数のまま(変化しない)数字のことだ!
まずは比例の比例定数の求め方からマスターしようぜ
A君のBMI値は常に一定である.
A君の身長をx,体重をyとする時,
変数x,y,は互いに関数か.
ありがとうございます!
一緒に勉強しましょう!
>タクシー会社の走行距離と料金
A社
・走行距離が1,500mまでは700円
・1,500mを超えると200円加算
・ 2,000mを超えるとさらに200円加算
・ 以後500mを超えるごとに200円ずつ加算
A社においてyはxの関数と言えるか言えないか
yが料金、xが移動距離とすると、
xが変化するとyが料金が変化するようになってるね。ということは・・・・?
>A君のBMI値は常に一定である.
A君の身長をx,体重をyとする時,
変数x,y,は互いに関数か.
身長が変化すると、BMIを一定にするためにyも変化するから関数だ!
(500gの砂糖からxg使ったときの残りの量はyである。)
これはどうして関数なんですか?
>(500gの砂糖からxg使ったときの残りの量はyである。)
これはどうして関数なんですか?
砂糖を使った量xgによって、残りのygが変化するからね
私立なので、進みが早いです。
座標で、y=3ぶん2、x=4なのど、分数が出てきます。
こんがらがってしまって、どうすればいいのか、分かりません。
教えてください。来週テストなので、なるべく早く教えて貰うと、助かります。
解答、よろしくお願いします。
ちなみに、教科書、ニューマイスター使っています。
青色の教科書です。
>私立なので、進みが早いです。
座標で、y=3ぶん2、x=4なのど、分数が出てきます。
こんがらがってしまって、どうすればいいのか、分かりません。
分数が出て来てもやることは一緒。この問題だと、y=3ぶん2xにx=4を代入してyを求めればいいんじゃないかな。
分数の計算が不安だったら復習しておこうぜ
40人のクラスの出席者がx人で、欠席者はy人
の場合
y=40-x
てあっていますか?
この式の場合でも関数ですか?
そうだね!xが変化することでyが変化するから関数だ!
○○をただ1つに決めると、△△もただ1つに決まる。
の例文を教えて下さい。
質問じゃないんですけど、あと二日で期末テストなのに、
ワークのこれは関数だと言えますか?と、聞かれる問題のときに関数って?って、ピンとこなくてしらべてみたら、分かりやすく教えてくれて、理解でしました!!ありがとうございます!
よかった!!
反比例にも関数はありますか?
反比例は関数の一種だね!
問題で質問します。次のア〜ウの中でyがxの関数であるものを全て選びなさい。
ア1辺がx㎝の正方形の面積はy㎠である。
イ周の長さがx㎝の長方形の面積はy㎠である。
ウ1本50円の鉛筆をx本買うと代金がy円である。
非常に簡単だと思いますがこういうのがとても苦手で全く理解ができません…関数がどれか分かりやすく教えてくれませんか??お願いします
確かにこの手の問題は難しいね。
xを変化させたとき、yも変化するのが関数だと考えるとわかりやすいな
この場合だと全部関数なんじゃないかな笑
先生になってくださいぃぃぃ
kenさん多分かいりんさんの質問の答えあ、うだと思いますよ
、い、周りの長さが等しくても幅入っていとは限らないんじゃないかと思います。
間違ってたらすんまそ
確かに!長方形だもんなあ
関数と比例ってどう違うんでしょうか?
比例は関数の一種。
関数が犬だとしたら比例はチワワってところかな
最後の例題で急激に意味が分からんかった
関数分かりやすく説明してほしい。
すいません。数学関係ないですけど、浸透圧について教えてください。
実験で、濃度1%の砂糖水と水道水で豆苗と切花を育てて比較したのですが、砂糖水の濃度は同じなのに、豆苗は枯れて、切花は元気でした。どちらも浸透圧を利用して水分吸収してるはずなのに、なんでこんなに違うのでしょうか。
数1です。一次関数や二次関数を考えるときって、「YがXの関数である」式だけを関数の対象にして考えるという暗黙の了解があるのですか?「XはYの関数である」場合は関数と呼ばないののですか?
例えば、「関数y=3 x」といった式は、「関数」としか書いていなくても、「yは xの関数である」、ということで解釈すればいいのでしょうか?
教えていただけると嬉しいです。
自動販売機のお金と飲み物の関係は、金額によって飲み物がただ1つに決まらないので関数ではありません。
また、変域の説明でもお金の例を使われていましたが、xの値が0〜100まで連続していないので間違っていますよ。
めちゃくちゃわかり易かったです!
ありがとうございます( ´ω`)
つまり関数を求めるときはx×2にするということでしょうか?
(小学生なのでよくわからないだけかもしれませんwww)
関数ってあの真ん中のやつですか?
矢印と矢印の間の
既に指摘されている方がいらっしゃいますが、関数の説明としては不十分です。
xに入れる数が変化するとyに入れる数も変わるという趣旨の説明をされていますが、中2で学習する一次関数では(x,y)平面においてy=2のような定数関数が出てきます。これも「yはxの関数である」の例です。「yはxの関数である」の定義で最も重要な要素は、yの値の決まり方が一意的であるということです。
関数大変ダネー
数学って難しいよねー!
どうもあらぽんです
いつから関数ができたんですか
若干話違いますが、座標の図が何回見てもよくわかりません。
教えて下さい。
関数がわかりません
どうしたらいいですか?
とてもわかりやすかったです!!!!!
これから定期テストなので助かりました!!!!!
関数とは簡単に言えば数字を打ち込めば変換されるマシーンみたいなものなのですね
数学は得意なのですが関数だけが未だにわからなかったのでありがたいです
関数の問題で『平行四辺形の底辺が決まると、面積はただ一つ決まりますか?』という問題があり、まだこの問題はわかるんですけど、この後の『面積は底辺の関数であると言えますか?』という問題が出てきてわからないんですけど良ければ説明してくれると嬉しいです。説明下手ですみません。よろしくお願いします
平行四辺形の面積の求め方を復習しよう。
底辺だけじゃなくて高さもかけてるはず!
めちゃくちゃ分かりました
神
kennさん有難うございました!