【中2数学】図形の証明問題を攻略できる7つのコツ

図形の証明問題のコツを知りたい！

こんにちは！この記事をかいているKenだよ。コーン、最高。

図形の証明問題

ってむずかしいよね。

図形の面積を計算する問題とは

ちょっと違うタイプ。

苦手な中学生も多いはずだ。

今日はそんな苦手をなくすために、

【中2数学】図形の証明問題を攻略できる6つのコツ

っていう記事をかいてみたよ。

証明問題のせいで数学が嫌いになりそう、

ってときに参考にしてみてね笑

数学の証明問題を攻略するための6つのコツ

つぎの例題をときながら解説するよ。

AB = DC、AB // DCの△ABCと△CDAがあったとします。

このとき、角ABC = 角CDAであることを証明しなさい。

コツ1. 「仮定」と「結論」をみつける！

数学の証明問題でいちばん最初にやることは、

仮定と結論をみつけてやることさ。

仮定とは、カンタンにいってしまえば、

問題文であたえられている条件

で、

結論とは、

仮定をつかえば正しいといえること

さ。

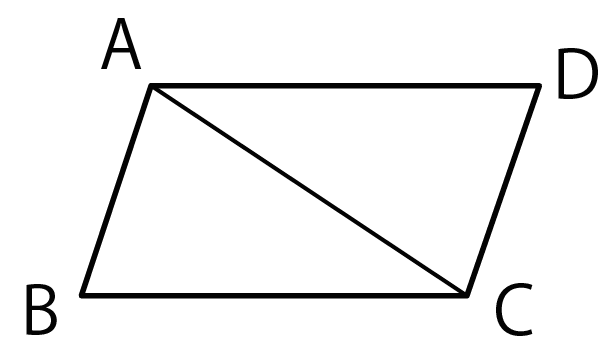
たとえば、さっきの例題でいうと、

• AB = DC
• AB//DC

っていうのが仮定だよ。

だって問題文中に、

AB = DC、AB // DCの△ABCと△CDAがあったとします。

ってかいてあるからね。

この問題にかぎっての正しい

って言ってくれてるてることなんだ。

これが仮定だ。

それじゃあ、「結論」をさがしてみよう。

結論は問題文でいうところの、

○○を証明しなさい。

の○○にあたるところさ。

つまり、

問題で証明してほしいことが「結論」なのさ。

この例題でいうと、

角ABC = 角CDA

が結論だね。

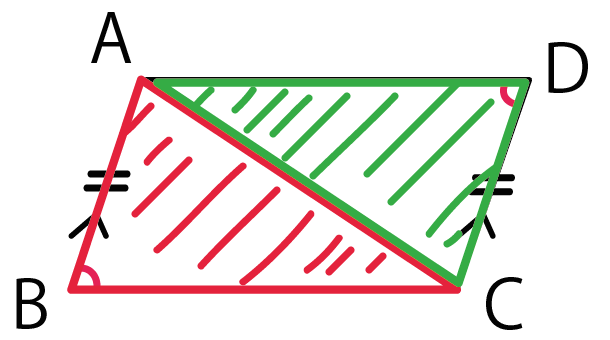
コツ2. 仮定を図に書き込んでやる！

「仮定」を図に書きこんでみよう！

これをすると、

• 証明問題を把握しやすくなる
• 結論までをイメージしやすくなる

っていうメリットがあるよ。

あと、わからなかったときでも、

テスト用紙にがんばった形跡が残って、

先生に「がんばったアピール」ができるね笑

たとえば、さっきの例題で、

• AB = DC
• AB//DC

が仮定だったよね？？

こいつを図に書き込んでやると、

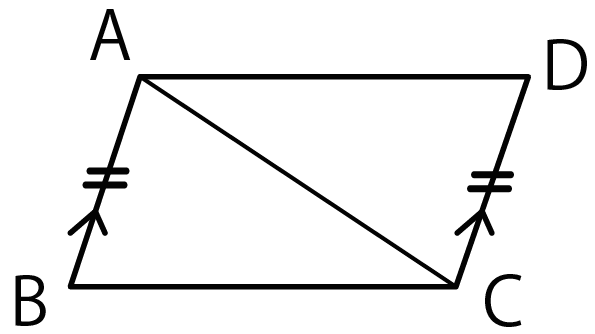
こうなる。

※図形の記号を復習してみて^^

ただ、「結論」をいっしょに書き込まないでね。

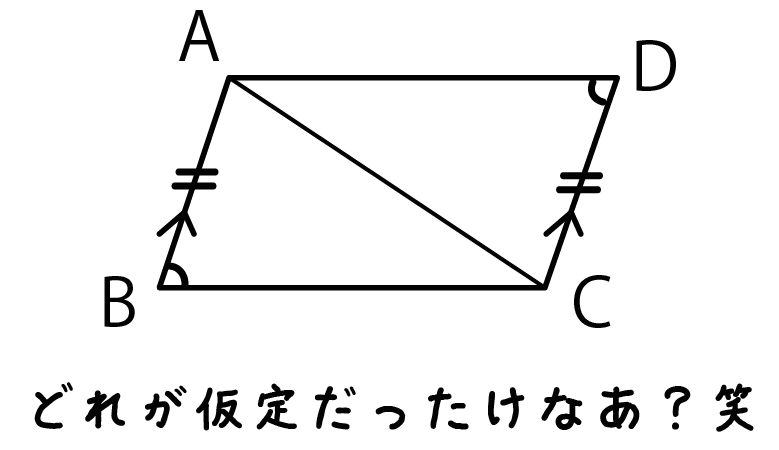
「仮定」と「結論」をごちゃまぜにすると混乱するからさ。。

結論も書き込みたいってときは、

色違いのペンでかきこんであげよう。

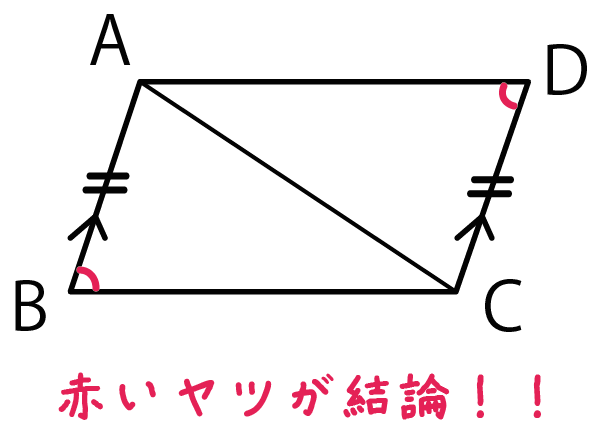
赤ペンとかでね^^

コツ3. 結論から逆算して証明をイメージする

仮定と結論を整理し終わったら、

結論までの道のりをイメージしよう。

証明問題の特徴は、

ゴールが事前にあたえられているってこと。

つまり、逆にいってしまえば、

ゴールがみえているから、そこへの行き方を考えるだけ

ってことになる。

いわば、ゴールがみえている迷路みたいなもんさ。

チーズがあるのはわかってるから、

あとは道順を考えるだけでいいんだ。

たとえば、例題の結論である、

角ABC = 角CDA

をゲットする道順を考えてみよう。

うーん、

えっと、

そうだなあ。。。

あっ！

△ABCと△CDAが合同である

ってことをいえればゴールできそうじゃね？？

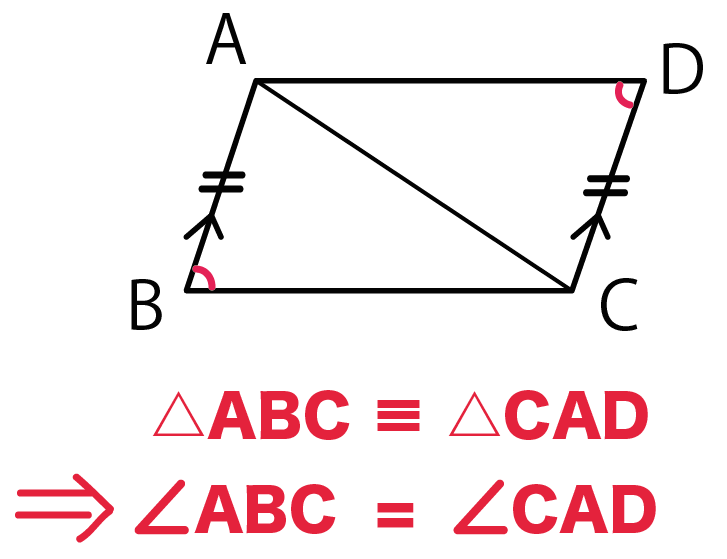
だって、

合同な図形の「対応する角はそれぞれ等しい」

ってことを使えば、

角ABC = 角CDA

がいえそうだからね。

コツ4. 根拠となることがらをたくさん覚える！

結論までをイメージするためには、

「根拠となることがら」を覚えている必要があるんだ。

多ければ多いほどいいね。

たとえば、さっきの例題でも、

合同な図形の性質

を暗記していないとゴールまでイメージできなかった。

「合同な図形の性質」以外にもたとえば、

• 三角形の合同条件
• 平行線の性質
• 平行四辺形になる条件
• 直角三角形の合同条件
• 二等辺三角形の性質

・・・・・・・・

などなど、図形の性質や合同条件をおぼえていればいるほど、

証明問題はときやすくなる。

辛いけど、これが事実だ。

最初はおぼえられなくても大丈夫。

徐々に問題をときながらみにつけていこう！

コツ5. 対応順にアルファベットをかく

アルファベットといえば、

A, B, C, D , E, F, G……

という順番だね。思わず歌いだすやつもいるかもしれない。

ただ、証明問題においては、

アルファベット順に英文字を並べるのはNG

なんだ。

たとえば、例題で、

赤と緑の2つの三角形について証明していくよ

っていいたいとしよう。

このとき、なにも考えずにアルファベット順に、

△ABCと△ACDにおいて

とか書いちゃダメだ。

なぜなら、

対応する頂点同士の順番になっていないから

だ。

こういうときは対応する頂点の順番で、

△ABCと△CDAにおいて

ってかいてあげよう。

先生によっては対応する順番でかかないと×ってひともいるから

きをつけてね^^

コツ6. とりあえず番号をふっておこう！

証明問題でみちびいたことに「番号」をふろう！

たとえば、

AB = DC (仮定)・・・・・・（1）

といった感じで。

なぜ大事なのかというと、

結論をみちびく材料として使いやすくなるから

なんだ。

ただ単に、

以上のことより、△ABC ≡ △DACである

っていうよりも、

(1)、(2)、(3)より、△ABC ≡ △DACである

っていったほうが説得力があるからね。

番号をつけるのはタダ。無料さ。

番号のつけすぎで減点されないから大丈夫。

引用しやすいようにこまめに番号をつけよう！

コツ7. 担当の先生の書き方をマネする

証明問題の書き方にはたーくさんある。

先生によって書き方がちがう。

たぶん、誰を信じたらいいかわからなくなるはずさ笑

そんな状況だからこそ、

先生流の書き方で証明問題をかいてあげよう！

ぼくが中学生のときも困惑したよ。

先生によっては、三角形の合同条件を、

• 三辺相等
• 二辺夾角相等
• 二角夾辺相等

ってかかないと×にするヒトもいたし。

だから、

担当の先生の書き方で証明をかいてあげること

が高得点をとる秘訣になってくる。

数学の先生の板書をしっかりとって、

テスト前に書き方をおぼえてみよう！

いや、ぜんぜん書き方がわからない！

ってときは、

証明問題の書き方の記事を参考にしてみて^^

まとめ：数学の証明問題は7つのコツでどうにかなる！笑

数学の証明問題はぶっちゃけむずい。

だけど、この記事で紹介した7つのコツで、

1. 仮定と結論をみつける
2. 仮定を図にかきこむ
3. 結論から逆算してイメージ
4. 根拠となることがらを覚える
5. アルファベット順はやめる
6. とりあえず番号をふりまくる
7. 担当教師の書き方をマネる

ちょっとだけラクになるはず。

やっかいな単元だけどがんばっていこう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。