3分でわかる！二等辺三角形の2つの定理・性質

二等辺三角形の性質・定理ってなに？？

こんにちは！この記事をかいているKenだよ。馬、うまいね。

二等辺三角形って、

2つの辺が等しい三角形のこと

だったよね？？

名前はかっこいいし、

ルックルも、いい。

人気がありそうな三角形だ。

だけれども、

二等辺三角形にはどんな性質があるんだろう？？

って疑問に思うよね。

そこで今日は「二等辺三角形の性質・定理」をわかりやすく説明していくよ。

よかったら参考にしてみて^^

二等辺三角形の2つの性質・定理

二等辺三角形には2つの性質があるんだ。

1. 2つの底角は等しい
2. 頂角の二等分線は、底辺を垂直に2等分する

ってやつだ。

順番にみていこう！

性質1. 「2つの底角は等しい」

ひとつ目の性質は、

底角が等しい

ってやつさ。

底角とは、

底辺をはさんでいる角のこと

だったね？

なんと、

二等辺三角形では底角の大きさが等しいんだ。

たとえば、つぎの二等辺三角形ABCがあったとしよう。

• AB = AC
• 角B＝50°

っていうスペックをもっているヤツさ。

このとき、

二等辺三角形の底角は等しいから、

角B = 角C = 50°になるんだ。

頂角はどうなるかっていうと、

内角の和180°から2つの底角をひいて、

180°- (50+50)
= 80°

で計算できるよ。

性質2. 「頂角の二等分線は底辺の垂直二等分線」

2つの目の性質は、

「頂角の2等分線」が「底辺の垂直2等分線」になる

ってやつだ。

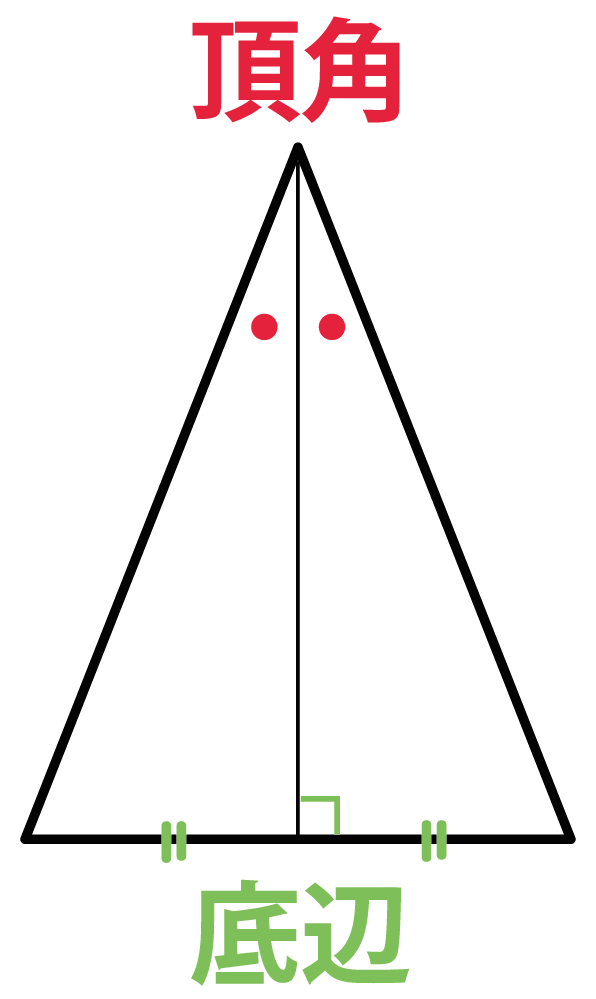
びみょうにすごいよね？笑

たとえば、つぎの三角形DEFがいたとしよう。

• 頂角D = 70°
• 底辺EF = 6 cm

っていうスペックをもっている。

このとき、

頂角Dの二等分線を底辺EFにむけてひいて、

底辺との交点をGとする。

すると、

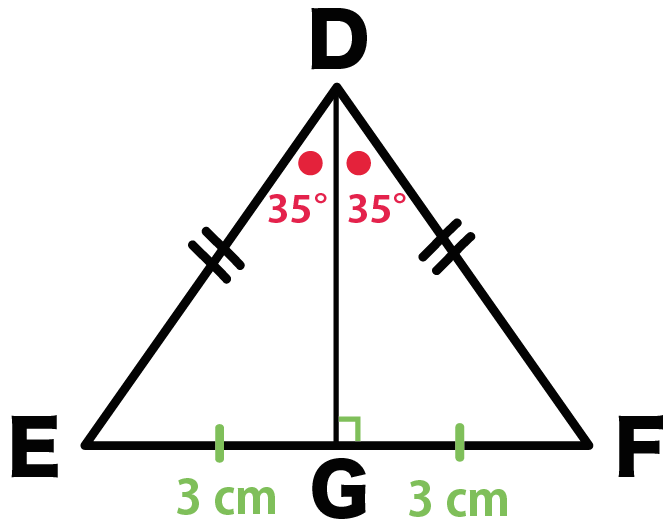
• EG = FG = 3 cm
• 角EGD = 角FGD = 90°

になるよ。

つまり、

DGは底辺EFの垂直二等分線になっていると

いうことなんだ。

まとめ：二等辺三角形の底角と二等分線を使いこなせ！

二等辺三角形の性質の、

• 底角が等しい
• 頂角の二等分線は底辺の垂直二等分線である

ってことを解説してきたよ。

この性質は定理として、

証明や計算問題で自由につかうことができる

んだ。

じゃんじゃんつかって問題を攻略していこう！

そんじゃねー

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。