正四角錐の体積の求め方の公式って??
こんにちは!この記事をかいているKenだよ。青い空が好きだね。
正四角錐の体積の求め方には公式があるんだ。
正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。
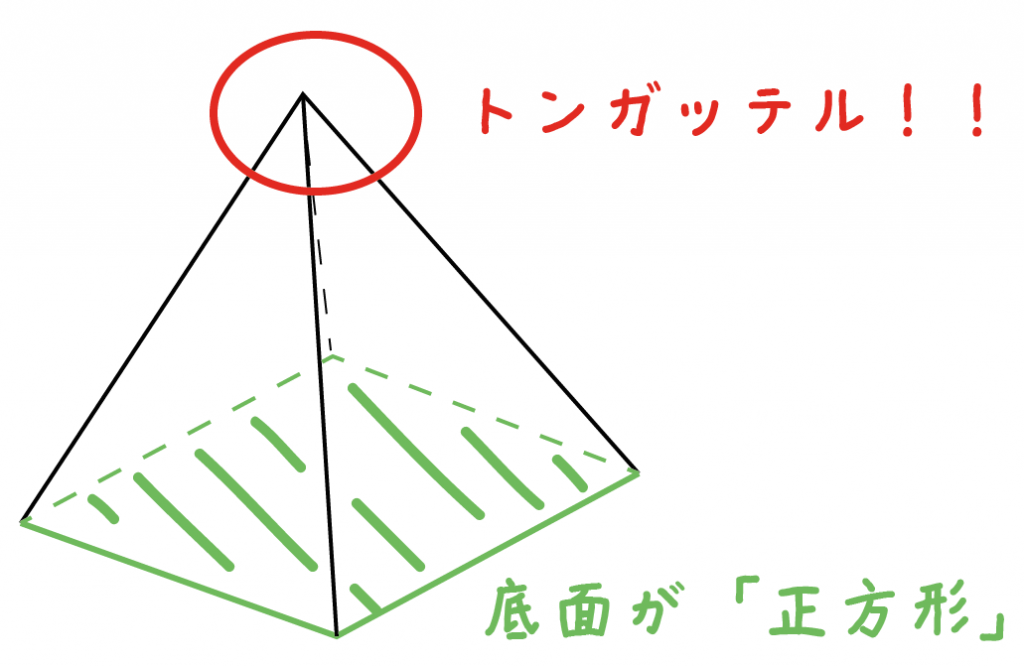
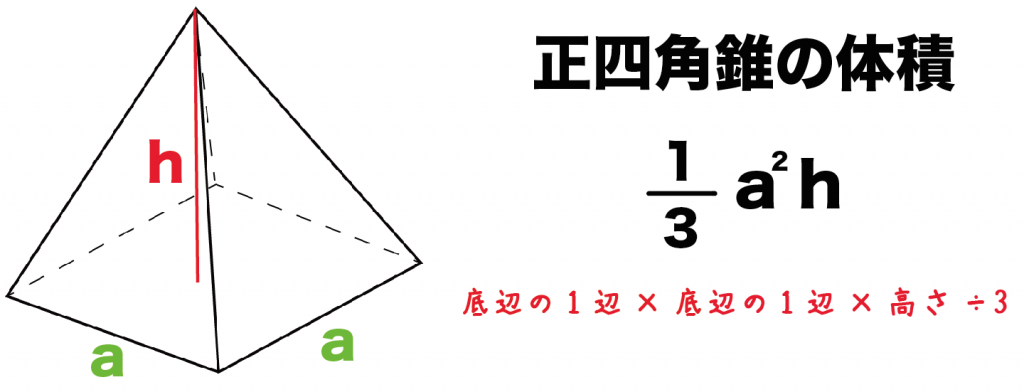
底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。
1/3 a²h
つまり、
(底辺の1辺)×(底辺の1辺)×(正四角錐の高さ)÷3
ってことだね。
今日は、この計算公式をどうやって使うのか??
ということをわかりやすく解説していくよ。
正四角錐の体積の求め方がわかる3つのステップ
正四角錐の体積は3つのステップで計算できちゃうんだ。
例題をときながらみていこう!
底辺の1辺の長さが6 [cm]、高さが8 [cm]の正四角錐の体積を求めてください。

Step1. 底面積を計算するっ!
まずは正四角錐の底面積を求めてみよう。
正四角錐の底面は「正方形」だよね?? 正方形の面積を「1辺×1辺」という公式をつかって計算してくれ。

例題でいうと、
底面の正方形の1辺は6[cm]だよね。だから、底面積は、
6×6 = 36[cm²]
になる。
Step2. 正四角錐の高さをかけるっ!
さっき計算した底面積に「高さ」をかけてみよう!
例題の正四角錐の高さは8 [cm]だから、
36×8
= 288[cm³]
になるね。

計算ミスに気をつけてね^^
Step3. 最後に1/3をかける
底面積に高さもかけたし・・・
と安心してはダメ。
先がとんがっているタイプの「錐体」では、体積を求めるときに必ず「1/3」をかけなきゃいけないんだ。
えっ。なぜ1/3をかけるのかって??
それは円錐の体積の求め方でも触れたけど、
高校数学でならう「積分」を使わないと説明できないんだ。
だから、中学数学ではとりあえず、
先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる
って覚えておけば問題ないよ。
だから例題の正四角錐の体積は、
6×6×8×1/3
= 96[cm³]
になるんだ。

おめでとう!これで正四角錐の体積を計算できたね^^
まとめ:正四角錐の体積の求め方も大丈夫!
正四角錐の体積の公式はどうだった??
底面積×高さ×1/3
という計算をゆっくりしてみてね。テスト前に復習しておくと心強いかも!
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。
























表面積の計算の仕方を教えてください、
まずは展開図書いてみよう!
表面積はこの記事を参考にしてね〜
その高さが分かってない時どうやって求めるんですか?
>その高さが分かってない時どうやって求めるんですか?
高さを三平方の定理で計算してみよう。
詳しくは「正四角錐の高さの求め方」を読んでみて
4×4×7÷3/1は、どうすれば良いですか
>4×4×7÷3/1
分数の割り算の時は、÷の後ろの分数の分母と分子をひっくりかえすといいよ
高さが3√7の場合はどうやって計算すればいいですか?
>高さが3√7の場合はどうやって計算すればいいですか?
底面積÷3x高さで計算しよう
底辺の1辺が8cmの正方形で、AB=9cmの正四角錐の高さってどうやって求めればいいですか?
>底辺の1辺が8cmの正方形で、AB=9cmの正四角錐の高さってどうやって求めればいいですか?
正四角錐の断面図で三平方の定理を使ってやるよ。
詳しくは正四角錐の高さの求め方を読んでみて
高さが2√5のときはどう計算したらいいですか
>高さが2√5のときはどう計算したらいいですか
高さがルートでも計算方法は同じだよ!
6×6×√7×三分の一はどうすればいいですか?
>6×6×√7×三分の一
まずはルート以外の掛け算を計算して分数を約分して綺麗にしよう。
最後にルートの計算だね
AB=AC=AD=AEで、表面BCDEが正方形の正四角錐である。またFは辺AC上 の点でBFで、AF合同ACである。AB=8cm.FC=1cm
この正四角錐の体積は何cm3か
>AB=AC=AD=AEで、表面BCDEが正方形の正四角錐である。またFは辺AC上 の点でBFで、AF合同ACである。AB=8cm.FC=1cm
この正四角錐の体積は何cm3か
「AF合同AC」のところがちょっとわからない!三角形とか図形のはずだ!
底面積を求めるための1辺がはっきりしていない場合どうすればいいですか?
>底面積を求めるための1辺がはっきりしていない場合どうすればいいですか?
どんな手を使ってもいいから底面積を求めてみよう!
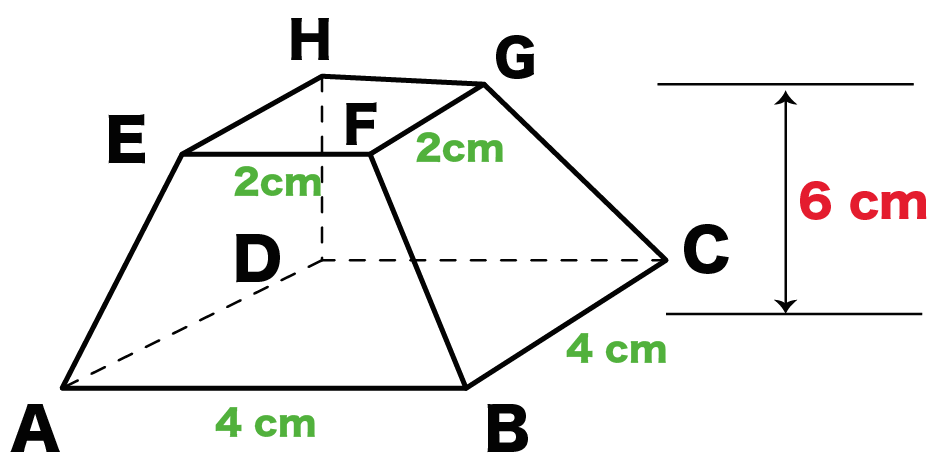
一辺の長さが4㎝ 高さが6㎝の表面積の求め方はどうすればいいですか?
円錐の体積の求め方を教えてください。
>一辺の長さが4㎝ 高さが6㎝の表面積の求め方はどうすればいいですか?
まず展開図をかいてみるといいよ!
そしたら底面の正方形、側面の三角形たちの面積を順番に計算して足してみよう
>円錐の体積の求め方を教えてください。
円錐の体積の求め方を読んでみて!
中学受験新演習小6実力アップ問題集の、第19回[立体の切断]の標準演習の5番の(1)は、どうやって解くのか。
問題送ってみて!
いつも見させて頂いています!
ありがとうございます!
ありがとう!!
角度があるときはどーすればいんですか?
何倍かを問われたらどうすれば?