【徹底解説】マイナスかけるマイナスはなぜプラスか？？

マイナスかけるマイナスはなぜプラスになるのかな？？

中学数学を勉強し始めて最初にぶつかる壁があります。それは、

マイナスかけるマイナスはなぜプラスになるのか？？

ということです。ゼロより小さいマイナスの数をかけたら、なぜ計算の答えがもとの数より大きくなってしまうのか？？　不思議すぎます。

こんなことが許されるなら、借金（マイナスのお金）に借金をかけ合わせればプラス、つまりお小遣いになりそうです笑

そんなのゼッタイおかしいですよね？？

そこで今日は「マイナスかけるマイナスがなぜプラスになるのか？？」という全国の中学生の疑問に答えるために解説してみました。

答えが気になって夜も眠れない中学生の方！！ぜひ参考にしてみてくださいね。

プラスかけるプラスはプラスになる！

まずは正の数と正の数のかけ算の場合を考えてみましょう。小学校で勉強した算数の延長ですね。たとえば、

という計算式があっとしましょう。小学二年生で勉強した九九で瞬殺すると、2秒でこの答えが6であることがわかります。だって、「サンニガロク！」ですからね。

で、でもちょっと待ってください。

そもそも「掛け算」って何でしょうか？？　うまく説明できるでしょうか？？

ぼくは「掛け算」は次のような計算のことだと思っています。それは、

「ある数のセット」を「ある方向」に「掛ける数ぶん」だけ0から増やす行為

です。えっ。ぜんぜんわかりませんですって？？！　そんな方のために先ほどの「」という計算式を例にとって考えてみましょう。

この計算式では「3という数字セット」を「そのままの方向」に「2つ」増やしています。もうお分かりですよね？　赤字の文章と対照させて考えると、

「3という数字セット」=> 「ある数のセット」

「ある方向」=>「そのままの方向」

「2つ」=>「掛ける数ぶん」

となります。数直線を使って視覚的に考えてみるとこうなります。

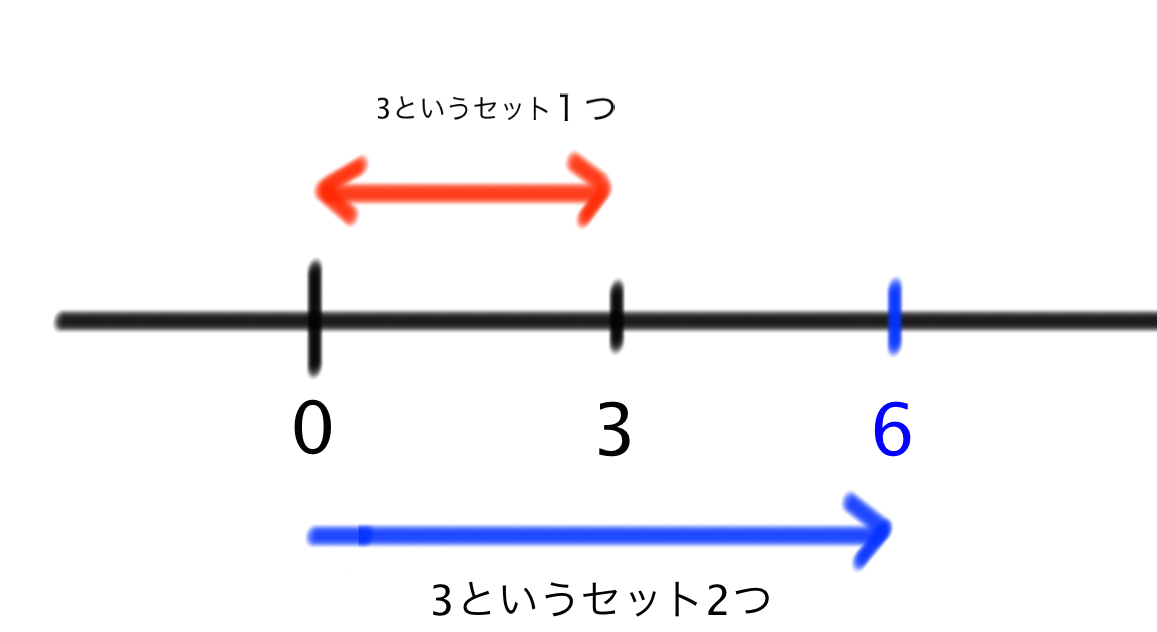
3という数のセットを正の数に2つぶん増やした数。それが答えの6になります。

これが「正の数」×「正の数」の掛け算の場合ですね。

プラスかけるマイナスはマイナス！？

つづいては正の数に負の数（マイナス）をかけた場合です。プラスとマイナスの掛け算はどういう結果になるでしょうか？？

今度はという計算式の例で考えてみましょう。

「ある数のセット」を「ある方向」に「掛ける数ぶん」だけ増やす行為

を掛け算だとすると、この計算式は、

「3という数のセット」を「逆の方向」に「2つ」増やす

と答えが算出されることになります。なぜここでは「ある方向」が「逆の方向」なのでしょうか？？

それは、

掛ける数がマイナス（負の数）だからです。

×の前の数字にマイナスがついていたら逆の方向に数のセットを増やさなければいけません。よって、この掛け算の結果は負の数の「-6」になります。

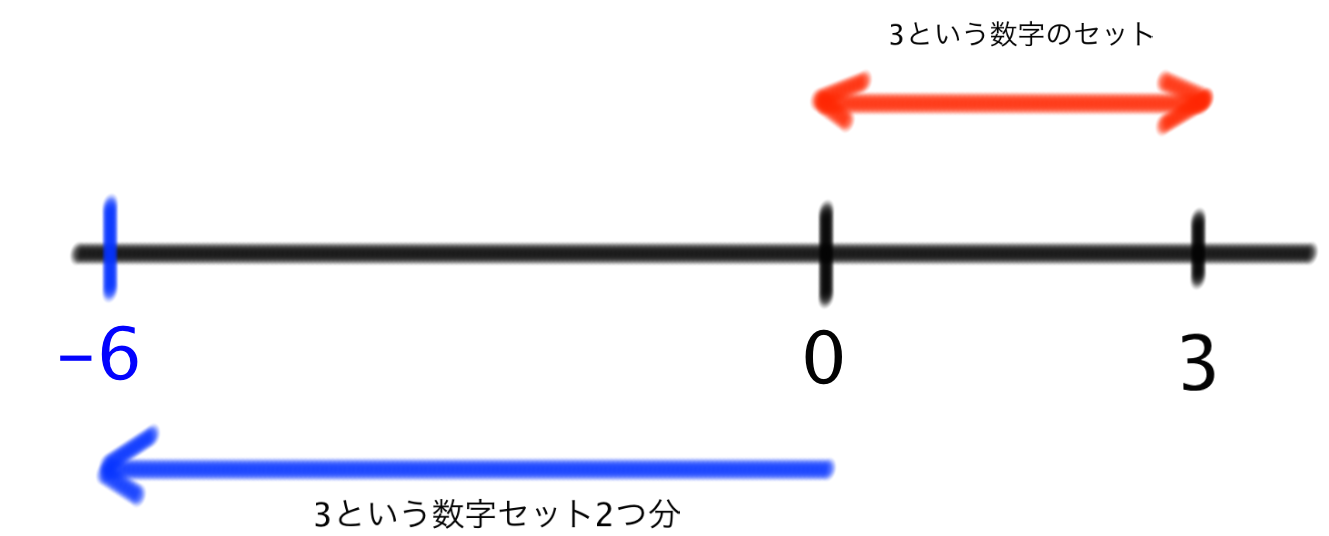
ここで大切なのは、

マイナスを掛けると逆方向に数字セットを増やさなければならない

ということです。ここをしっかり押さえておけばどんなマイナスの掛け算にも対処することができますよ。

マイナスかけるマイナスはプラス！！

さて、お待ちかねの「マイナスかけるマイナスはなぜプラスになるのか」ということを見て行きましょう。ちょっと難しく見えますが、基本は上であげた2つの例と変わりません。

「ある数のセット」を「ある方向」に「掛ける数ぶん」だけ増やす行為

が掛け算ということを押さえておけば十分です。それではマイナスの掛け算の例題を見て行きましょう。たとえば、「」という計算式をみていきます。

これは-3というマイナスの数に-2というマイナスの数を掛けています。掛ける数の符号がマイナスであること注意すると、

「-3という数字セット」を「逆の方向」に「2つ」だけ増やす

とこの計算式の答えをゲットできます。やりましたね！数直線で考えてみると、

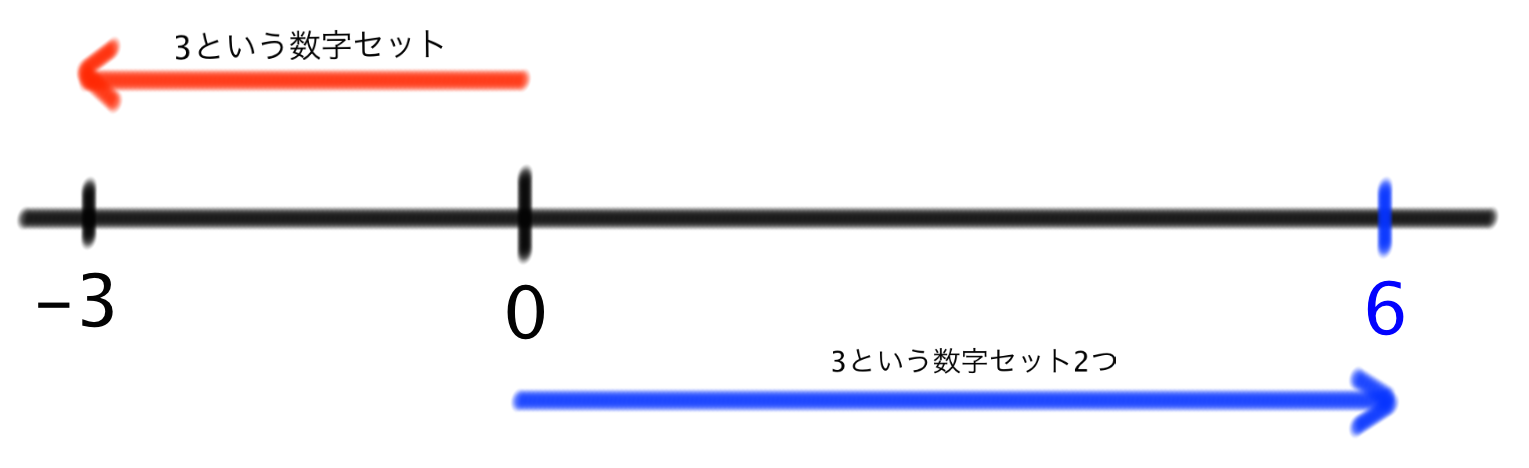
このようになります。マイナスの数字セットである(-3)を「負とは逆方向」に2つ増やします。

したがって、計算の答えはプラスの「6」ということになります。

えっ。いちいち数直線を考えるのがメンドクサイですって？！？　そういう横着な中学生の方は「マイナスとマイナスをかけるとプラスになる！」という事実を暗記しておきましょう。そうすれば一瞬でマイナス同士の掛け算を計算できますね！いやあー便利便利^^

まとめ：掛け算にふくまれる「マイナスの数」を数えろ！

ここまで「プラス×プラス」、「プラス×マイナス」、「マイナス×マイナス」という3つのパターンの掛け算をみてきました。ただ、これらすべてのパターンを暗記するだけだと計算の限界があります。

なぜなら、

項が3つ以上の掛け算（乗法）に対応できないから

です。たとえば、という計算式があったとしましょう。すると、

あれ？　マイナスかけるマイナスかけるマイナス？？？　ちょ・・・ちょっと待ってよお・・・

なんて事態になりかねません。そこで登場するのが、

乗法の計算式に含まれる「マイナスの項」を数える裏技

です。マイナスの数が「偶数」と「奇数」の2つの場合で計算結果の符号が変わるとおぼえておきましょう。

• マイナスの項の数が偶数→プラス
• マイナスの項の数が奇数→マイナス

という具合にです。たとえば、ではマイナスの項が3つありますので、計算結果の符号はマイナスになります。

また、という計算式の場合、マイナスの項の数がぜんぶで4つの偶数個あります。よって、答えはプラスになるわけですね。

えっ。この裏技が使える理由を知りたいですって？！？

そうですね。これは負の数を掛けると「逆の方向に数のセットを増やす」という掛け算の性質のためです。つまり、負の数がひとつ増えるごとに逆の方向に増やさなくてはなりません。

そうですね、電車の線路の方向を切り替えるようなイメージです。もしくは、ネッシーの首を交互にひねるような感覚です。も、もしくは、好き・嫌い・好き・嫌い・・・のような花占いのものです笑

これは中学数学を通して頻繁に出題される問題です。しっかりと頭にたたき込んでおきましょう。

それでは、また今度です。

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。