円周角の定理の逆の証明??
ある日、数学が苦手なかなちゃんは、
円周角の定理の逆の証明がかけなくて困っていました。
円周角の定理の逆を証明してみよう!
いきなり証明って言われても……
いったん分かると便利!
いろんな問題に使えるんだよな。
円周角の定理の逆って、
そんなに便利なの?
まあね。
円の性質の問題では欠かせないよ。
円周角の定理すら覚えてないのに……
そんなときのために!!
円周角の定理をサクッと復習しよう。
【円周角の定理】
1つの円で弧の長さが同じなら、円周角も等しい
∠ACB=∠APB
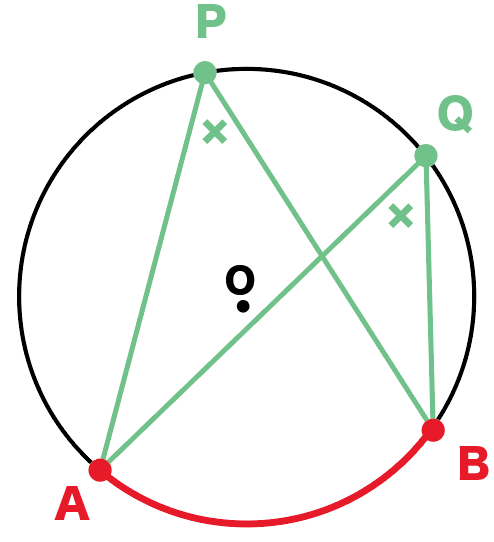
なるほど!
少し思い出せた!
【円周角の定理の逆】
2点P、 Qが線分ABを基準にして同じ側にあって、
∠APB = ∠AQB
のとき、
4点ABPQは同じ円周上にある。

ちょっとわかった気がする!
その調子で、
円周角の定理の逆の証明をしてみようか。
はい!!
3分でわかる!円周角の定理の逆とは??
さっそく、
円周角の定理の逆を証明していくよ。
どうやって?
証明するの?
つぎの3つのパターンで、
角度を比べるんだ。
- 点 Pが円の内側にある
- 点 Pが円の外側にある
- 点Pが円周上にある
つぎの円を思い浮かべてみて。
点Pが円の内側にあるとき、
∠ADBと∠APBはどっちが大きい?
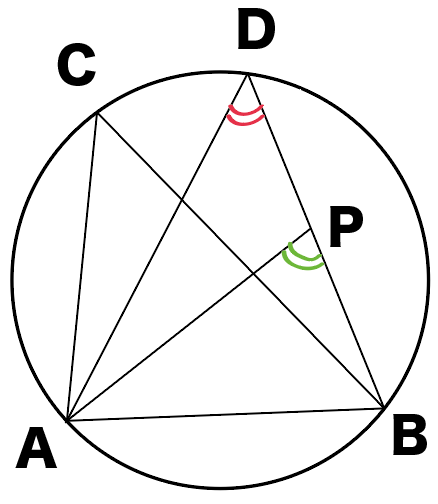
そう!
点 Pが円の外にあるときは?

∠ADBの方が大きい!
そうだね!
今わかってることを書いてみよう!
点Pは円の内側になると、
∠ADB<∠APB
になって、
点Pが円の外側になら、
∠ADB>∠APB
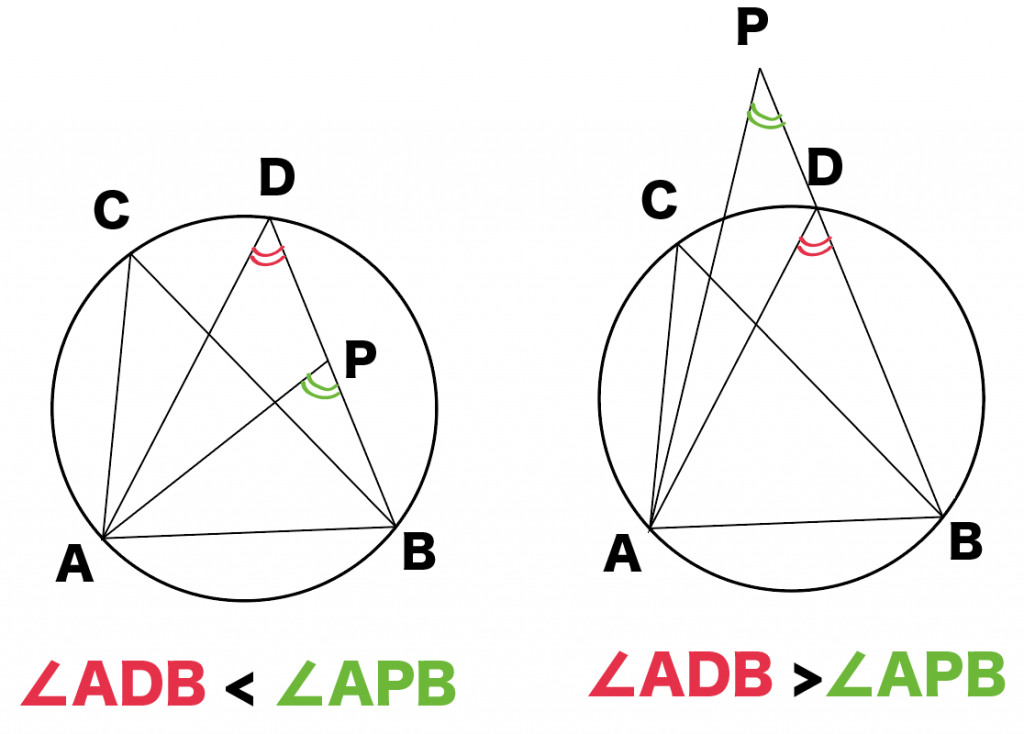
おっ、いい感じだね!
点Pが円上のとき、
∠ADB=∠APB
じゃん!
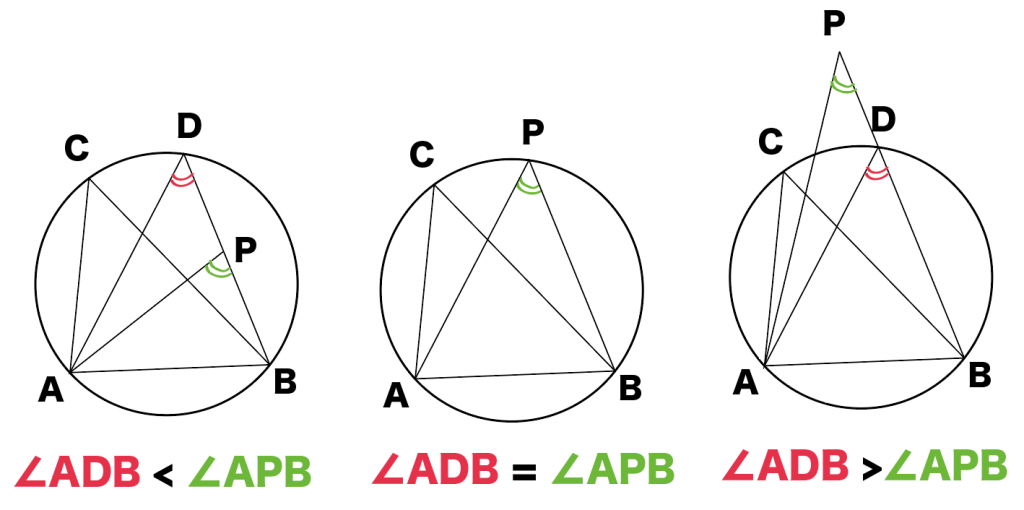
そういうこと!
点 Pが円の内側に入っちゃったり、
円の外側に出ちゃったりすると、
角度は等しくなくなっちゃうよね。
はい!
点 Pが円周上にあるときだけ、
2つの角度が等しくなるってわけ。
なるほど!
ってことは、これが証明なんだ。
そう。
円周角の定理の逆の証明はこれでok。
いつもの証明よりは楽だったかも^^
まとめ:円周角の定理の逆の証明はむずい?!
円周角の定理の逆の証明はどうだったかな?
3つの円のパターンを比較すればよかったね。
- 点 Pが円の内側にある
- 点 Pが円の外側にある
- 点Pが円周上にある
図を見れば当たり前のことだったなあ
いうねえ
やってみると分かりやすかった!!
まずはあきらめず挑戦してみて!
うす!

年齢不詳の先生。教育大学を卒業してボランティアで教えることがしばしば。


























質問ではないですが、誤植があったのでご報告します。
記事の中盤あたりで…
【円周角の定理の逆】
2点P、 Qが線分ABを基準にして同じ側にあって、
∠APQ = ∠AQB←ココ
のとき、
4点ABPQは同じ円周上にある。
∠APQ = ∠AQB→∠APB = ∠AQB です。
ご指摘ありがとうございます
点Pが円の内側にあるとき、なぜ. 三角形APBが大きいのですか?
見た目で判断するのは証明とは言わないのでは?
見た目で判断しているように見えますけど,内角と外角の関係を考えれば式でも簡単に書けるので,「証明の説明」としてはこれで十分だと思います。