筆算の平方根の求め方ってあるの??
こんにちは!この記事をかいてるKenだよ。映画がよんでるね。
この前勉強した平方根の求め方は基本的なヤツだ。
「√」をかぶせるだけだもんね。
今日は、もう少し進化した、
筆算をつかった平方根の求め方
を紹介していくよ。
よかったら参考にしてみて。
= もくじ =
- 筆算はなんのためにつかうの?
- 筆算の計算5ステップ
どんなときに筆算で平方根を求めるの??
筆算をつかった平方根の求め方を、
開平法
とよんでるよ。
中学数学では勉強しないんだけどね。
えっ。
どんなときに開平法をつかうかって!?
つぎの3つのときが多いよ。
- デカい数の平方根を求めるとき
- 小数点以下のケタ数をだしたいとき
- 小数の平方根をだすとき
今日はそのなかでも、
でかい数の平方根を求める問題
を解説しいこう。
例題をいっしょにといてみようぜ。
271441の平方根を求めなさい。

Step1. √でくくる
平方根を求めたい数を「√」でくくろう。
「√」をうえにのっければいいんだ。
例題では「271441」にルートをのせてみて。

Step2. 右端から2ケタずつ区切る
ルート内の数字を右から2ケタずつ区切ろう。
「|」で区切ってみてくれ。
例題の271441はこうなるはずだ↓↓
27|14|41

Step3. 二乗すると「左の塊」に近くなる数は?
1番左の2ケタの塊に注目してくれ。
2乗したらその塊になる数を考えればいいのさ。
例題でいうと、
- 27
- 14
- 41
の3つの塊ができてるよね??
んで、いちばん左の塊は、
27
だ。

2乗して「27」に一番近くなる自然数は、
5
だ。
なぜなら、
5の2乗 = 25
だからね。
そいつを、
- 「√」の左外のスペース
- 27のうえ
にかいてね。

Step4. 二乗した数をかく
2乗した数をかこう。
かく場所は、いちばん左の塊の下だ。
例題では5を2乗したらできる「25」を、
いちばん左の塊の「27」の下にかこう。
こうなるはずだ↓↓

Step5. 引き算する
左の塊から2乗の数をひこう。
例題でいうと、
27 – 25
ってわけだね。
こいつを計算すると、
2
になる。
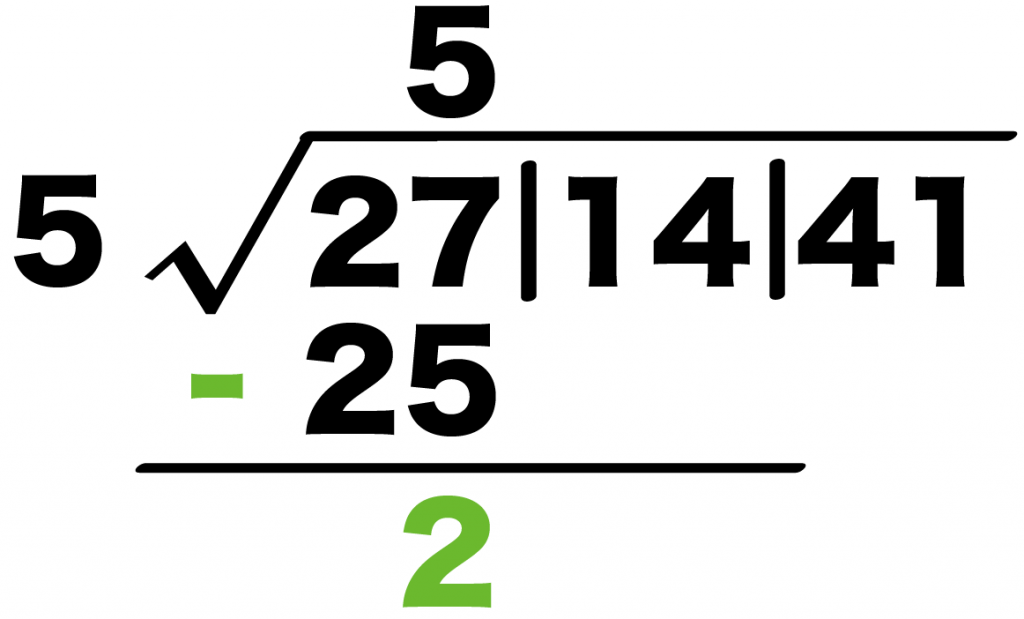
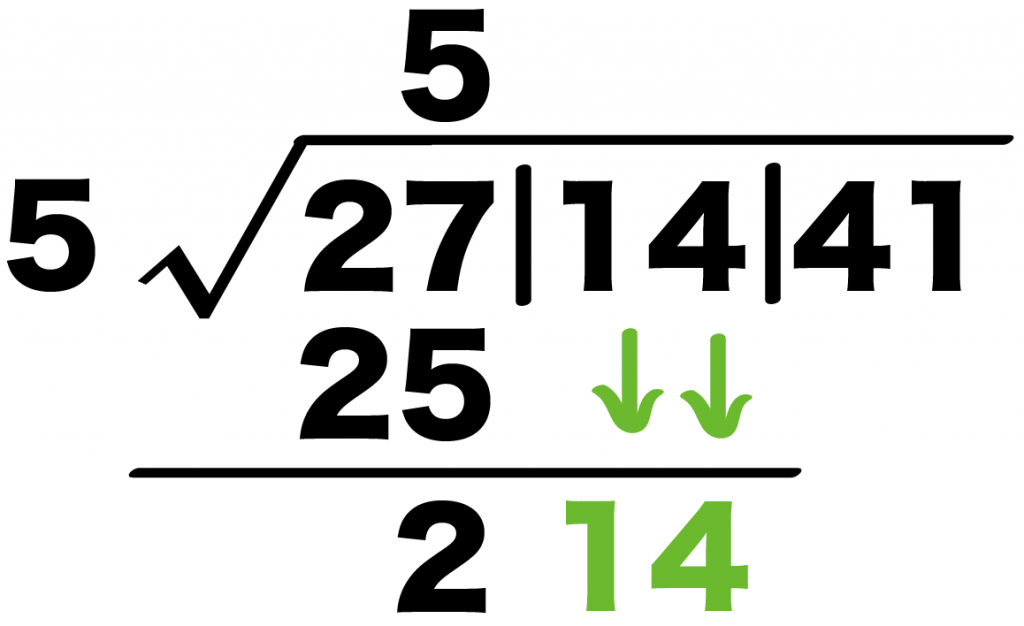
Step6. 2ケタの塊をおろす
隣の2ケタの塊を下におろそう。
例でいうと、「14」を2の右に召還するのさ。
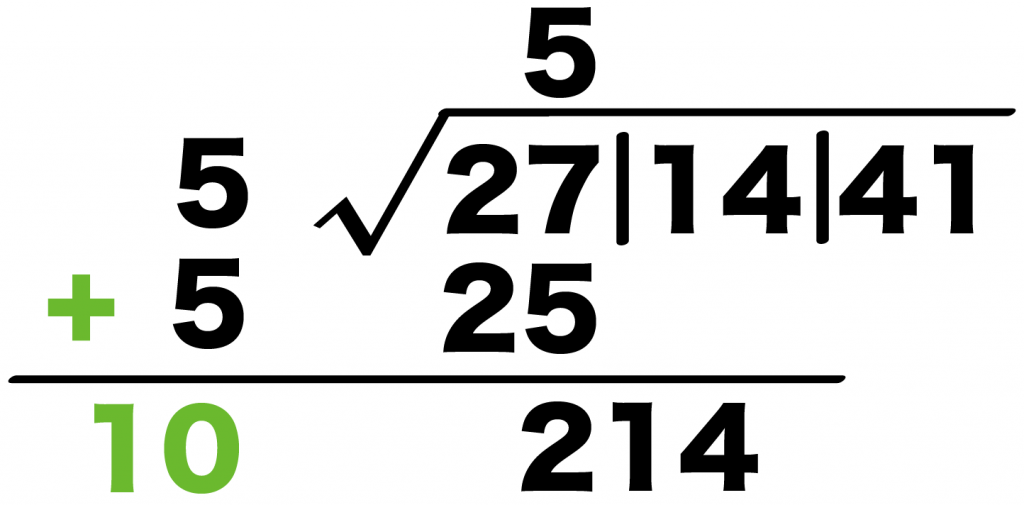
Step7. 一の位をたす
左の数の一の位を、左の数自身にたそう。
例でいうと、左の数は「5」だね。
こいつの1の位は5だから、
5+ 5
= 10
になるわけだ。
Step8. 「ある数」×「1の位をある数にした数」が引き算の結果にいちばん近いものをさがす
ちょっと言葉にしずらい・・・
ここでは、「ある数」を推測してほしいんだ。
その「ある数」とは、
「ある数」×「1の位をある数にした数」がさっきの「引き算の結果」にいちばん近いやつ
なんだ。
自分でも何いってるかわからないや笑
ちょっと例題をみて。
14のうえの「ある数」を推測するわけだ。
わかりやすくするために、ここでは、
(ある数) = □
としようか。

一の位をある数にした数っていうのは、
10□
になるってわけだ。
だからさっきいってたのは、
□ × 10□ = 214
になるような□をみつければいいってことなのさ。

□に1から順番に代入して調べてみると、
どうやら、
□に2を入れたときに204になって一番214に近くなるみたい。
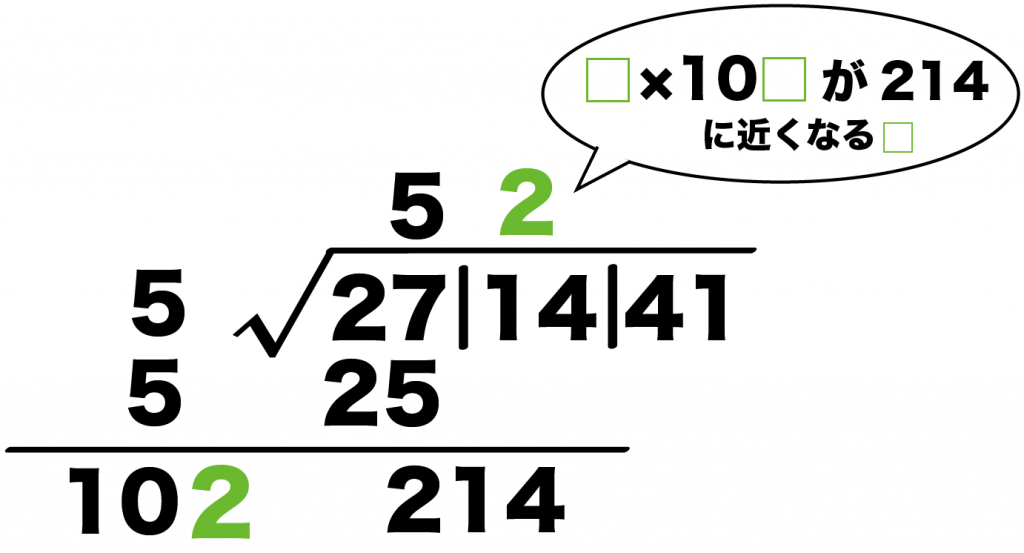
だから、ここでは□に2がはいるね。
Step9. 掛け算の結果をかく
「いちばん近くなった数」を「引き算の結果」の下にかいて。
練習問題でいうと、
214の下に204をかけばいいのさ。
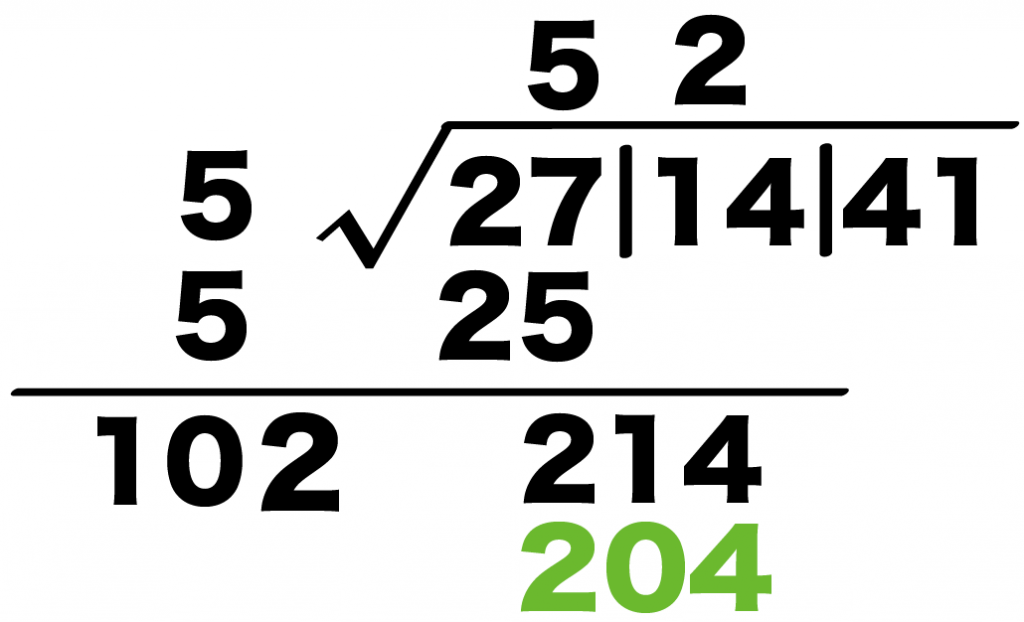
Step10. 引き算する
「引き算の結果」から「掛け算の結果」をひこう。
流れは、Step5といっしょだ。
例題でも「引き算の結果」から「掛け算の結果」をひいてやると、
214 – 204
= 10
になるね。

Step11. 「2ケタの塊」を下におろす
「引き算の結果」の右に「最後の塊」をおろそう。
例題でいうと、41を10の右におとせばいいんだ。
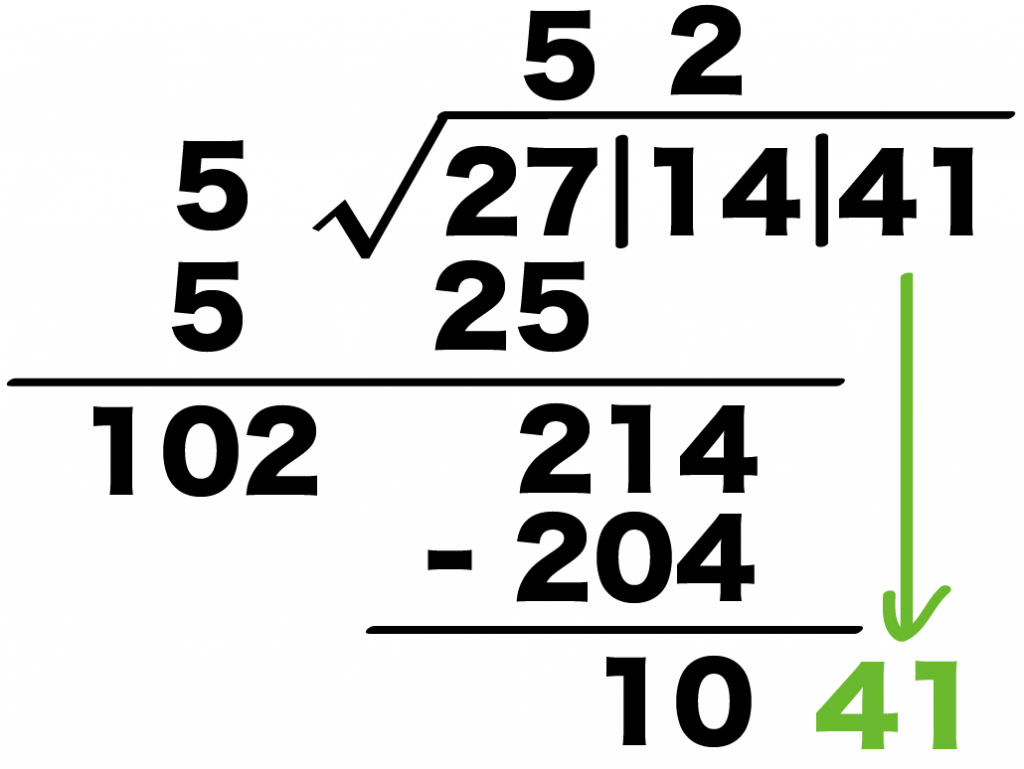
Step12. 一の位をたす
つぎは左の数に注目してくれ。
こいつの1の位を自分自身にたせばいい。
例題でいうと、左の数は102。
こいつの1の位は2だから、
102 + 2
= 104
になるね。

Step13. 「ある数」×「1の位をある数にした数」が引き算の結果にいちばん近いものをさがす
いよいよ最後のステップ。
やり方はStep8とおなじだ。
例題でいうと、
最後の塊のうえにくる数を□とする。
んで、
□ × 104□
が
1041
になるような□をゲットすればいいのさ。

□に1から順番にいれてみると・・・・
おっ。
□に1いれたら1041に等しくなるやん!?
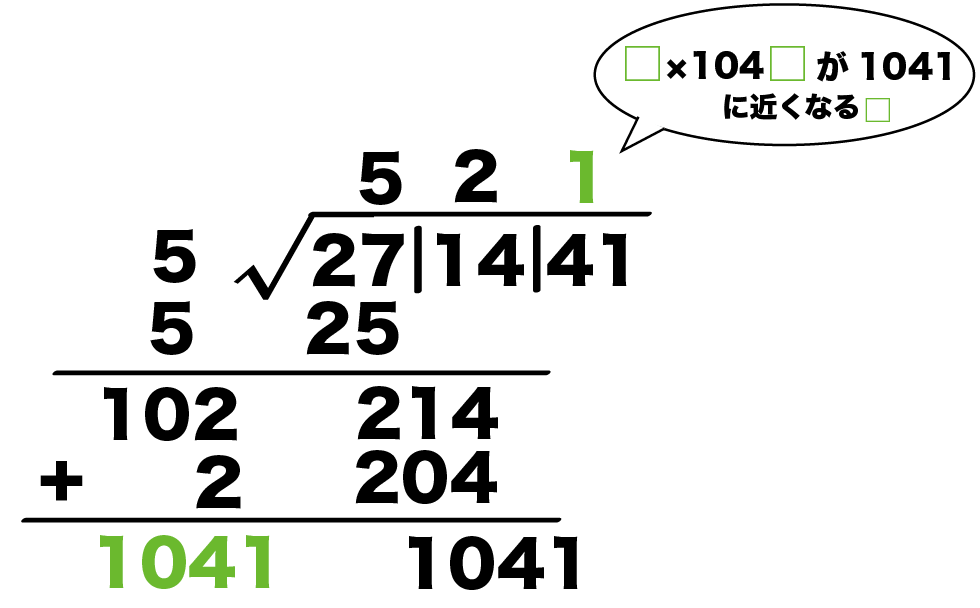
だから、さっきみたいに筆算を続けてやると、
最終的に引き算の答えが0になるね。
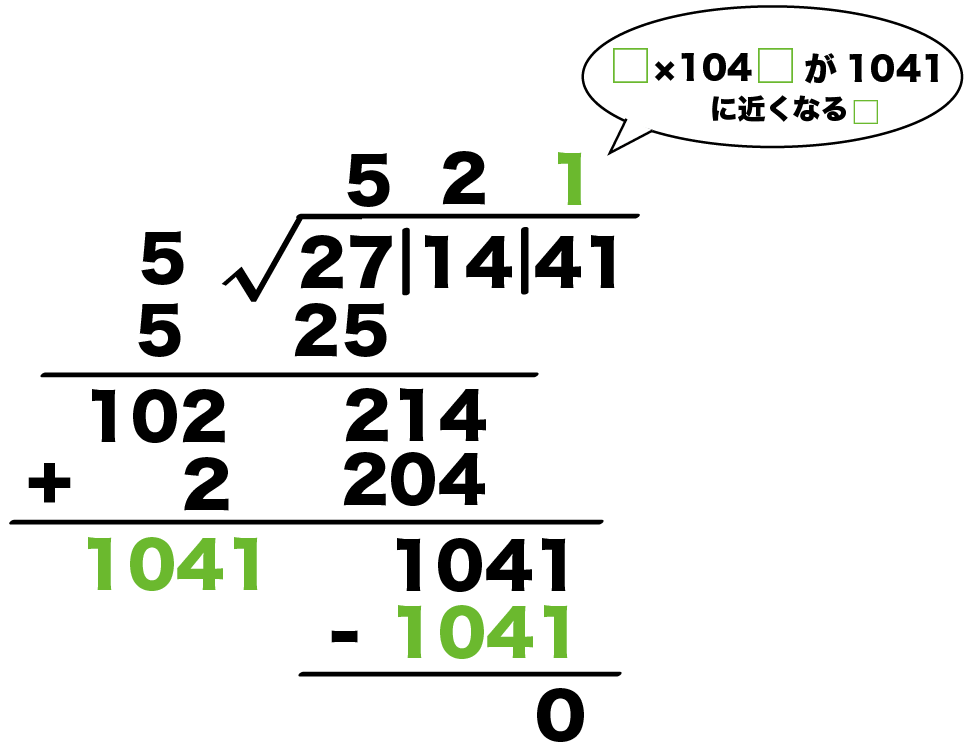
よって、これで筆算の平方根の求め方は終了だ。
271441
の平方根はそのうえの数字の「521」だよ。
やったね。

13ステップは長すぎるぜ^^
まとめ:筆算をつかった平方根の求め方は辛い
平方根の求め方に筆算をつかうと、
- でかい数の平方根を求めるとき
- 小数点以下のケタ数をだしたいとき
- 小数の平方根をだしたいとき
で便利だったね??
ただ、その求め方は阿修羅の道。
訳のわからないプロセスを延々と続けることになるw
もしもに備えて筆算もマスターしておこう。
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。

























この方法は、小数点での計算の時にも使えますか?(5.67など)
どうだろ!小数点の計算は学校で習った筆算がいいね!
小数点以下も、2つづつ塊にするだけ。
あと、00を下におろして繰り返せば、小数点以下何桁でも無限に求められる。
これは面白い。奇数桁の場合は、①、②、②、②…って区切りになるんですね。
試しに168でやってみたら12で終わったんだが…12.958にたどり着かない
凄い!!!!
こんな方法があるなんて…
√2でやりましたんですけど1の位が4になりました
匿名より 様へ
1の位の2が何に一番近いかというと、
①0*0=0
②1*1=1
③2*2=4
で、1が一番近いことが分かります。だから1の位は1です。
難しい、、、たくさんやるしかないですね!
むずい
これテストでた。
訳分からなかった。