扇(おうぎ)形の面積の求め方の公式を簡単に覚えたい!
こんにちは、この記事をかいているKenだよー。コーヒーは何度飲んでもうまいね。
「円とおうぎ形」という単元では、
- 円
- おうぎ形(扇形)
という2つの図形について勉強していくよ。

前回まで、
っていう2つの公式をマスターしてきたね。
今日は、「扇形の面積」について詳しく勉強していこう。
「面積の求め方の公式」をおぼえていればテストでも楽勝さ。
~もくじ~
- 扇形の面積の求め方の公式
- なぜ公式がつかえるのか??
一生使える!扇形の面積の求め方の公式!
「おうぎ形の面積の求め方」はつぎの公式であらわされるんだ。
半径をr、面積をS、円周率をπ、中心角をαとすると、
S = πr² × α / 360
になるんだ。

つまり、
円周率×半径×半径×中心角÷360
ってわけさ。
たとえば、半径3cm、中心角が90度の扇形があったとしよう。扇形の公式をつかってやれば、
S = 3×3×π×90/360
= 9π/4

になるんだ。どんな扇形の面積でもバッチコイだね!!
扇形の面積の公式ってなんでつかえるの??
扇形の面積の求め方はあんまり難しくない。シンプルさ。
ただ、半径rの「円の面積」に「おうぎ形パワー」をかけているだけなんだ。

ここでいう「おうぎ形パワー」っていうのは「扇形の大きさ」をあらわしている指数のことさ。
扇形が大きければ大きいほど大きくなる。
おうぎ形パワーとは、
「同じ半径の円」に対して「扇形」がどれくらいの割合になっているか??
ということを表したものなんだ。
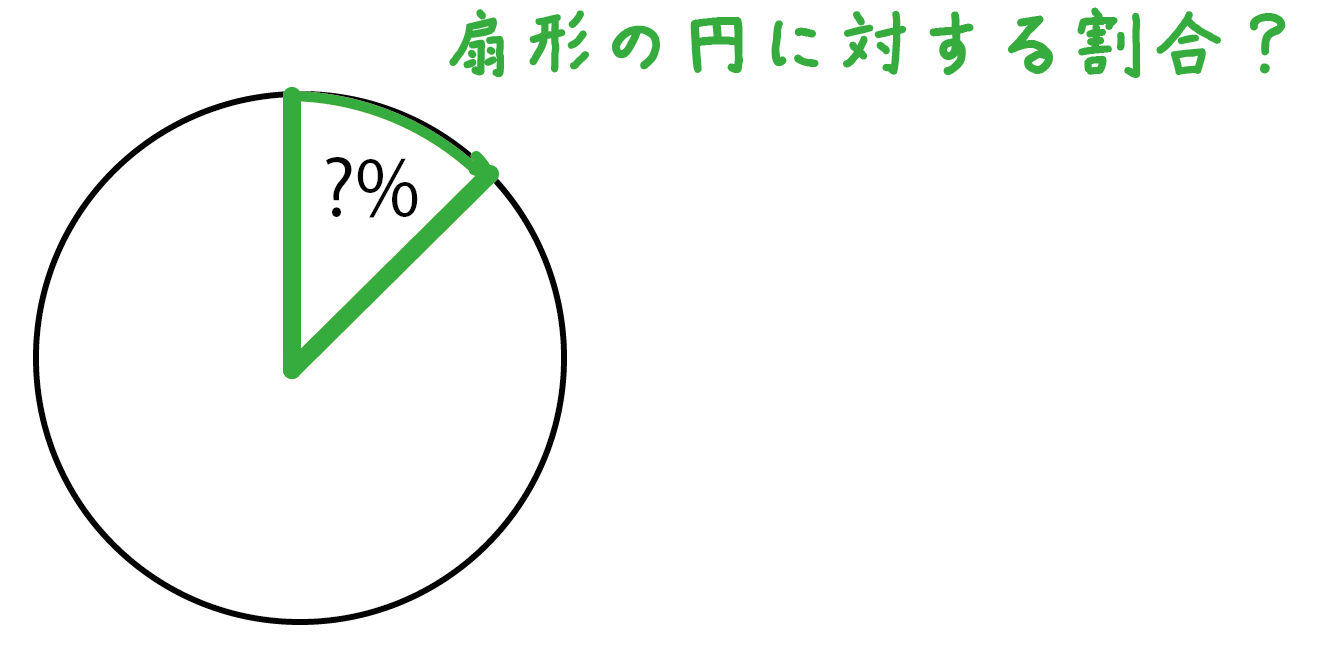
この割合を計算するためには、
「扇形の中心角」が360°中どれだけ大きいか??
ということをみればいい。だって、円の中心角はぐるっと回った360°だからね。
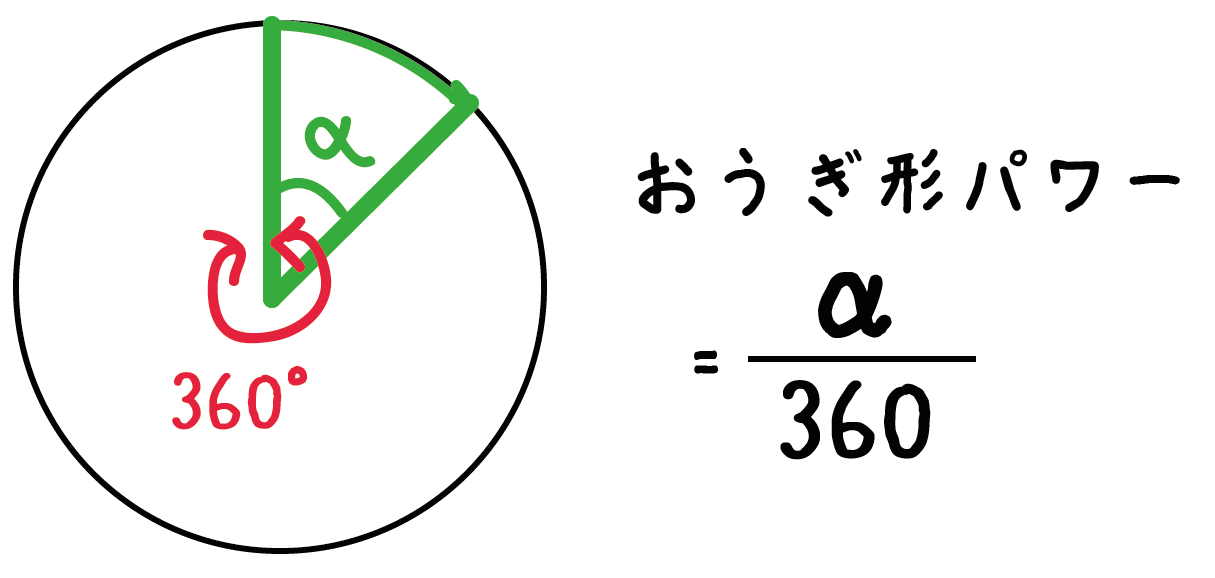
だから、おうぎ形パワーは中心角αを360°でわった、
α/360
になるんだ。
これはなんという偶然か、ピザを切り分けるときと一緒。
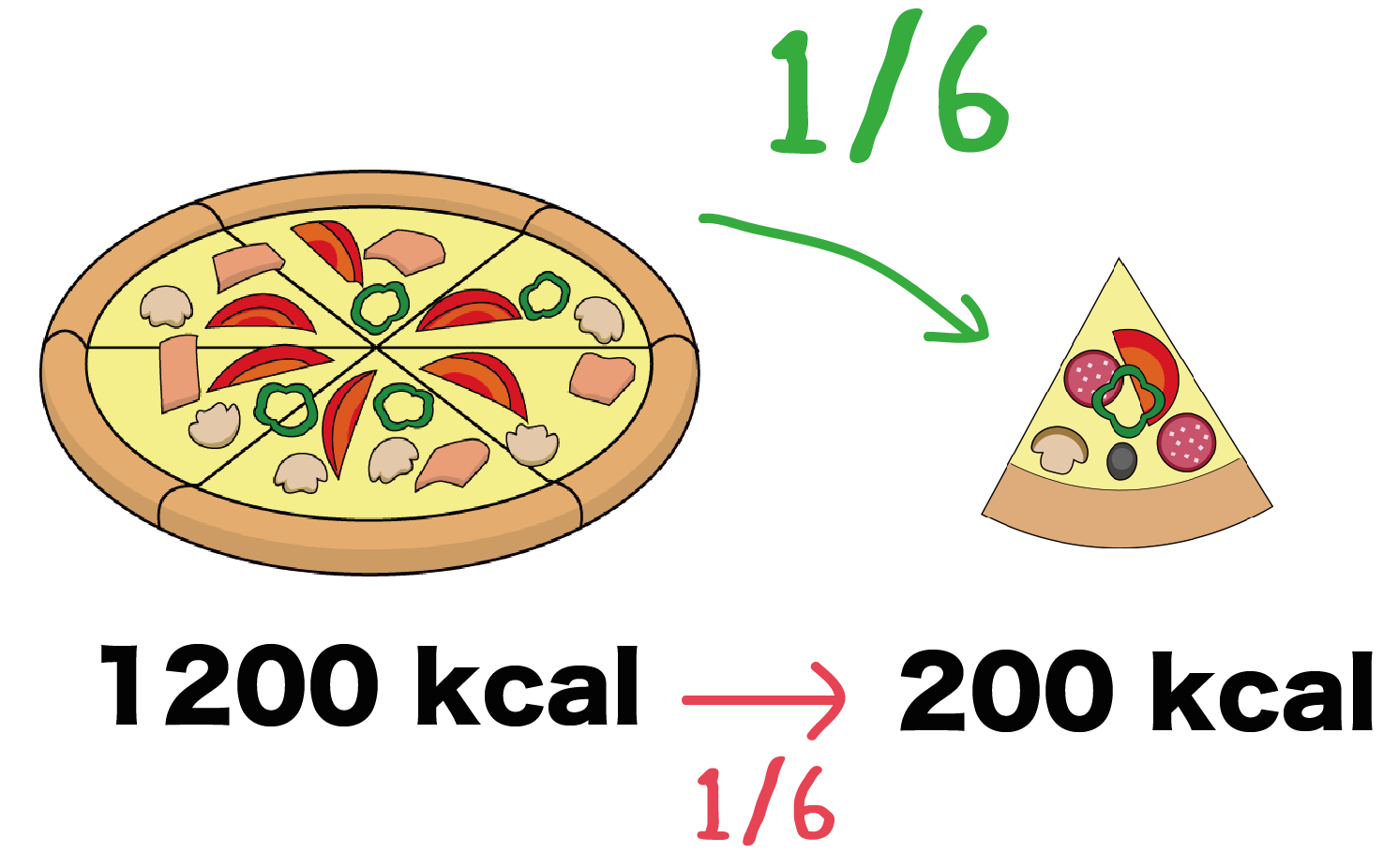
一枚まるまる1200kcalのピザがあったとしよう。こいつを6枚に切り分けると、カロリーはその1/6の200kcalになるでしょ??
これは一枚のピザにたいしてどれぐらいの大きさをしているか、ということを表しているんだ。
「扇形の面積の公式」を忘れたら「ピザ」を思い出そう笑
まとめ:扇形の面積は「おうぎ形パワー」を円にかける
扇形の面積の求め方はどうだった??
円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。
S = πr² × α / 360

「円とおうぎ形」がテストにでるときに確認したいね^^
おうぎ形の面積をマスターしたら次はおうぎ形の中心角を求めてみよう!
そんじゃねー
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。
























おうぎ形の面積の問題で360分のaのところですが、aが判明していない問題がありました。分かっているのはおうぎ形の半径が6センチということと、底面積の円の半径が4センチということだけです(円錐です)。どうやって解けばいいのでしょうか?
まずは中心角aを出してみよう。
(底面の円の円周の長さ)=(扇型の弧の長さ)
っていうaに関する方程式を作ってみて!
詳しくは「円錐の表面積の求め方」を読んでみてね〜
とてもわかりやすくていいと思います。
解けなかった問題が解けるようになってとても助かりました。
ありがとう!
中心角が分からなくて、半径と弧の長さが分かる場合面積はどういう式で求めるのですか?
中心角と弧の長さは分かるけど、半径が分からない時の式も教えてください!
>中心角が分からなくて、半径と弧の長さが分かる場合面積はどういう式で求めるのですか?
半径と弧の長さから中心角を出してみよう!
中心角をxとして方程式作るといいよ
>中心角と弧の長さは分かるけど、半径が分からない時の式も教えてください!
これは半径をxとして方程式を作ってみよう。
α/360の扇形パワーについてなんですけど、これってもしかして扇形の弧の長さについても同じように考えられませんか!?
扇形の弧の長さをlとしたら、360°は2πrに対応して
l/2πrも扇形パワーとして捉えることができませんか!?
底面の半径が6センチ円錐を、頂点Oを中心として、すべらないように平面の上を転がすと、円錐はちょうど2回半回転して、もとの位置にもどった。このとき、円錐の側面となるおうぎ型の中心角の大きさは何度か?っという問題の解き方を教えてください!
もう数学が嫌すぎて
萎えてます
どうしたらいいでしょう …⤵︎⤵︎⤵︎
>α/360の扇形パワーについてなんですけど、これってもしかして扇形の弧の長さについても同じように考えられませんか!?
扇形の弧の長さをlとしたら、360°は2πrに対応して
l/2πrも扇形パワーとして捉えることができませんか!?
そうだね!笑 扇型パワーは円に対する扇型の割合だから、弧の長さでも使えるね!
>底面の半径が6センチ円錐を、頂点Oを中心として、すべらないように平面の上を転がすと、円錐はちょうど2回半回転して、もとの位置にもどった。
このとき、円錐の側面となるおうぎ型の中心角の大きさは何度か?っという問題の解き方を教えてください!
まずは図をかいて整理してみよう。
2回転半したってことは、この円錐が描いた大きな円の円周の長さが、底面の円周の2.5倍ってことだ。
このことから、円錐が描いた円の直径を求めてみよう!
半径と円周は分かっていて、中心角が分からない問題があります。
その場合、中心角を求めると思うのですが、中心角はどう求めたらいいんですか?
>もう数学が嫌すぎて
萎えてます
こんなことを言うのもあれだけど、
他に好きなことがある場合は数学をやらないって言う選択肢もありだと思う!笑
でも、まだQikeruで頑張ってみようぜ!
>半径と円周は分かっていて、中心角が分からない問題があります。
その場合、中心角を求めると思うのですが、中心角はどう求めたらいいんですか?
中心角をxとして、円周に関する方程式を立ててみよう。
半径×半径×中心角÷360 = 扇型のこの長さ
点Oを中心として半径2センチの円を書きなさいと書いてあった問題があってわかりません。図には点Oしか書いてないので教えてください。
>点Oを中心として半径2センチの円を書きなさい
コンパス使っちゃダメなの?笑
おうぎ型の解き方が曖昧でしたが、わかりやすい解説で、しっかり覚えられました。(ありがとうございます)
とてもわかりやすいですね。
いつもありがとうございます
ありがとう!!!
円周を求める公式が 直径×円周率(3.14) ですか?
>円周を求める公式が 直径×円周率(3.14) ですか?
そうだよ。なぜなら、円周率は円周が直径の何倍になってるかを表したものだからね。
直径に円周率をかけると計算できるんだ。
詳しくは「円周の求め方」を読んでみて
弦や弧の意味がいまいち分かりません‼︎
教えてくださいー!!!!!!
>弦や弧の意味がいまいち分かりません‼︎
教えてくださいー!!!!!!
弦は円周上の2点を結んだ線分のことで、
弧は円周の一部のことだ!
ありがとうございます
もうすぐテストなので助かりました!!
自分に自信が持てました!!
ありがとうございます!!!!!
ありがとう!!扇型を制覇しよう!
わかっているのは、弧の長さ3/2πcmと半径6cmの扇形の面積をまとめなさい。という問題がありますが、どうやって解けばいいのかよくわからないので、教えてください!明日テストです。
どうしてa/360になるのか
先生に説明しろっていわれて
わからないんですけど
どーしたらいいですか?
>弧の長さ3/2πcmと半径6cmの扇形の面積をもとめなさい
これは中心角をxとして、孤の長さに関する方程式を作ってとく問題だ。
中心角がわかったら、扇型の面積の公式に当てはめればいいね
半径の求め方知りたい
弧の長さを求めるとき、πに×2されているのに
面積を求めるとき、πに何もされてないのはなぜ?
>どうしてa/360になるのか
先生に説明しろっていわれて
わからないんですけど
どーしたらいいですか?
円と扇型の中心角の比だね!
>半径の求め方知りたい
中心角と弧の長さがわかっていたら、半径をrとしてこの長さに関する方程式を作ってみよう
>弧の長さを求めるとき、πに×2されているのに
面積を求めるとき、πに何もされてないのはなぜ?
弧の長さの計算は直径をかけるから、半径を2倍して直径にしていたんだ。
逆に、面積の場合は半径のままでいいか何もしないのさ
円すいの展開図について…
扇形の中心角の大きさを求める問題が答え見ても
さっぱりです!
どーやって解くか教えてください!!
>円すいの展開図について…
扇形の中心角の大きさを求める問題が答え見ても
さっぱりです!
どーやって解くか教えてください!!
扇型の中心角の求め方を読んでみて!
半径3㎝で中心角が90度の扇形OABがあります。
この扇形OABを、線分AOを軸として1回転させてできる立体の体積を求めなさい。
ただし、円周率はπとします。
という問題が分かりません。
どうやって解くのか教えて下さい。
>半径3㎝で中心角が90度の扇形OABがあります。
この扇形OABを、線分AOを軸として1回転させてできる立体の体積を求めなさい。
ただし、円周率はπとします。
という問題が分かりません。
まずは回転してできる立体の見取り図をかいてみよう。
詳しくは「回転体」の記事を読んでみて
中心角をださなくても1/2×孤の長さ×半径でも良いですよね?
扇形O-AB⌒があり、辺OAの中点がCで辺OBの中点がDとしていて、
扇形O-CD⌒ができて、扇形O-AB⌒と扇形OCD⌒の面積比が何故
四倍になるんですか?
>扇形O-AB⌒があり、辺OAの中点がCで辺OBの中点がDとしていて、
扇形O-CD⌒ができて、扇形O-AB⌒と扇形OCD⌒の面積比が何故
四倍になるんですか?
面積比は相似比の2乗になるよ。
なぜなら、面積を計算するために辺を2回かけるからね
中心角を求める問題がとことんできません。どうやって求めるんですか?
暗記がとことん苦手で、公式を覚えられません。簡単に覚えられる方法はありますか?
周の長さ5πcmしか、分からない状態で半径と面積はどうやって求めるんですか?(特に半径がよく分からないです;;)
>暗記がとことん苦手で、公式を覚えられません。簡単に覚えられる方法はありますか?
公式は使って覚えるのが一番。
最初は公式を見ながらでもいいから解いて、たくさん問題を解いているうちに公式が染み込んでくるはずだ
>周の長さ5πcmしか、分からない状態で半径と面積はどうやって求めるんですか?(特に半径がよく分からないです;;)
扇型の周りの長さは図をかいてみるとわかるけど、
半径+半径+弧の長さ
になってるね。だから、半径をrとして周りの長さに関する等式を作れそうだね
大きな半円の中に小さな半円が2個あり
微妙に重なってて、その部分を除いた部分の
面積を求める問題。
教えてください。
すごく分かりやすくいつも助かってます!!
頑張って下さい!
ありがとう!!
非常にわかりやすい!
ありがとう!!
円Oの周上に3点A、B、Cがある。
円Oの半径が6cm、点Aを含むおうぎ形OBCの中心角が210度のとき、点Aを含まない弧BCの長さは何cmか。
この答えが5πcmになるのですがなぜそうなるのかが分かりません。教えてください!
>円Oの周上に3点A、B、Cがある。
円Oの半径が6cm、点Aを含むおうぎ形OBCの中心角が210度のとき、点Aを含まない弧BCの長さは何cmか。
この答えが5πcmになるのですがなぜそうなるのかが分かりません。教えてください!
Aを含まない側の扇型OBCの中心角を求めてみよう。
あとは扇型の弧の長さの公式で計算するだけ!
よく分かりました!✌もうすぐ学年末なので、範囲が広くて困っていま でもkenさんのおかげで分かりました❗本当にありがとうございます
よかった!!頑張ろうぜ!!
暗記するコツを教えてください
>暗記するコツを教えてください
繰り返しめげずにやるかな笑 自分を信じることも大事
今ちょうど、わからなくて困っているところでした!ありがとうございます!これでわかりました!
半径2センチで中心角が210度の大きさのおうぎ形の書き方が分かりません
>半径2センチで中心角が210度の大きさのおうぎ形の書き方が分かりません
半径をかいて、中心角210度を分度器で測って反対側の半径をかいてコンパスでこを書こう
半径10㎝、中心角90°扇形の周上を、半径2㎝の、円が1周します。
円が、通過する部分の周りの長さ
円が通過する面積
>半径10㎝、中心角90°扇形の周上を、半径2㎝の、円が1周します。
円が、通過する部分の周りの長さ
円が通過する面積
これは難しい。
円が移動する様子を図にかいてみるといいよ。あとは地道に計算していくだけだ
半径が6cmの扇形OABです。これについて、次の問いに答えなさい。ただし、円周率はπとします。
扇形OABの面積が8πcm²のとき、xの値をと求めなさい。(xは角度です)
の求め方教えてください!
>半径が6cmの扇形OABです。これについて、次の問いに答えなさい。ただし、円周率はπとします。
扇形OABの面積が8πcm²のとき、xの値をと求めなさい。(xは角度です)
半径x半径x中心角÷360 = 8π
という方程式を解いてみようぜ
扇形の問題で教科書の文をそのまま失礼します!
OA=10cm OB=40cmとします。線分ABを、点Oを中心として時計回りに120°だけ回転移動させるとき、線分ABが動いたあとにできる図形の面積を求めなさい。←これが全然わかりません。求め方を教えてください泣
>OA=10cm OB=40cmとします。線分ABを、点Oを中心として時計回りに120°だけ回転移動させるとき、線分ABが動いたあとにできる図形の面積を求めなさい
まずは作図してみよう!
120度時計回りに回転させた時のAとBの位置をA’、B’としてかいてみようぜ
今までで一番分かり易いサイトですー
良く頭に入りました!!
ありがとう!!
そうですね!
めっちゃ写して頭叩き込めました
わかりやすかったです!
ありがとうございます。
おお!よかった!!
おうぎ形の角はどうやって求めるんですか?
とっても分かりやすかったです!ありがとうございます!頑張って下さい!
扇型の中心角の求め方を読んでみてね
半径7cm、弧の長さ4πcmのおうぎ型の面積はどう求めたらいいですか?
まずは扇形の中心角を求めるといいね!
S = πr^2 × α / 360の「^」って何でしょうか(・・?
「^2」で「2乗」の意味だよ!わかりづらいから修正しておきました!
公式、覚えられませーん(._.)
”ごろあわせ“とかないですかー?
いつもわかりやすいです!問題が解けました!
2πrじゃないんですか?
扇形の面積は三角形の公式が使えると友達が言っていたんですが、なぜですか?
扇型から扇型を引くやつもやってください
鈍角三角形や鋭角三角形の面積の公式を教えてください。
π*8*8*3.15/365
のような分数に小数が入ってる場合はどうすればいいんですか?
分数で答えよう
半径の長さが分からない時は、どうすればいいですか?
おうぎ形OAB の中心角は45°である。おうぎ形OAB の面積は、円Oの面積は何倍ですか。
という問題があるのですがどう解けば良いのか分かりません
明日、やばいテストなんですよね、、、。
分かりやすくて超助かりました