【中学数学】球の体積の求め方の公式を1発で覚える方法

球の体積の求め方の公式が覚えられねえ！！

こんにちは！この記事をかいているKenだよ。ビニール傘を買っちゃったね。

球の体積の求め方には公式があるんだ。

球の半径をrとすると、体積の求め方は、

$$\frac{4}{3}πr^3$$

になるよ。

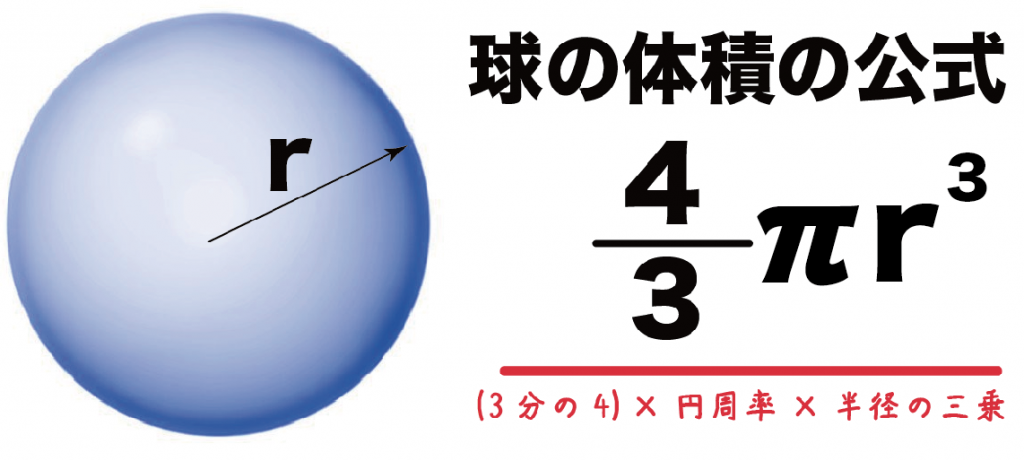
つまり、

3分の4　×　円周率　×  半径　×　半径　×　半径

ってことだね。

この公式でどんなボールの体積も計算できちゃうんだ。

たとえば、半径30 [cm]のサッカーボールがあったとしよう。

こいつの体積は「4/3　×　π　×　半径の三乗」という公式をつかってやると、

になるね。

これってサッカーボールの中にどれぐらい空気が入っているか？ってことなんだ。

ちょっとすごくない笑？

ただ、この公式にも一つだけ欠点がある。

それは、

むちゃくちゃ暗記がむずかしい

ってことさ。

3分の4なんてどっから来た数字かわからないし、半径を何回かけたらいいのかわからない。

これじゃあ球の体積の問題をだされたらやばすぎる・・・・

そこで、今日は、

中学生でもおぼえられる「球の体積の求め方」を解説していくよ。

球の体積の公式を忘れちゃったときに参考にしてみて。

球の体積の公式を1発で覚える方法

「球の体積の公式」を暗記する方法を伝授しよう。

3分の4　×　円周率　×　半径の三乗

という公式はつぎの語呂を使えばおぼえられちゃうよ。

さんしろう、おいしいパイを持ってある日参上

えっ。

あ、大事だからもう一度繰り返すよ。

さんしろう、おいしいパイを持ってある日参上

なぜこの語呂で「球の体積の公式」おぼえられるのか。

それは、

さんし（3分の4）ろう、美味しいパイ（π）を持ってある（r）日参上（三乗）

になるからさ。

つまり、

• 「さんしろう」→「$\frac{4}{3}$」
• 「おいしいパイ」→「π」
• 「ある日」→「r」
• 「参上」→「三乗」

という感じで、それぞれの言葉が対応してるってわけ。

だから、

さんしろう、美味しいパイを持ってある日参上

という語呂を覚えてしまえば「球の体積の求め方」の公式も一生忘れないってことさ。

おめでとう！！

まとめ：中学数学の「球の体積の公式」は語呂で制す

中学数学では「球の体積の公式」が使える理由がわからない。

完全に理解するためには「積分」という知識を使わなきゃいけないんだ。

だからこそ、中学生の間は、

さんしろう、美味しいパイを持ってある日参上

という語呂で「球の体積の公式（3分の4　×　円周率　×　半径の三乗）」をおぼえてしまおう。

テスト前にがんばって暗記してみてね^^

そんじゃねー

Ken
なぜ球の公式がつかえるのか気になったらみてみて↓

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。