直角三角形の比は3つ覚えればいい??
こんにちは!ぺーたーだよ。
三平方の定理で覚えておきたいのは、
直角三角形の比
だよ。
これを覚えておけば、
三平方の定理を使わなくて辺の長さを計算できちゃうんだ。
楽に解けるんなら知っておきたいよね?
んで、そのパターンは全部でつぎの3つ。
- 30、60の直角三角形
- 45の直角三角形
- 3 4 5の直角三角形
覚えるだけで簡単に三平方の定理の計算問題が解けるよ。
覚えると便利!直角三角形の3つの比
それじゃあ早速、中学数学の問題でよく出てくる、
直角三角形の辺の比
を3つ紹介するよ。
比その1. 「1 : 2 : √3」
まず覚えておいておくべき直角三角形の辺の比は、
1:2:√3
だよ。
この辺の比になる直角三角形の角度は、
- 30°
- 60°
- 90°
になってるんだ。

例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。

このとき、残りの辺のABとACは、1:2:√3の辺の比を使うと、
- AB = 2BC = 4 cm
- AC = √3BC = 2√3 cm
になるのさ。

えっ。
このタイプの直角三角形をどこかでみたことある??
実はこれ、三角定規の直角三角形のうちの長い方だね。

正三角形を半分にした形って覚えてもらえればいいかな。

中学数学の問題では3秒に一回ぐらい使う直角三角形の辺の比だから、
確実に覚えておこう。
比その2.「1:1:√2」
次の直角三角形の辺の比は、
1 : 1: √2
だよ。
これは直角三角形の角度がそれぞれ、
- 45°
- 45°
- 90°
の奴なんだ。

内角のうちの2つの角度が等しいから、
ってわけね。
辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。
たとえば、次の直角二等辺三角形ABCにおいて、 BC=5cmとすると、
残りの辺の長さは、
- AC = BC = 5 cm
- AB = √2BC = 5√2 cm
になるよ。

えっ。この直角三角形をどこかでみたことあるって!??
そう、そうだよ。
三角定規のもう片方の小さい奴なんだ。

んで、もっというと、
正方形を半分にした形だよ。

この比もよく使うからおぼえておいてね!
比その3. 「3 4 5 の直角三角形」
最後の直角三角形の辺の比は、
3 : 4: 5
だよ。

たとえば、斜辺以外の辺の長さが6cm、8cmの直角三角形ABCがあったとしよう。

この直角三角形の2辺の長さを比べてみると、
6: 8
つまり、
3: 4
になってるよね??

ってことは、この三角形は3: 4: 5の直角三角形ってことがわかるね。
BC : AB = 3 :5
になってるはずだから、
ABはBCの3分の5倍だね。
よって、
AB
= BC× (3分の5)
= 10 [cm]
になるね。

3 4 5の直角三角形の比もよく出てくるからしっかり押さえておいてね。
>> 詳しくは「3: 4: 5の直角三角形の問題の解き方」を読んでみて^^
まとめ:直角三角形の比3つを使い倒せ!
中学数学でよく使う直角三角形の比は次の3つ。
- 30、60の直角三角形
- 45の直角三角形
- 3 4 5の直角三角形
これを覚えるだけで三平方の定理を使わなくてよくなるから、
だいぶラクになるね。
いきなり覚えるのはむずいけど、使いながら覚えてこうね。
それじゃあ、また
ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める

















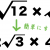











直角三角形で3 4 5の他に三ぺんが
整数になるのはあと何があるのですか?
>直角三角形で3 4 5の他に三ぺんが
整数になるのはあと何があるのですか?
5・12・13もあるよ!
7,24,25もあるよ!
3たい4たい5以外には何もないのですか?
>3たい4たい5以外には何もないのですか?
5:12:13もよくでるね!
>3たい4たい5以外には何もないのですか?
1118, 1680, 2018 の直角三角形も雑学程度に覚えよう!
直角三角形の各辺を1辺とするA,B,Cの正方形があります。Aの面積は324cm2、Bの面積は144cm2のとき、正方形に接する直角三角形の面積は何cm2ですか。
>直角三角形の各辺を1辺とするA,B,Cの正方形があります。Aの面積は324cm2、Bの面積は144cm2のとき、正方形に接する直角三角形の面積は何cm2ですか。
A、Bの面積からそれぞれ一辺の長さを求めてみよう。
あとはその一辺たちを持つ直角三角形の面積を計算すればいい
三平方の定理とは何ですか。あと1:1:なに2と書かれているんでしょうか。
ルート2だね!平方根ってやつ
同じ大きさの正方形へを3つ並べて横に並べて、正方形2つでできる長方形の対角線を引いてできる小さな角と正方形を3つ並べてできる長方形の対角線を引いてできる小さな角の和は、45度になりますがどうしてですか。教えてください。
15°の傾斜を 2,000m進むと高さは何mでしょうか?