【中2数学】一次関数の切片を求める2つの方法

一次関数の切片を求めたいんだけど？？

こんにちは！この記事をかいているKenだよ。自転車、ほしいね。

一次関数の切片（せっぺん）ってなんだろう？？

よく耳にするけど、イマイチわからないよね。

教科書をみてみると、

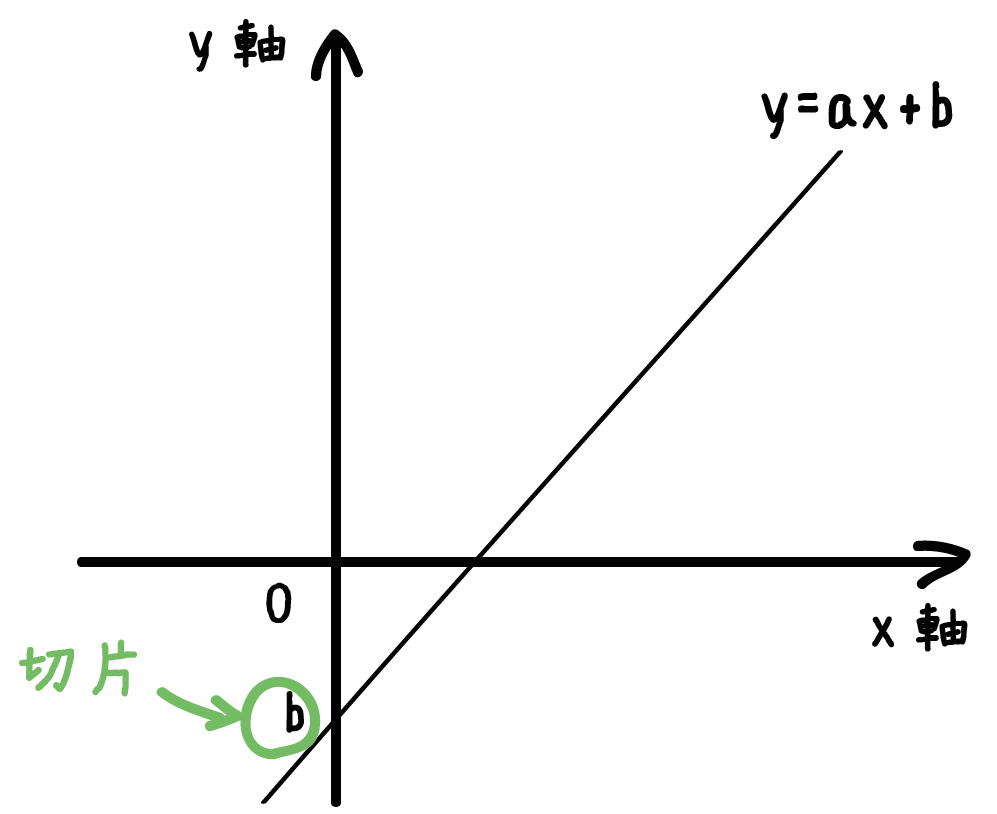
直線y = ax+bとy軸との交点（0, b）のy座標bを、この直線の切片といいます。

ってかいてある。

正直ちょっとよくわからない。

コイツをわかりやすくいうと、

「1次関数」と「y軸」がまじわっている点の「y座標」ってことだ。

「せっぺん」って名前は取っ付きにくいけど、

意外とわかりやすいヤツでしょ？？笑

今日は「切片」の求め方を2つ紹介していくよ。

よかったら参考にしてみてね^_^

一次関数の切片がわかる2つの求め方

つぎの2つの求め方でゲットできるよ！

求め方1. 　計算式「y= ax + b」から読み取る方法

一次関数の中で「xでもyでもない項」をさがす方法だ。

数式見るだけで切片が求まるから簡単だね。

一次関数 y = ax + b の切片はずばり、

bの値

だ。

どんなにひねれくれていて、複雑な一次関数でも同じ。

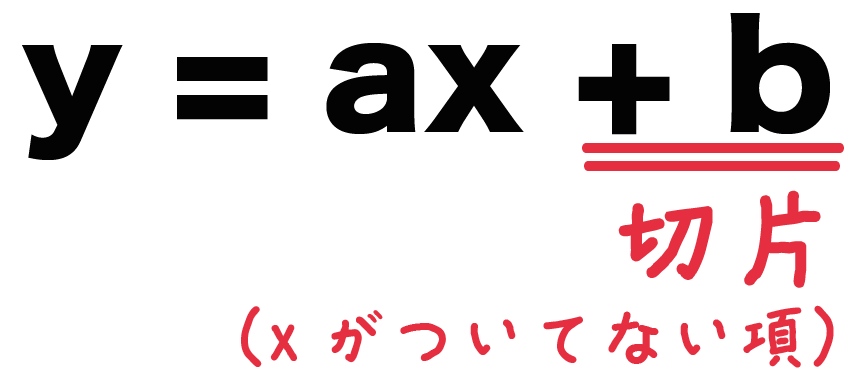
ってことは、

xもyもついていない項が切片

って言えそうだね。

だから、この「bの値」を数式からみつけてあげればいいわけさ。

たとえば、つぎの例題があったとしよう。

例題

直線 y = 7x – 2の切片を求めなさい。

切片は、一次関数で「xもyもついていない項」のことだったよね？？

ってことは、

y = 7x – 2

で「xもyもついていない項」って「-2」だ。

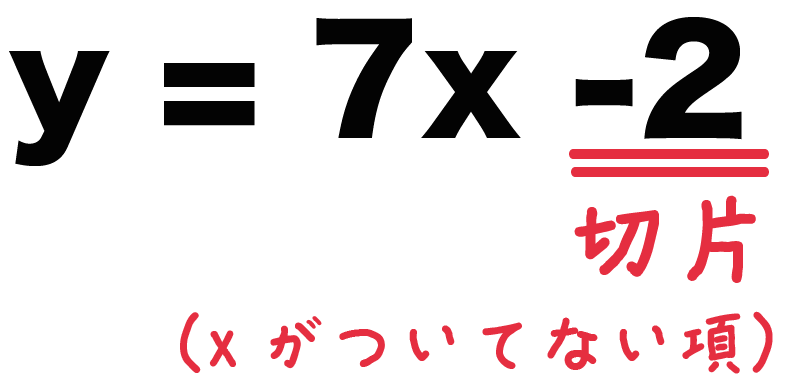
え。

そうそう。

つまり、

1次関数「y = 7x -2」の切片は「-2」なのさ。

グラフをかかなくても切片がわかるなんて便利でしょ？？

求め方2.「 一次関数のグラフでy軸の交点をみつける」

グラフから切片を読み取る方法だ。

これはいたって簡単。

1次関数の直線がy軸とまじわっている点が「切片」だから、

交点をみつけるだけでいい。

ぶっちゃけ、1秒もかからないね。

たとえば、つぎのような問題だ。

例題

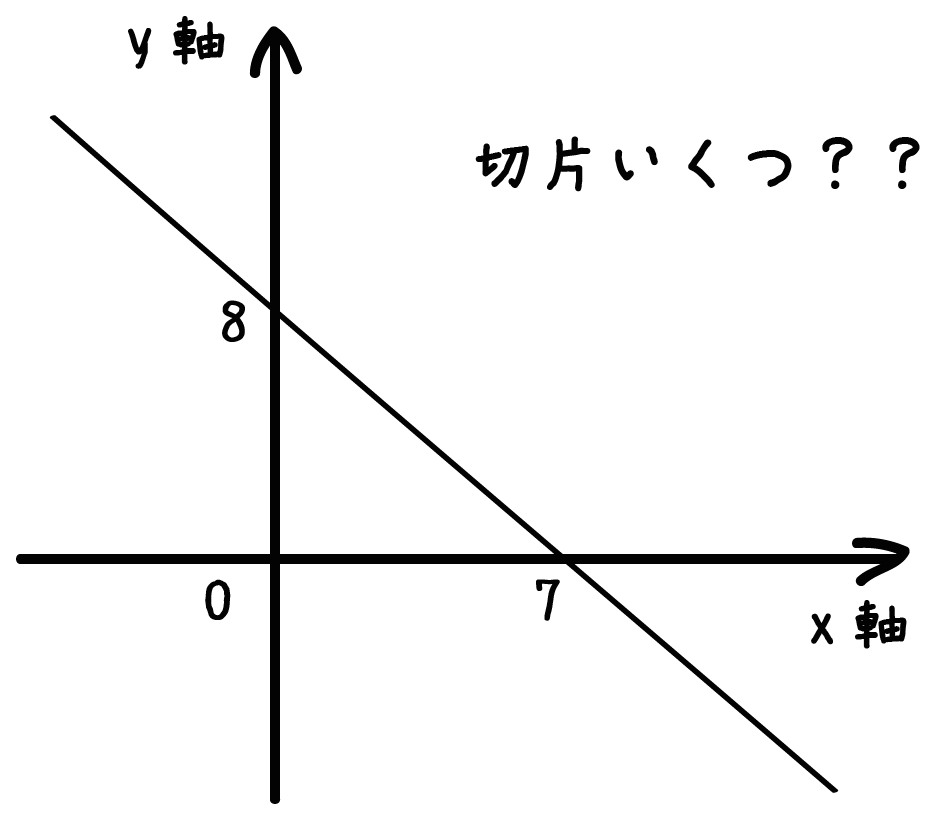
つぎのグラフの一次関数の切片を求めなさい。
※　x軸との交点（7, 0）、y軸との交点(0, 8)

さっきも復習したけど、

切片って、

「1次関数」と「y軸」の交点の「y座標」のこと

だったよね？？

グラフをみてみると、

y軸との交点は（0, 8）ってことがわかる。

だから、この関数の切片は「8」になるね。

なぜなら、交点のy座標は8だからね。

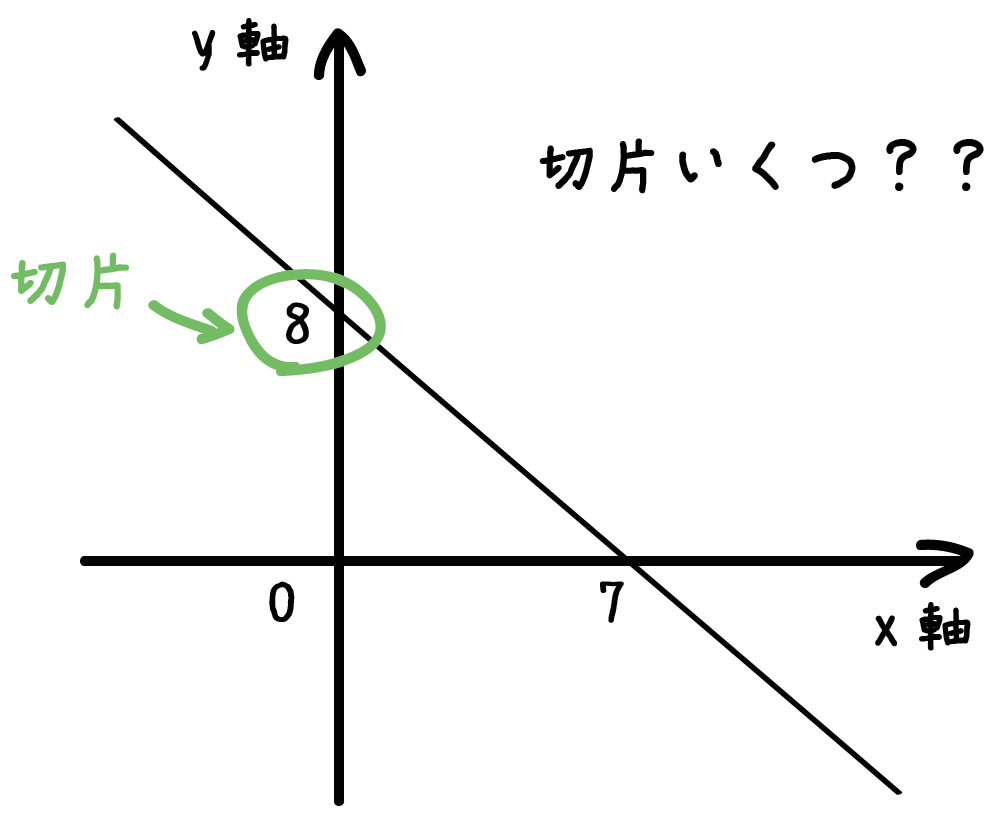
グラフをみるだけで切片がわかる。

チョー簡単な方法だね^^

まとめ：一次関数の切片は2秒ぐらいで求められる

1次関数の切片は意外と簡単。

1. 計算式から読み取る方法
2. グラフから読み取る方法

の2つでガンガン攻略できるよ。

あとはテスト前に問題に慣れておこう！

そんじゃねー

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。