比例定数の求め方がよくわからない!!
こんにちは、この記事を書いているKenだよー!
比例の式を攻略するためには「比例定数の求め方」が必要だ。
比例定数を求めておくれ^^
って直接きいてくる問題は少ないけれど、
xとyの関係を式に表しなさい
って間接的にきいてくる問題が多いんだ。この問題に「比例定数」って言葉はでてこないけど、じつは比例定数の求め方を知らないと解けない。
だから、
比例定数の求め方を知っておいたほうがテストで有利なんだ。

だから今日は、
比例式の「比例定数の求め方」をわかりやすく解説してみたよ。
数学の試験前に確認してみてね^^
~もくじ~
- いちばんカンタンな比例定数の求め方
- なぜこれが使えるのか??
5秒で比例定数が計算できる!超カンタンな求め方
いちばん手っ取り早い比例定数の求め方を紹介するね。
あっ、今回は反比例じゃなくて比例の式の場合だから注意してくれー!
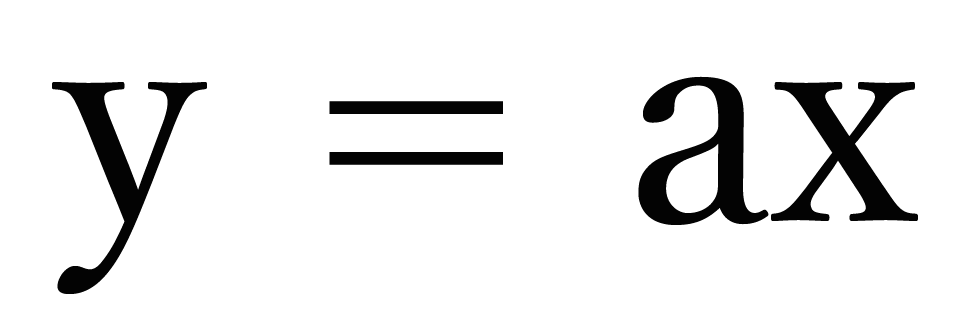
比例の式
上のような比例の式の「比例定数の求め方」は、
yをxで割る(y/x)
ってだけさ。
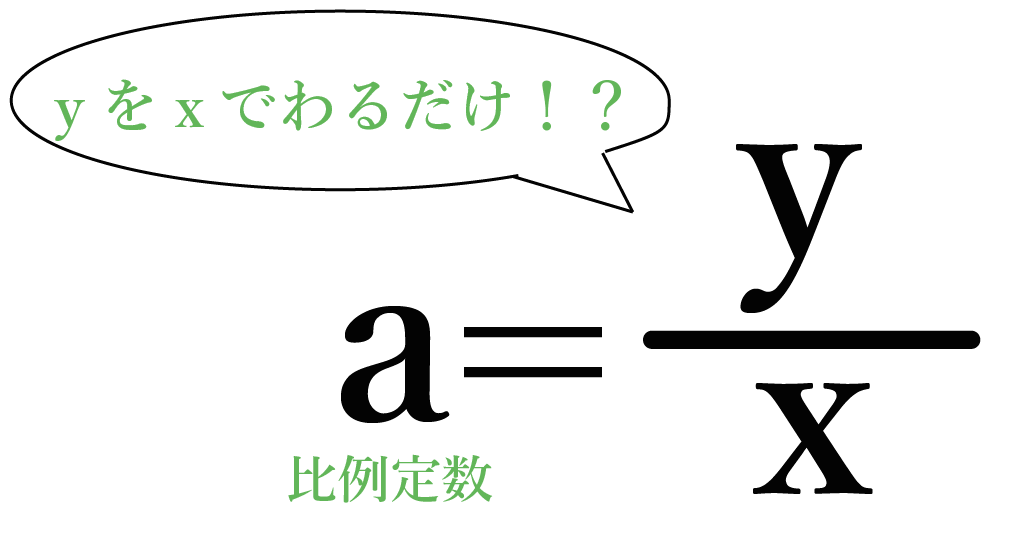
ね?
ものすごくシンプルな求め方でしょ^_^
比例定数を実際に求めてみよう!!
それじゃあ、この求め方で比例定数を計算してみよう!
比例の式で出題されやすいのは次のようなタイプだ。
yはxに比例し、x = 9のとき、y = 54です。xとyの関係を式に表しなさい。
これはちょっとインテリ問題にみえるけど、さっきの比例定数の求め方をつかっちゃえば一発さ。
yとxは比例しているから、
y の値をxでわるだけで比例定数 a が求められるんだ。
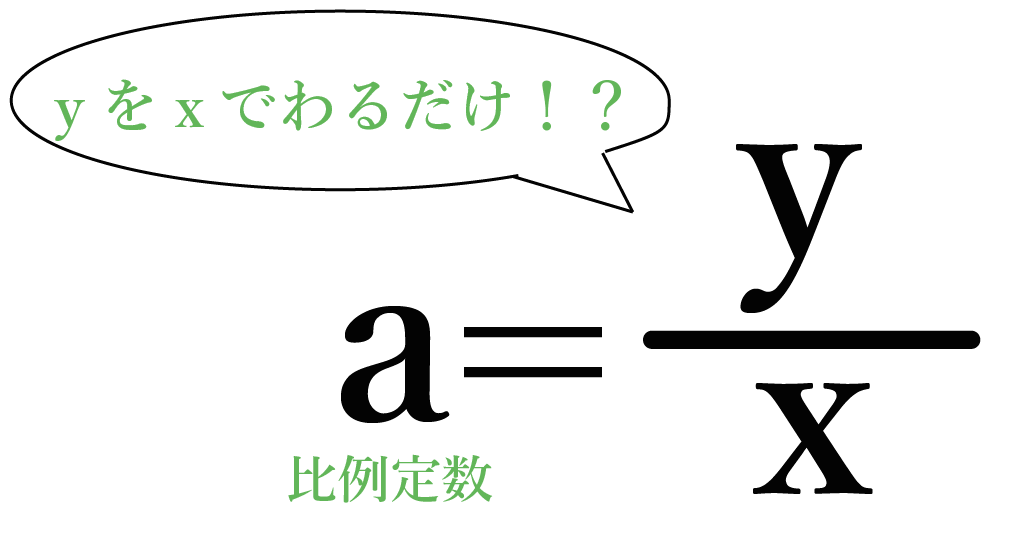
だから、
a = 54 ÷ 9
となって、
a = 6が正解だね。
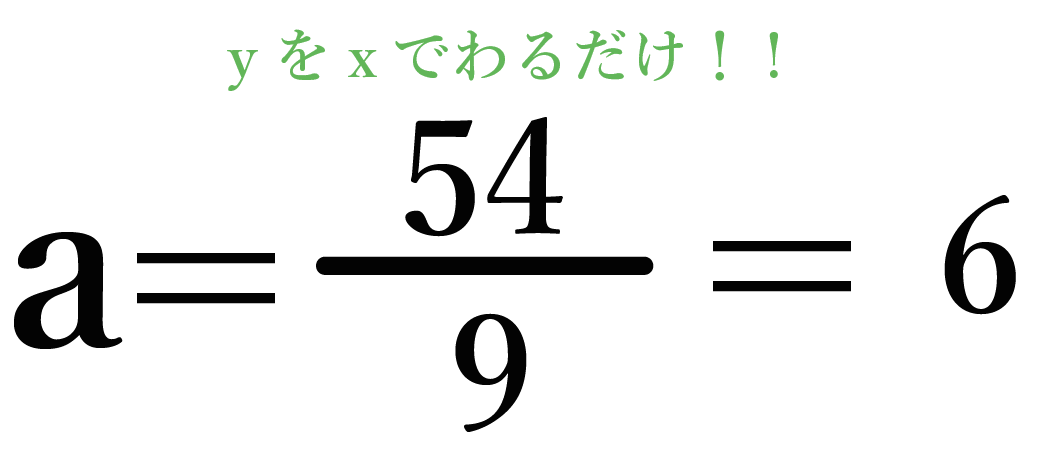
ね? 割り算が得意だったら5秒ぐらいで比例定数がわかるでしょ??笑
比例定数aが6ってでたから、xとyの関係は、
y = 6x
になるね。y = axに求めたaをいれちゃえばいいんだ!
なぜカンタンに比例定数が求められるのか??
yをxでわるだけ
なんてカンタンすぎるよね??
じゃあなんで比例の式の「比例定数の求め方」がこんなにシンプルなんだろうか。
ゆっくりみていけばその理由がわかるよ。
ある関数yがxについて「比例する」ってことは、
y = ax
っていうカタチをした関数ってことだよね?? これは前回の「比例とは??」という記事で勉強したね。
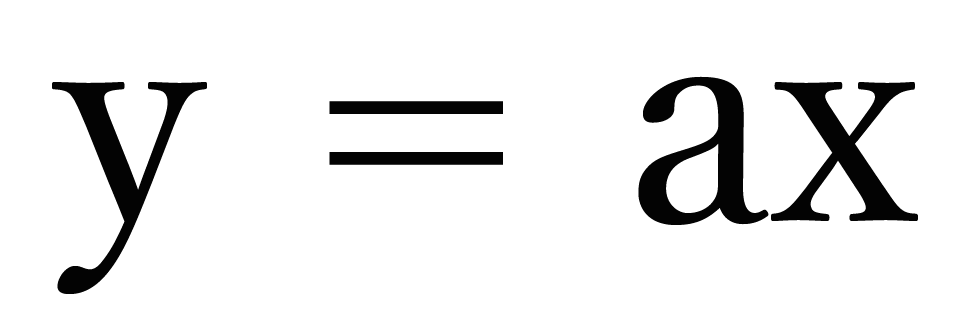
この式をよーくみてみると、
等式であることに気づくよね。だって、左と右が等号(=)でつながれているからね。
そこで、
等式の性質の1つの、
両辺を同じ数でわっても等式は成り立つ
っていうものを使ってみよう。 (忘れかけているときは等式の性質の記事をみてみてね^^)
両辺をxで割ってあげるとこうなって↓↓

右の分子にのった「x」がきえるので、

こうなるね ↓↓
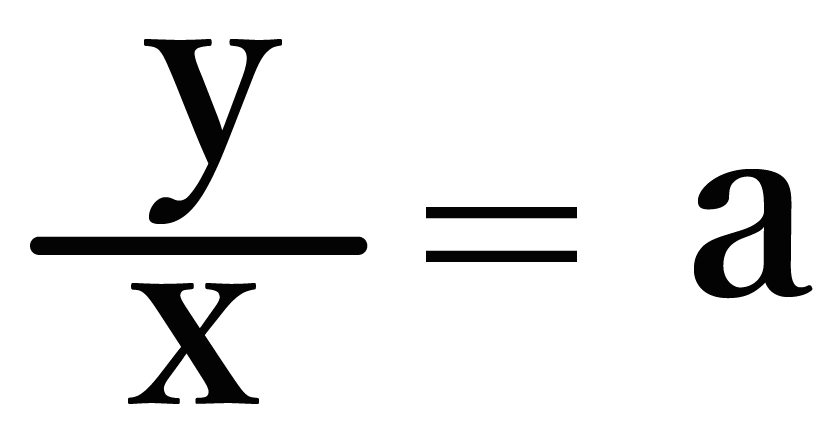
これはいちばん最初にみた、
a = y/xと同じだよね。
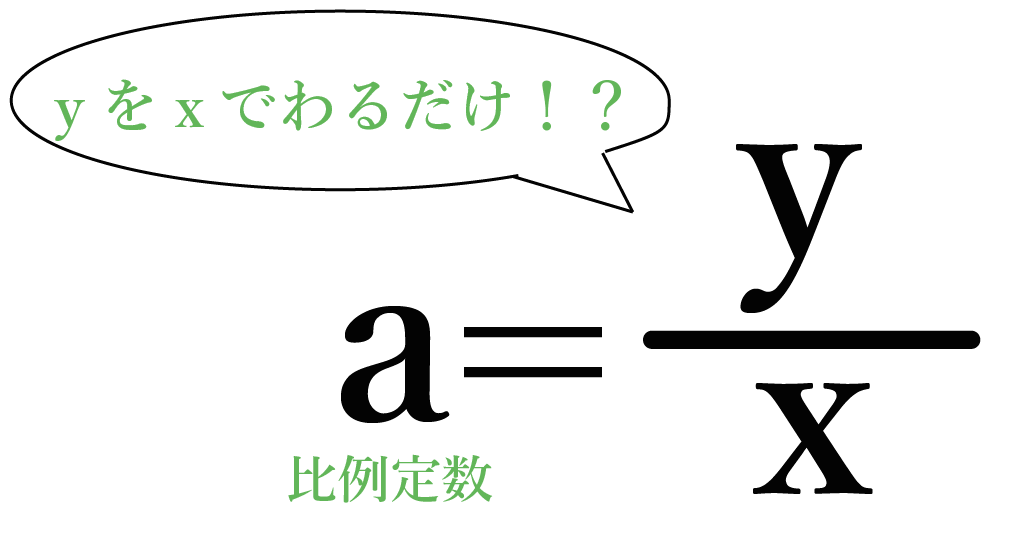
だから、比例の式では、
yをxでわっただけで比例定数aがゲットできるんだ。
どう?? シンプルでしょ??
まとめ:比例の式では「yをxでわる」と比例定数が求められる
yをxでわるだけ!
比例する関数のときは比例定数の求め方はカンタン!
テストでガンガン比例定数を求めていこうね^^
そんじゃねー!
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。




























勉強をしたくてもやる気が起きません。どうすればいいですか??
場所を変えてみたらどうかな?
図書館とか行ってみよう
100個のみかんをx人で等しく分けるとき、1人分の個数はy個になる。
>100個のみかんをx人で等しく分けるとき、1人分の個数はy個になる
わけるときは割り算にすればいいね。
100個のみかんをxで割れば一人分の個数xが出るはずだ
比例と比例定数の違いがわかりません。
周の長さが20cmの長方形の縦の長さをxcm、横の長さをycmとする。
>比例と比例定数の違いがわかりません
比例は関数の種類の名前で、比例定数は比例の関数y=axの「a」のこと。
xが1ふえたらyはいくつ増えるのかってことを表してるよ。
>周の長さが20cmの長方形の縦の長さをxcm、横の長さをycmとする。
長方形の周りの長さは、縦の辺が2つ、横の辺も2つで成り立っているよ。
こいつでうまい具合に方程式をつくってみよう!
x円の物を4個買って800円出すとおつりがy円かえってくるときの、yをxの式で表すのと、比例定数が分かりません。
>x円の物を4個買って800円出すとおつりがy円かえってくるときの、
yをxの式で表すのと、比例定数が分かりません。
払ったお金- 代金 = おつり
だよね?
この通りにxとyの等式を作ってあげよう。
これは一次関数になるっぽいから、y=ax+bのaにあたる数が比例定数だ
yとXの間にy=7xという関係がある時の比例定数を言いなさい。
が分からないです……
>yとXの間にy=7xという関係がある時の比例定数を言いなさい。
比例定数はy=axのaのことだよ。
ってことで、xの前についている数が比例定数だからこの場合でいうと何なるかな?
比例と関数の違いが分かりません
>比例と関数の違いが分かりません
比例は関数の一種だよ。
例えば、比例は柴犬で、関数は犬って感じ
y-x=0は比例式ですか?
>y-x=0は比例式ですか?
比例だね。-xを右辺に移項してみると、y=axの形になるはずだ
方程式のやり方が分りません
教えてください。
>方程式のやり方が分りません
教えてください。
方程式は移項をマスターしておけばどうにかなるね。
一次方程式の解き方を読んでみて
問題ではよく「xをyの式にして求めなさい」などと言う問題が多いと思うんですよ…
それでその問題を解くとしても比例定数っていうのがイマイチわからなくて…
後回しみたいになりましたけど、比例定数って「y=ax」か
「y=a/x(分数)」なのか、どっちが比例定数ですか?
できれば簡単に教えて下さい
>問題ではよく「xをyの式にして求めなさい」などと言う問題が多いと思うんですよ…
それでその問題を解くとしても比例定数っていうのがイマイチわからなくて…
後回しみたいになりましたけど、比例定数って「y=ax」か
「y=a/x(分数)」なのか、どっちが比例定数ですか?
できれば簡単に教えて下さい
aが比例定数だよ!
yはxに比例し、x=3のときy=−2分の5である。
x=6のときのyの値を求めなさい。
教えてください(泣)
>yはxに比例し、x=3のときy=−2分の5である。
x=6のときのyの値を求めなさい。
y=axに「x=3のときy=−2分の5」を代入して
aの値を求めてみよう
円柱の容器に一定の割合で水をいれた際、4cmの深さで7秒の場合の定数はどう求めたらいいですか?
>円柱の容器に一定の割合で水をいれた際、4cmの深さで7秒の場合の定数はどう求めたらいいですか?
1秒あたりに何cm入るかを求めてみよう。
そいつが比例定数だ
yはxに比例し、x=4のときy=3である。x=-12のときのyの値を求めなさい。
という問題がどうしてもわかりません。教えてください。
>yはxに比例し、x=4のときy=3である。x=-12のときのyの値を求めなさい。
「x=4のときy=3である」という情報から比例定数を計算しよう。
そしたら、その関数の式にx=-12を代入してyの値を出してみよう
比例の時の比例定数の求め方、すごくよくわかりました。
反比例の時の求め方はどうすれば良いですか?
>比例の時の比例定数の求め方、すごくよくわかりました。
反比例の時の求め方はどうすれば良いですか?
反比例の比例定数の求め方を読んでみて!
反比例の場合も?
>反比例の場合も?
反比例の比例定数の求め方を読んでみて
反比例が分かりません。教えてください。
反比例が分かりません。どういうやり方ですか?
>反比例が分かりません。教えてください。
反比例の比例定数の求め方を読んでみて
y−7がx+3に比例し、比例定数が4である。x=−5の時のyの値を求めなさい。←がわかりません。
>y−7がx+3に比例し、比例定数が4である。x=−5の時のyの値を求めなさい
比例の条件からy=axに数値を当てはめてみよう。
式が求まったらx=-5を代入してその時のyをゲットしよう
40このりんごを二袋に分けた、片方が8こ多い。この計算を教えて下さい。
>40このりんごを二袋に分けた、片方が8こ多い。この計算を教えて下さい。
多く分けた個数をxとしてみよう。あとは、少ない方をxで表して、
そいつらを足したら40になるっていう等式を作ればいいね
yはxの比例し、x=3のときy=2である。
x=5分の6のときのyの値を求めよ。←分かりません。
ご教授お願いします。
>yはxの比例し、x=3のときy=2である。
x=5分の6のときのyの値を求めよ。←分かりません。
ご教授お願いします。
「x=3のときy=2」という情報を使って比例定数を計算しよう。
あとはその比例の関数にx=5分の6を代入すればいいね
3点A(0,5),B(-1,a+3),C(3,1-a)が同じ直線上にあるとき、定数aの値を求めなさい。
この問題の解き方を教えて下さい。お願いします。
>3点A(0,5),B(-1,a+3),C(3,1-a)が同じ直線上にあるとき、定数aの値を求めなさい。
この問題の解き方を教えて下さい。お願いします。
Aは切片だからこの直線の式はy=Ax+5(傾きAは定数aと区別するために大文字)なはず。
あとはBとCの座標を代入してAとaを求めてみよう
比例定数が−5分の1である。
の解き方がわかりません。
教えてもらってもいいですか?
>比例定数が−5分の1である。
の解き方がわかりません。
比例定数はy=axのaのことね。
ってことは比例の式がわかるよね
次の(1)、(2)について、yをxの式で表して、yがxに比例することを示しなさい。
また、その比例定数を答えなさい。
(1) 縦が5cm、横がxcmの長方形の面積はycm2である。
ていう問題がわかりません!教えてください(T-T)
めっちゃ分かりやすいです!
明日テストなのに分からないところいっぱいあったのでこのサイトりようしましたw
分からないところ全部コンプリートしました!
絶対に満点取ります!
私ぃ、明日てすとなんですよぉ・・・
ちょう不安でぇ・・・
どぉしたら良いですかぁ?
てすとなんてやだぁ・・・
>次の(1)、(2)について、yをxの式で表して、yがxに比例することを示しなさい。
また、その比例定数を答えなさい。
(1) 縦が5cm、横がxcmの長方形の面積はycm2である。
長方形の面積の求め方を思い出そう。
(面積=縦かける横だったね?)
そしてその公式通りに縦、横、面積の値をぶちこんでyとxの式を作ろうぜ
反比例での比例定数の求め方を教えてください
yはxに比例しx=3のときy=15のときの比例定数を求めなさい。
どうやってやりますか??
答えはなんですか??