度数分布表??ヒストグラム??
こんにちは、レベニラ定食を愛してやまないKenです。
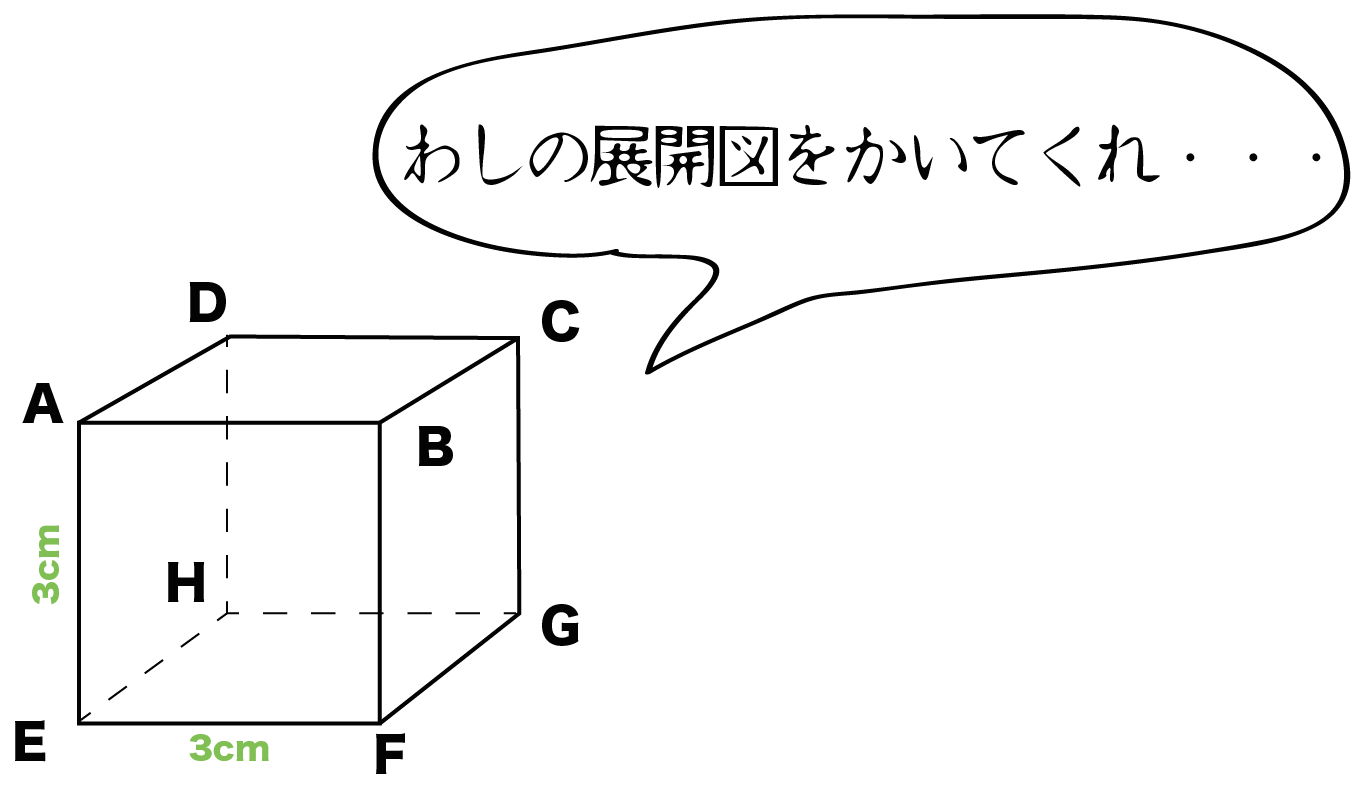
中学1年生の単元「資料の活用」で、
ヒストグラム
という数学用語が登場します。カタカナばっかでなんだか強そうですね笑? ただ、みかけによらずヒストグラムくんは案外たいしたことないんです。

今日はわかりやすい例といっしょに「ヒストグラム」について解説していきます!
~もくじ~
- ヒストグラムって何??
- ヒストグラムの書き方
ヒストグラムを一言でいうと・・・
ヒストグラムとはずばり、
「度数分布表」を棒グラフにしたもの
です。
えっ。度数分布表がよくわからないですって!?? そんな方は【資料の活用】度数分布表の「階級・度数」ってなに??という記事を参考にしてくださいね。
たとえば、度数分布表ってこんな感じのやつです。これはマメをつかむゲームの結果を度数分布表にしたものです笑

ヒストグラムではグラフの横軸に「階級」、縦軸に「度数」をとります ↓↓

どのようにヒストグラムを作ることができるんでしょうか?? 今日はヒストグラムの書き方を伝授します。
超わかりやすい「ヒストグラムの書き方」
ヒストグラムの書き方は以下の4つのステップですよ^^
Step1. ヒストグラムの「横軸」と「縦軸」をとる
ヒストグラムでは横軸に「階級」、縦軸に「度数」をとるんでしたね??
さきほど登場した度数分布表からヒストグラムをつくってみましょう。

すると、

こんな感じで縦軸と横軸がかけそうですね!
Step2. ヒストグラムに目盛りをふる!
ヒストグラムに縦軸と横軸の目盛りをふっていきましょう!
ヒストグラムの横軸は1つの「階級」ごとに目盛りをいれて、
縦軸は、「度数の最大値と最小値がおさまるよう」に目盛りをふりましょう!
さっきの例でいえば、
階級は「0~2」、「2~4」・・・というように2つずつ変化していますよね?? そのため、ヒストグラムの横軸の目盛りは2ずつとっていきます。こんな感じです↓↓

そんで、次は縦軸の「度数」ですね!
度数分布表をみると、度数の最小値は「0」、最大値は「4」です。0~4までの数字がおさまりそうな、0から5までの目盛りを縦軸にふってみます。

これでヒストグラムの目盛りは完ぺきですね!!^^
Step3. ヒストグラムに点をうつ!
次はヒストグラムに「度数」の値をいれていきましょう!
それぞれの階級の度数の点をうっていくだけでいいんです。さっきのヒストグラムは、

こうなりますね!
Step 4. 点を上辺とする長方形を書く
いよいよ最後のステップ。先ほどプロットした点が上の辺になるように長方形をかいていきます。

棒グラフをヒストグラムに書き込んだら必ず「点」を削除してくださいねー!

これでヒストグラムの完成です!書き方はぜんぜんむずかしくないですよね!?^^
ヒストグラムの書き方をゲットだぜ??
資料の活用で最初につまずく点が「ヒストグラム」。
これさえクリアできれば中学1年生の数学を攻略したも同然です!
次回は度数分布多角形について解説しまーす^^
それじゃねー!
Kenny
<<関連記事>>
- 中学数学で勉強する「代表値」とは??
- 中1数学の「資料の活用」を攻略する3つのコツ
- 【資料の活用】度数分布表の「階級・度数」ってなに??
- 【中学数学】3分でわかる!相対度数の求め方
- 【中学数学】3分でわかる!平均値の出し方
- 【中学数学】3分でわかる!「階級値」ってなに??
- 【中学数学】有効数字の1つの計算方法と考え方

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。
























質問する