ルート分数の足し算・引き算の練習問題をといてみよう!
こんにちは!この記事をかいてるKenだよ。耳鼻科がよんでるね。
勉強の仕上げに、つぎの練習問題をいっしょにといてみよう。
つぎの平方根の計算をしなさい。√3分の4 – √2分の1 + 6分の√2
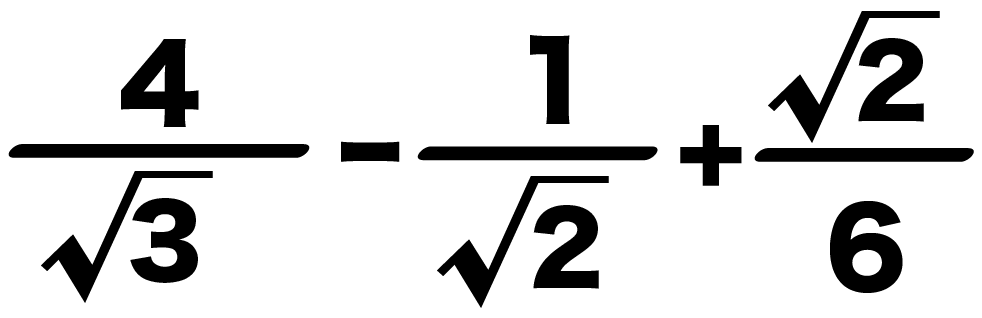
【解答】ルート分数の足し算・引き算の練習問題
この練習問題の解答は、
3分の(4√3 – √2)
だ。
計算方法を解説していくよ。
つぎの4ステップで平方根の分数の足し算・引き算ができちゃうね。
- 分母の有理化
- 通分
- 分子の足し算・引き算
- 約分
Step1. 分母の有理化する
まず分母の有理化だね。
分母を有理化してやると、のちのち通分がしやすくなるっていうメリットがあるんだ。
⇒ 分母の有理化のやり方はこちら
例題の計算では、
- √3分の4
- √2分の1
の2つの分数の分母に平方根(無理数)があるよね??
ってことは、こいつらで分母の有理化しなきゃいけないってことだ。

分母の平方根を分子と分母にそれぞれかけてやると、
- √3分の4 = 3分の4√3
- √2分の1 = 2分の√2
になるね!

Step2. 通分する
つぎは分数たちを通分しよう。
通分ってようは、
分母をぜんぶおなじ数にする
ってことだね。
分母の有理化みたいに、分母と分子におなじ数をかけてもいいから、
分母の数字をいっしょにしてみて。
例題の分数たちの分母は、
- 3
- 2
- 6
だね。
こいつらの最小公倍数は「6」。
だから、分母もぜんぶ6にそろえると、
3分の4√3 – 2分の√2 + 6分の√2
= 6分の8√3 – 6分の3√2 + 6分の√2
こうなるね!

Step3. 分子の足し算・引き算する
つぎは分子に注目して、
足し算・引き算をやっちゃおう。
平方根の足し算・引き算では、
√の中身がおなじ平方根どうしの係数を足し引きする
だったよね?
練習問題でもルートの中身がおなじ√2のこうどうしを計算してみよう。
すると、
6分の8√3 – 6分の3√2 + 6分の√2
= 6分の(8√3 -2√2)
になる。

Step4. 約分する
最後は分数の約分だ。
分母と分子におなじ約数があったら、そいつで分母と分子をわってあげればいいんだ。
例題では、分母と分子にはそれぞれ共通の、
2
っていう約数があるね。
こいつで分母と分子をわってやると、
6分の(8√3 -2√2)
= 3分の(4√3 -√2)
になるね!

これが答えだ。
どう??解けたかな?!