【平方根の計算】ルートの分数の足し算・引き算の仕方がわかる5ステップ

ルート（平方根）の分数の足し算・引き算の計算方法って！？？

こんにちは！この記事をかいてるKenだよ。どら焼きは脳にきくね。

ルートの計算には色々ある。

なかでも、いちばんむずいのは、

ルート（平方根）の分数の計算

だ。

ただでさえ、ルートの計算で精一杯。

なのに、そ、それを分数にしちゃうんだもん！？

クソやっかいだね。

今日は、ルート分数の計算をマスターするために、

平方根の分数の足し算・引き算の計算の仕方

を5ステップで解説していくよ。

ルートの分数の足し算・引き算の仕方5ステップ

さっそく計算方法を紹介していくよ。

5ステップで分数の足し算・引き算ができちゃうんだ。

1.  ルートを簡単にする
2. 分母の有理化
3. 通分する
4. 足し算・引き算
5. 約分する

例題をといてみよう。

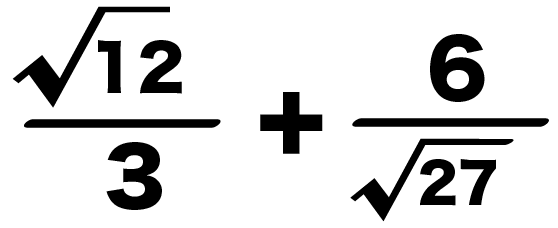
Step1. ルートを簡単にする

ルートを簡単にしよう。

ルートの中身から、2乗の因数をとりだせばいいのさ。

⇒　くわしくは「ルートを簡単にする方法」を読んでみてね。

例題の計算式では、

• √12
• √27

を簡単にできそう。

なぜなら、

ルートの中に2乗の因数がふくまれてるからね。

√12だったら、2の2乗、

√27だったら3の2乗が入ってる。

それぞれ簡単にすると、

3分の√12  + √27分の6
= 3分の2√3 + 3√3分の6

になるね。

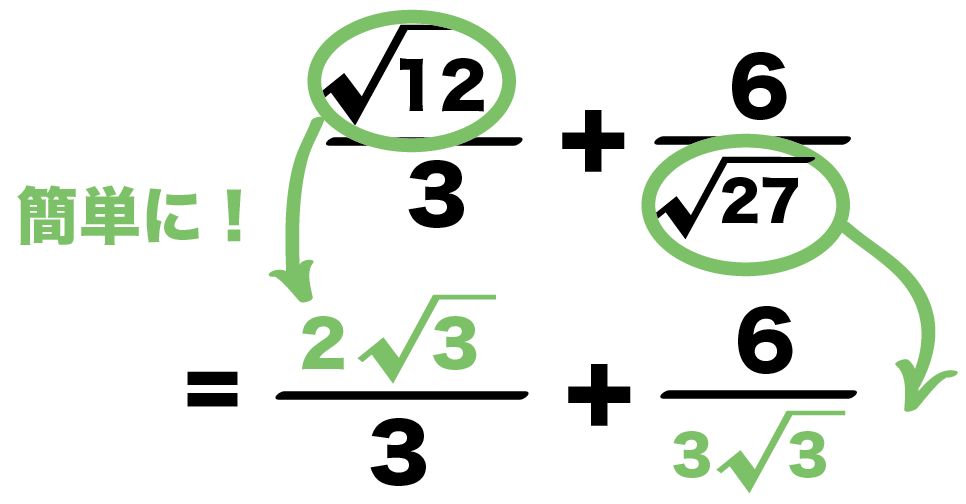
これが第1ステップ！

Step2. 分母を有理化する

つぎは、分母の有理化だ。

分母からルート（無理数）をなくせばいいんだ。

⇒　くわしくは「分母の有理化」をよんでみて^^

例題をみると、

2つめの項の分母に「√3」があるね。

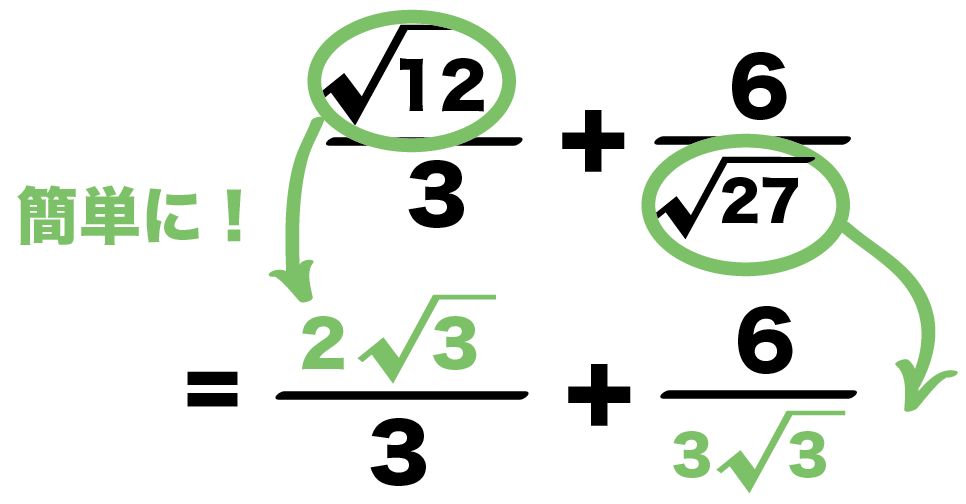
このルートをなくすために、

分母と分子に「√3」をかけるんだ。

すると、例題のルート計算式は、

3分の√12  + √27分の6
= 3分の2√3 + 3√3分の6
= 3分の2√3 + 9分の6√3

になる！

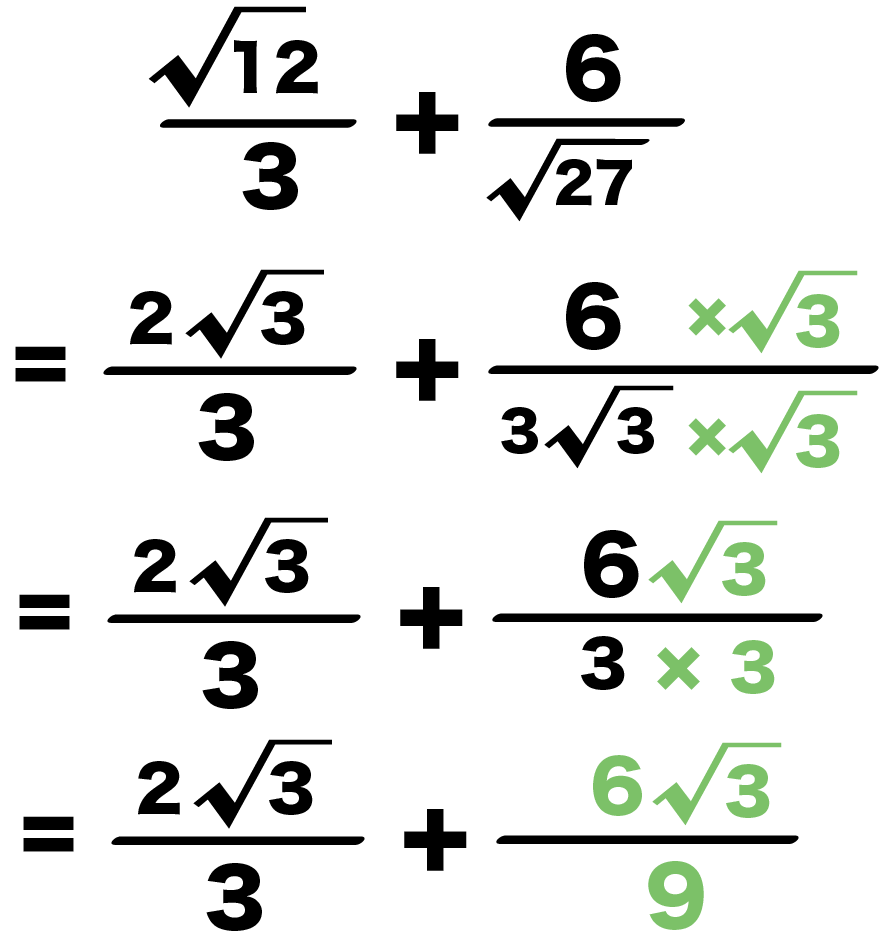
Step3. 通分する

つぎは、通分しよう。

通分ってようは、

分数たちの分母をそろえる

ってことさ。

例題の分数たちはそれぞれ、

• 3分の2√3
• 9分の6√3

だったよね？？

これじゃあ分母が「3」と「9」でバラバラだ。

分母を最小公倍数の9にあわしてやると、

• 3分の2√3 = 9分の6√3
• 9分の6√3

になるね！

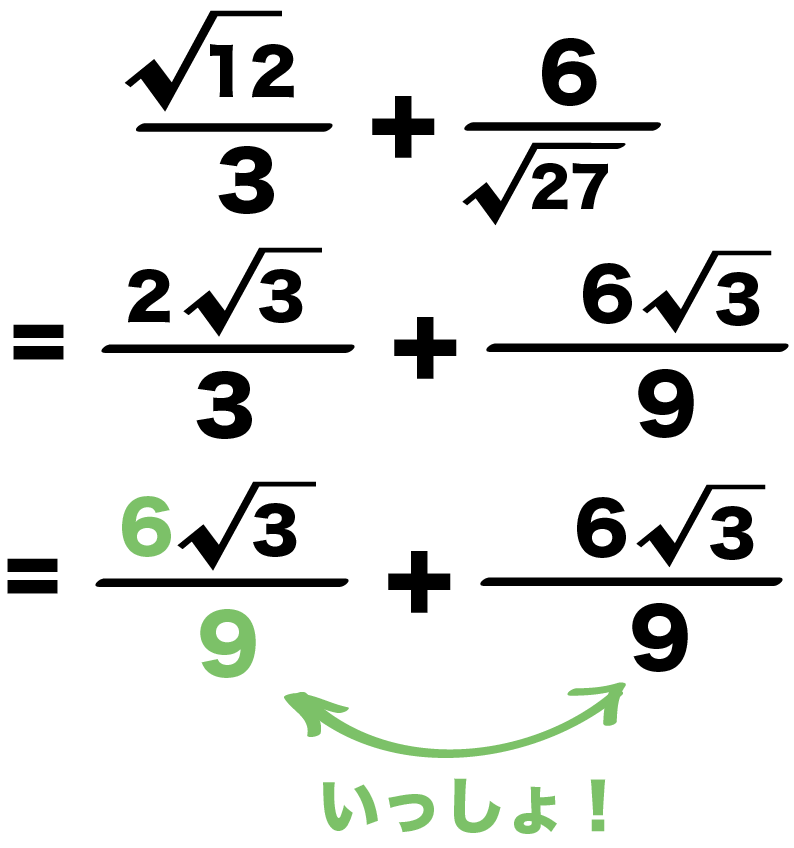
Step4. 足し算・引き算する

つぎは分子を足し算・引き算しちゃおう。

例題でも分子を足し算してやると、

3分の√12  + √27分の6
= 9分の6√3 + 9分の6√3
= 9分の12√3

になるね。

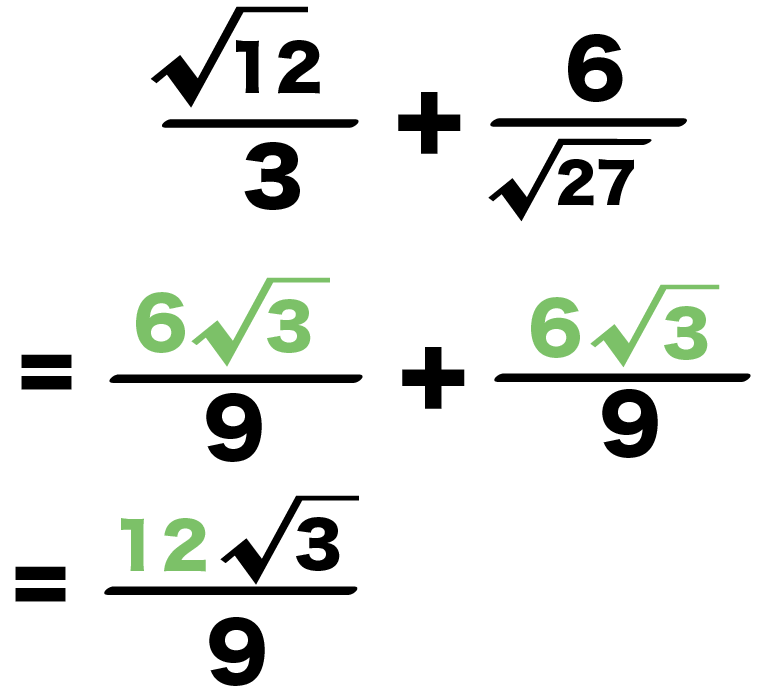
Step5. 約分する

最後は、ルートの分数を約分してみよう。

約分してすっきりしたほうがいいじゃん？

例題でも計算結果の、

9分の12√3

を約分しよう。

分母の「9」と分子の「12」の共通の約数に3がある。

ってことは、3で約分できるはずだから、

9分の12√3
= 3分の4√3

になるね。

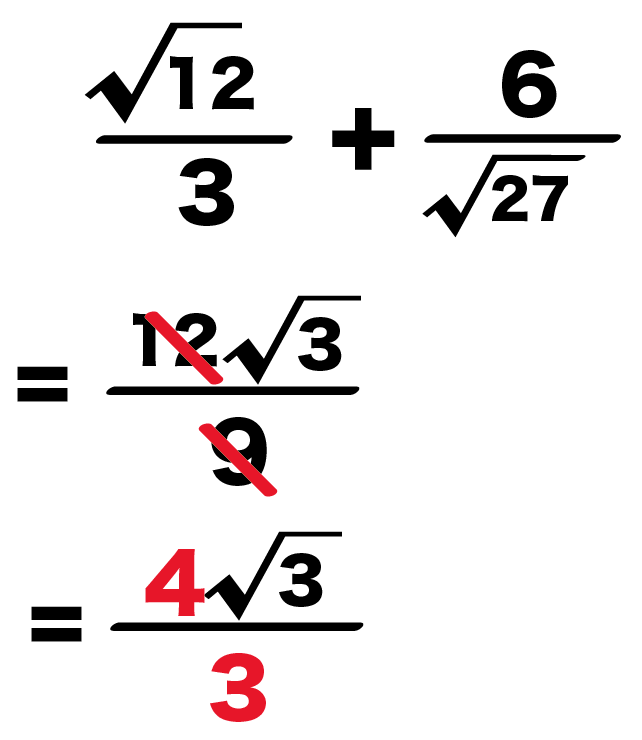
これでルートの分数の計算は終了だ！

まとめ：ルートの分数の計算は総合格闘技だ！

平方根の分数の足し算・引き算はどうだったかな？

5ステップもあってむずそうだけど、使っているのはどれも過去のワザ。

• ルートを簡単にする方法
• 分母の有理化
• 通分
• ルートの足し算・引き算

スムーズにとけるように踏ん張ってみよう。

練習問題

つぎの平方根の計算をしなさい。

√3分の4 – √2分の1 + 6分の√2

⇒練習問題の解答はこちら

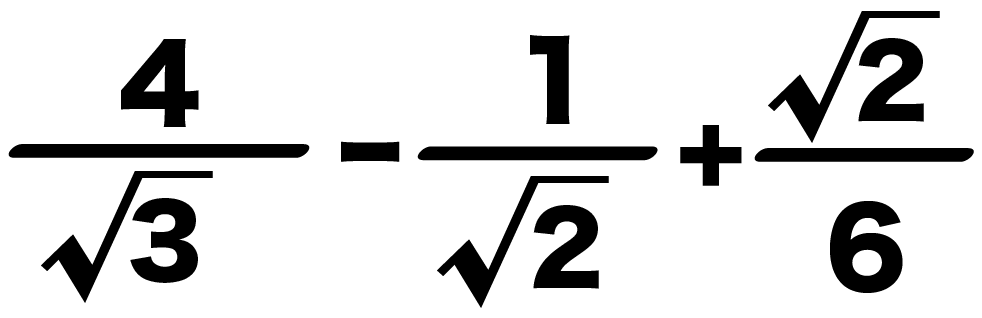
そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。