【長方形の性質】対角線の長さはなぜ等しいのか？？

長方形の対角線の長さってなんで等しい？？

こんにちは！この記事をかいているKenだよ。替え玉は必須だね。

長方形の性質の中に、

対角線の長さが等しい

ってやつがあるよ。

たとえば、長方形ABCDがあったとしよう。

このとき、

対角線AC = 対角線BD

になるってわけ。

対角線ACが12cmだとすると、

対角線BDも12cmになるんだ。

どう？？

むちゃくちゃ便利だよね？？

なぜ長方形の対角線の長さは等しくなるのか？？

でもさ、

なんで長方形の対角線の長さが等しいんだろう？？

不思議すぎるよね。

むしろ、怪しい。

そこで今日は、

なぜ長方形の対角線の長さが等しくなるのか？？

を4ステップで解説していくよ。

さっきの長方形ABCDをつかって証明していこう！

証明の方向性としては、

△ABCと△DCBの合同

を証明していくよ。

Step1. 長方形の定義をつかう！

長方形の定義は、

4つの角がすべて等しい四角形

だったよね？？

ってことは、

角ABC = 角DCB = 90°・・・（1）

だ。

Step2. 平行四辺形の性質をつかう！

長方形は平行四辺形の1種だったね？？

ってことは、

平行四辺形の性質がつかえるってわけ。

よって、

2組のむかいあう辺がそれぞれ等しい

より、

AB = DC ・・・（2）

になるね。

Step3. 三角形の合同条件をつかう！

BCは共通だから、

BC = CB ・・・（3）

(1), (2), (3)より、

2辺とその間の角がそれぞれ等しいから、

△ABC ≡ △DCB

になるね！

Step4. 合同な図形の性質をつかう！

合同な図形の性質をつかってあげよう。

対応する辺の長さはそれぞれ等しいから、

AC = DB

になるね。

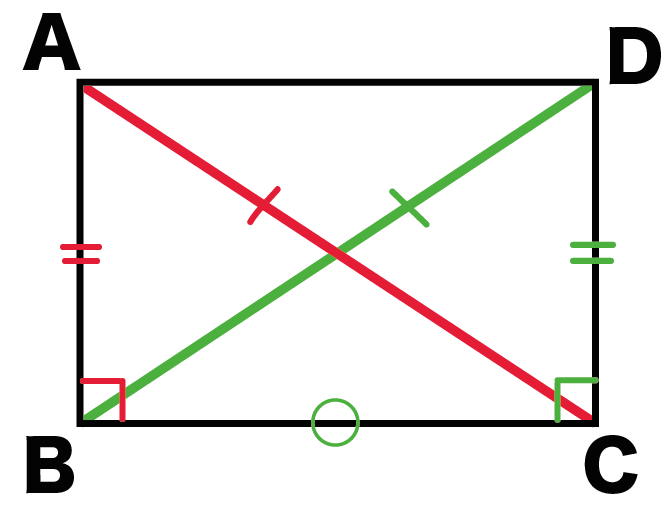
ACとDBは長方形ABCDの対角線だね？？

だから、

長方形の対角線同士が等しいっていえるんだ！

まとめ：長方形の対角線の長さはやっぱり等しい。

長方形の性質の、

対角線の長さはそれぞれ等しい

はおさえておこう！

三角形の合同で簡単に証明できるから安心だね。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。