【中学数学の応用】最高水準特進問題集をおすすめする3つの理由

難問・応用問題が満載！最高水準特進問題集

こんにちは！この記事をかいているKenだよ。コーヒーはインスタントでいいね。

数学で大切なのは「基礎」。

マイ勉でむちゃくちゃ勉強してきたね。

だけれども、

基礎がしっかりしていても入試で撃沈することがある。

なぜなら、

応用問題に慣れてないからさ。

基礎を理解したら応用問題をたくさんとく。

これが入試でいきてくるんだ。

今日は応用問題集としておすすめの、

最高水準特進問題集

を紹介するよ。

名前が長くて読みにくい？？

でもそんなの関係ないんだ。

最高水準特進問題集をおすすめする3つの理由

おすすめする理由は3つあるよ。

理由1. 学年別にチャレンジできるから

1つめのポイントは、

何年生でも入試問題に挑戦できる

とこだね。

入試問題は中学3年生がうけるもの。

だから入試問題って

中学3年生むけに作られたものばかりなんだ。

入試問題の中には、

• 中1の内容
• 中2の内容
• 中3の内容

がまじっていることになる。

中学1年生か過去問をとこうとしても、

あれ、これならったっけ？？

ってなっちゃう。

これじゃあ難問にチャレンジする気がうせるね。

だけど、「最高水準特進問題集」なら大丈夫。

なんと、

学年別×ジャンル別

で応用問題を出題してくれているんだ。

たとえば、

「中学1年生×空間図形」の入試問題

とかね。

問題集自体が「学年×教科別」でわかれているんだ。

中学数学1年、

中学数学2年、

中学数学3年、

みたいな感じで。

苦手な分野もピンポイントでチャレンジできるし、

憧れの入試問題もとくことができるね！

理由2. 解答がとりはずしできる

2つめの理由は、

解答冊子をとりはずせるから

さ。

えっ、どこがいいのかわからないって！？

そうだね。

問題集から解答冊子をとりだせると、

問題をみながら答え合わせ

が出来るんだ。

もし、問題集と解答冊子がいっしょになっていると、

問題文(39ページ)みて、

解答文(192ページ)みて、

問題文(39ページ)みて、

解答文(192ページ)みて、

問題文(39ページ)みて、

解答文(192ページ)みて、

・・・・・・

っていう手間が発生するはず。

だから、その手間がはぶけた「最高水準特進問題集」は便利ってわけ！

理由3. けっこうむずいから

なんといっても、

問題の質が高い。

つーか、

ムズい笑

たとえばつぎの問題がのってるよ。

※中1数学83ページから引用

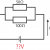
右の図のように、立体の各面の中央に、それぞれ通り抜けた同じ大きさの穴があいている。この立体の体積と表面積を求めなさい。ただし、穴の辺と立方体の辺は平行である。

こんな応用問題はまず教科書にはのってないw

立体の求め方は、

（立方体の体積） –  （穴があいてる体積）

で求められるはず。

よって、

（立方体の体積） –  （穴があいてる体積）
= ( 3×3×3 ) – (1×1×1 × 7)
= 20 [cm^3]

になるね。

でも表面積はもっとやっかい。

各面の面積(緑)と、

穴をあけてできた側面の面積（赤）

をたしてやるんだ。

よって、表面積は、

（各面の面積）＋（穴をぬいたときにできる側面積）
＝　{（3 × 3  -1 ）×6} + {1×1×4×6}
＝　48 + 24
＝　72 [cm^2]

になるね。

こんな感じで、

ひとひねりされた応用問題がたくさんのってるよ。

勇気だしてチャレンジしてみよう！

最高水準特進問題集（数学）には応用問題・難問だらけ

この問題集には、

息切れする応用問題ばかりだ。

基礎が固まったらチャレンジしていこう！

そんじゃねー

Ken

Ken

Qikeruの編集・執筆をしています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いでサイトを始めました。