5ステップでわかる！円錐が滑らずに転がる問題の解き方

円錐が転がる問題の解き方を教えてほしい！

この記事を書いているKenだよ。下痢に、勝ったね。

中学数学ででてくる円錐の問題には

• 円錐の表面積の求め方
• 円錐の側面積の求め方
• 円錐の体積の求め方
• 円錐の高さを求める問題
• 円錐のひもの問題

とかいろいろあるけど、もう1つでてきやすいのが

円錐を転がす問題

だね。

例えば次のような問題↓

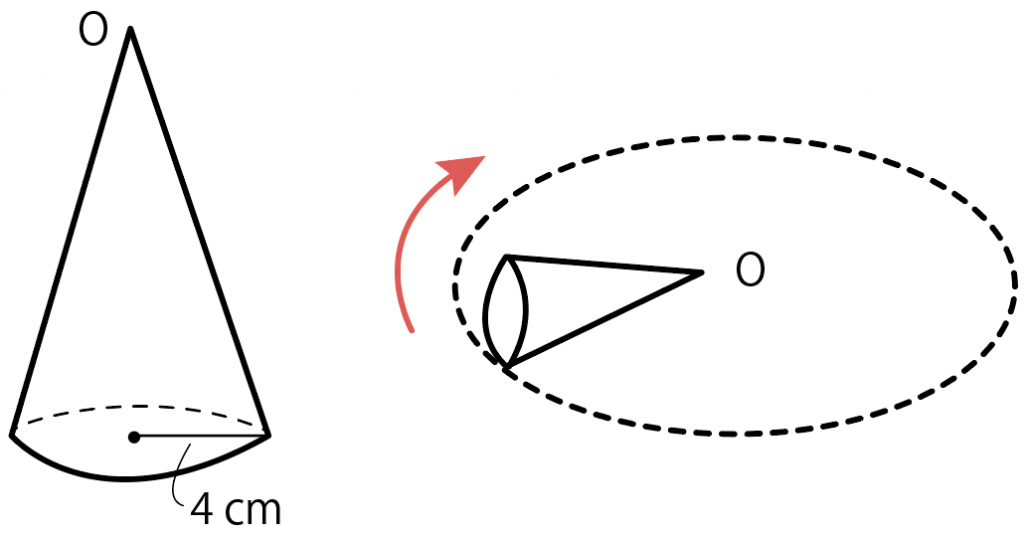
わざわざ円錐を転がすぐらいだから難しそうだけど、ゆっくり解いていけば大丈夫。

Step1. 円錐の転がった距離を求める

まずは円錐の転がった距離を求めてみよう。

図でいうと、この円の円周の長さだね↓

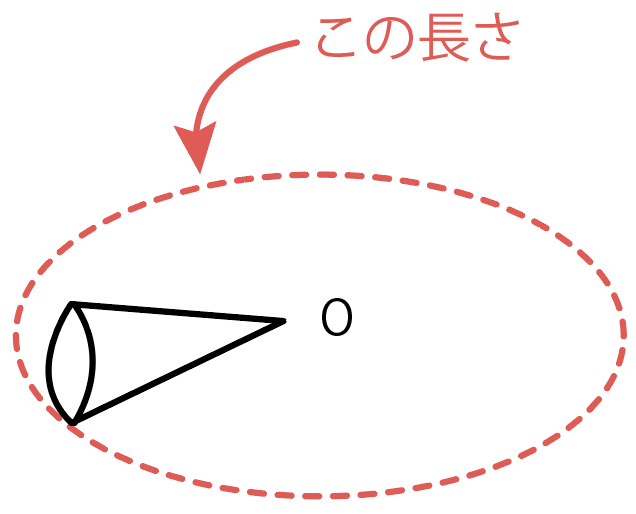
円錐が転がらずに回ったとすれば、円錐の底面のふちが移動した距離は、

回転数 × 底面の円周の長さ

で求められるよ。

この問題だと、

• 回転数 = 4
• 底面の円周長さ = 半径4 cm × 2× 円周率π = 8π

だから、

になるね。

Step2. 母線の長さを求める

次は母線の長さを求めよう。

母線とは、「円錐の頂点から底面への長さ」のことだね。

この母線を求めるためには

母線が作る円の円周長さ = 円錐のふちが動いた距離

という方程式を作ればいいよ。

母線をrとしてやると、

となって、母線の長さは16 cm になるはずだ。

Step3. 展開図をかいてみる

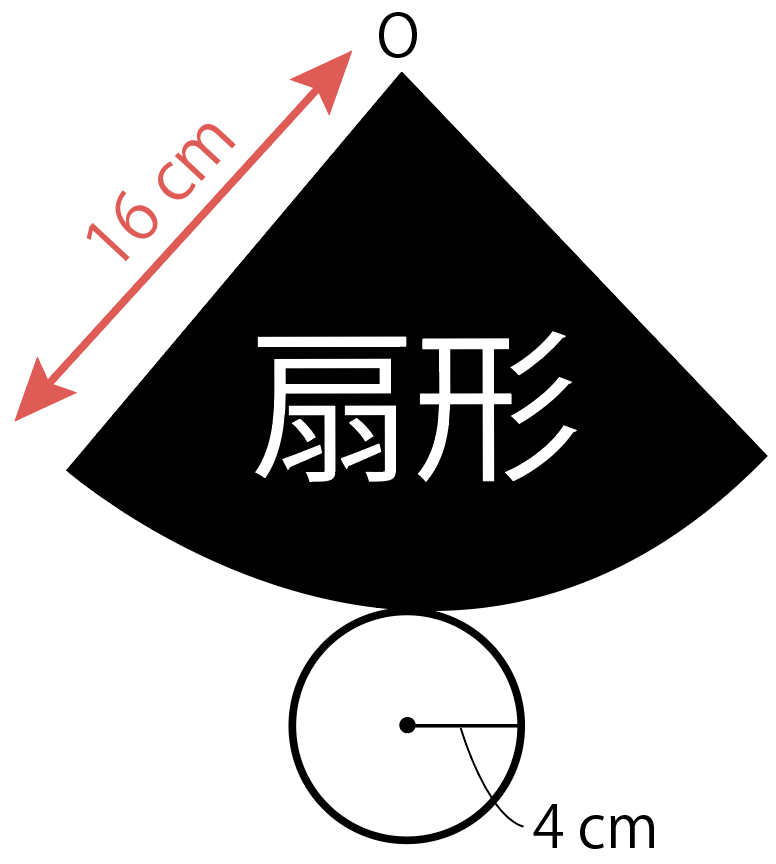
母線が16 cm とわかったから、問題の円錐はこんな感じになってるね↓

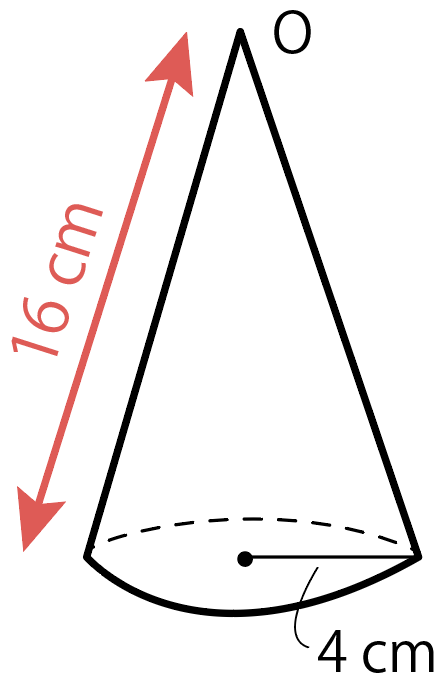
ここで冷静になって、側面積を求める前に円錐の展開図をかいてみよう。

Qikeru：学びを楽しくわかりやすく

 

1 Pocket

2015.03.22

【簡単作図】円錐の展開図の書き方がわかる4つのステップ

https://media.qikeru.me/corn-development

円錐の展開図の書き方・作図方法がわからない！！こんにちは、この記事をかいているKenだよー。緑ペンがほしいね。 円錐の表面積を求めなさいっ！っていう問題はけっこうでる。先生はだしたくなる。だけど、円錐の表面積を求めるのはけっこうムズい。できれば避けて通りたいね・・・・このピンチを助けてくれるのが、円錐の展開図を作図するということなんだ。円錐を切り取ったら円錐はどんな紙切れになるのか？？円錐の展開図の書き方を知っていると、いとも簡単に表面積まで計算できちゃうんだ。今日は、その、円錐の展開図の書...

円錐の展開図は

• 側面の扇形
• 底面の円

でできているよね？

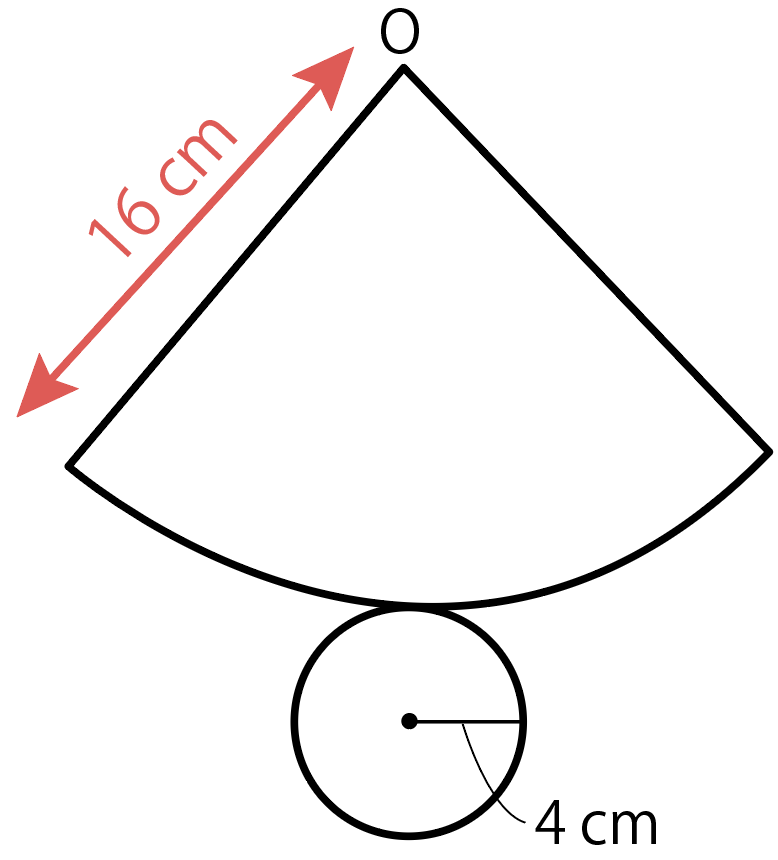
つまり、円錐の側面積は「扇形」になるわけだ。

扇形の面積の求め方は、

半径×半径×中心角÷360

で求められる。

Qikeru：学びを楽しくわかりやすく

 

6 Pockets

2015.03.16

【中学数学】3分で簡単にわかる！「扇形（おうぎ形）の面積の求め方」の公式

https://media.qikeru.me/area-of-fan

扇（おうぎ）形の面積の求め方の公式を簡単に覚えたい！こんにちは、この記事をかいているKenだよー。コーヒーは何度飲んでもうまいね。 「円とおうぎ形」という単元では、 円 おうぎ形（扇形）という2つの図形について勉強していくよ。  前回まで、 円の面積の公式 円周の長さの求め方っていう2つの公式をマスターしてきたね。今日は、「扇形の面積」について詳しく勉強していこう。「面積の求め方の公式」をおぼえていればテストでも楽勝さ。 ~もくじ~ 扇形の面積の求め方の公式 なぜ公式がつかえるのか？...

だから、面積を求めるためには「扇形の中心角」が必要になってくるんだね。

Step4. 側面の扇形の中心角を求める

側面の扇形の中心角を X として方程式を作ってみよう。

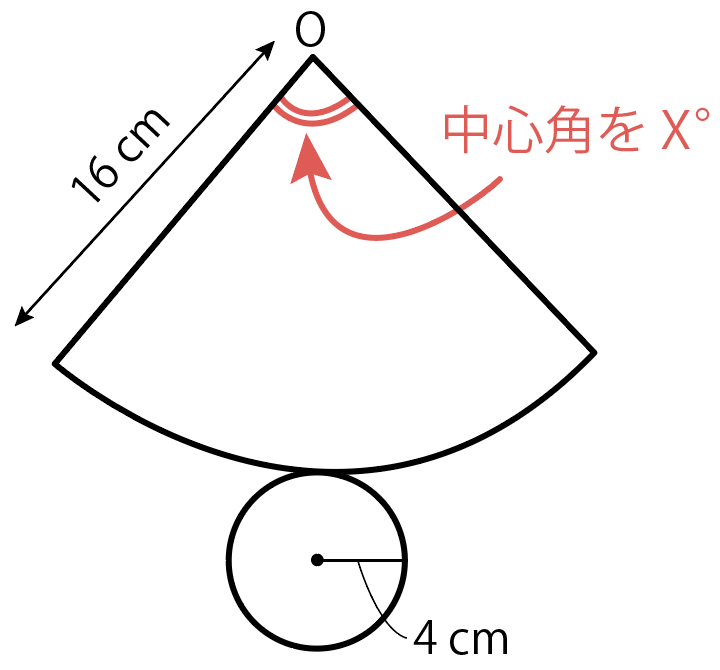
扇形の弧の長さ = 底面の円周の長さ

という方程式を作って、中心角を求めればいいね。

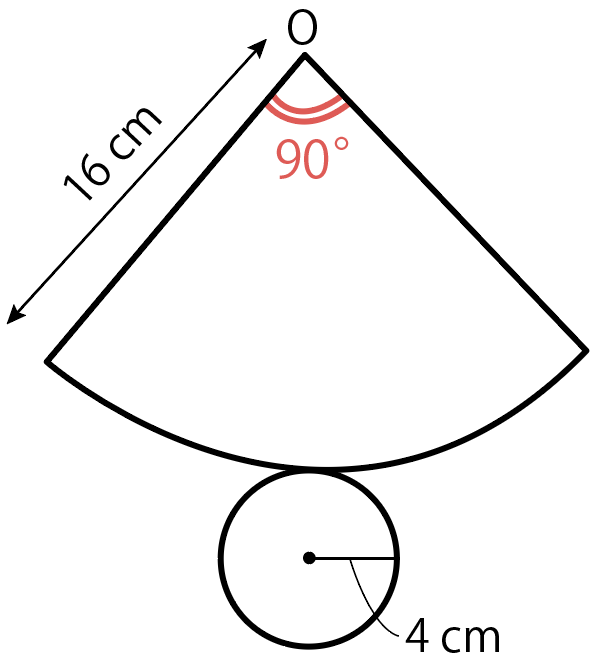
例題では、

16× 2π × X ÷ 360 = 8π

という式ができて、

X =90°

になるはず。

「扇形の中心角の求め方」がいまいちわからない時はこの記事で復習してみてね↓

Qikeru：学びを楽しくわかりやすく

 

4 Pockets

2015.03.18

【カンタン公式】扇形の中心角の求め方がわかる3つのステップ

https://media.qikeru.me/fan-central-angle

 扇形の中心角の求め方の公式を知りたい！こんにちは、この記事をかいているKenだよー！豆乳ラテだったら3杯はいけるね。 「扇形の中心角の求め方」の公式ってチョー便利。教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。たとえば、半径 4 、弧の長さが 6π の扇形があったとしよう。この「扇形の中心角」を求めたいときは公式をつかえ...

Step5. 側面積を求める

いよいよ扇形の面積の公式を使って、側面積を求めていこう。

扇形の面積の公式は

半径×半径×円周率×中心角÷360

で求められるから、

が正解だね。

円錐が転がっても動ずるな！

こんな感じで、円錐が転がっちゃう応用問題もステップを踏んでやれば大丈夫。

転がる問題を解くために必要なのは、

• 円錐の展開図の書き方
• 扇型の中心角の求め方
• 扇型の面積の求め方

の3つだけ。

ひるまずにチャレンジしてみてね。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。