食塩水の文章問題で混ぜてきたらどうする?
食塩水の問題は、食塩水ってだけで厄介だけど、たまに、
混ぜる系の文章問題
が出てくるんだ。
例えばこんな感じ↓
この文章題の特徴は、
混ぜている
ってこと。
食塩水をちょっと取り出して、代わりに水を混ぜちゃってる。
いかにも難しそうだけど、冷静になって次の4ステップを踏めば解けるよ。
とりあえず、図をかく
まずは、ゆっくりと、
問題内容を図で整理してみよう。
さっきの例題では、
12%の食塩水600gからxg取り出し、取り出した分だけ水を加えて、その結果600g7.2%の食塩水になったんだね?
この様子を図にあらわすとこんな感じだ↓
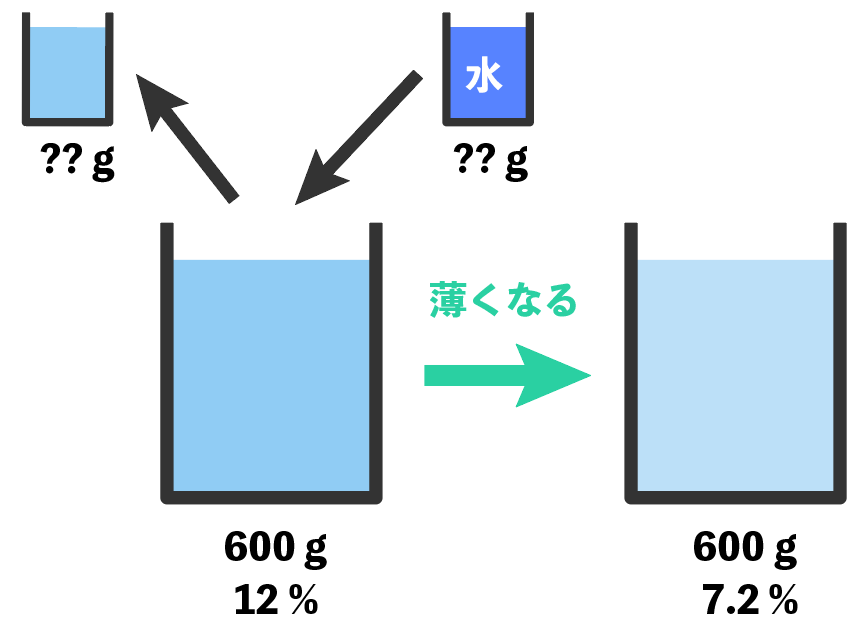
図を描くときのポイントは、
- 食塩水の重さ
- 濃度
を食塩水の下にメモすることだよ。
問題でわかっている情報を整理してみよう。
「求めたいもの」をxとおく
食塩水を混ぜようが捨てようが、方程式の文章問題の鉄則は変わらない。
それは、
「求めたいもの」を文字でおく
だ。
例題だと、
くみ出した食塩水の量(重さ)
を求めたいから、こいつを「x g」と置いてやろう。
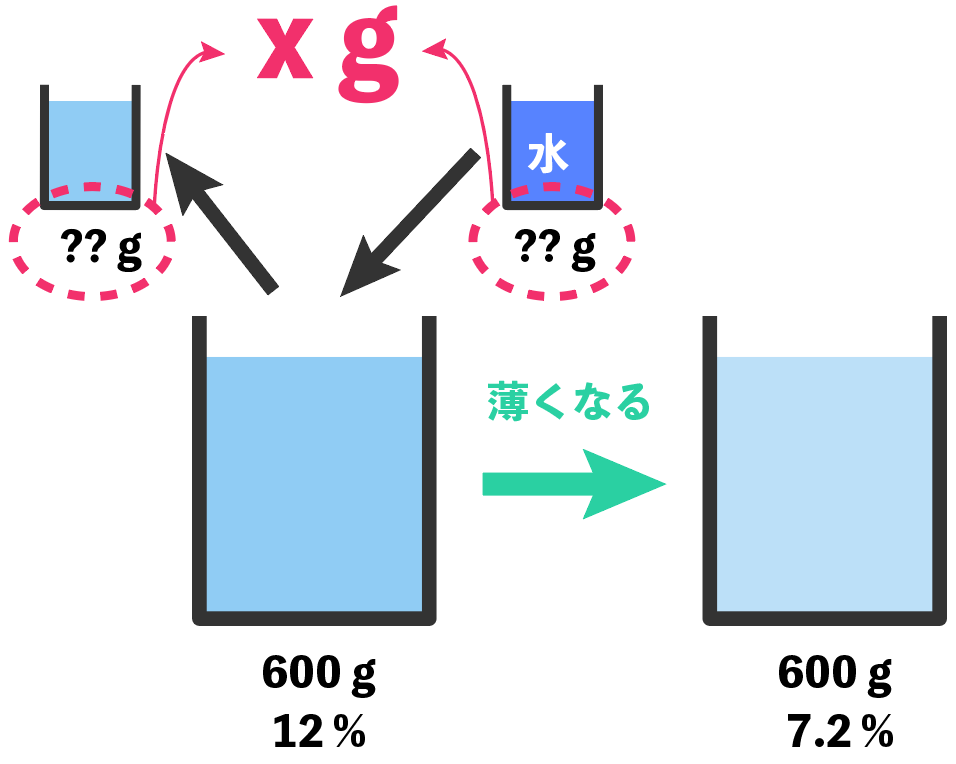
「食塩の重さ」で等式を作る
食塩水をかき混ぜようが、塩を新たに加えようが、シェイクしようが、
食塩水の文章題では「食塩の重さ」で等式を作る
のが鉄則。
例題だと、
(くみだす前の食塩の重さ) – (くみ出した食塩の重さ)=(残った食塩の重さ)
という等式を作ってあげればいいね。
具体的にいうと、
(600 g 12%の食塩水に入ってる食塩の重さ)-(x g 12%の食塩水に入ってる食塩の重さ)= (600g 7.2% 食塩水に含まれる食塩の重さ)
になる。

ここで思い出したいのが食塩水の公式。
食塩水の重さは、
(食塩の重さ)=(食塩水の重さ)× (濃度)
で求められたよね。
方程式を解く
公式を使って式を立てると、
600×100分の12 – x ×100分の12 = 600×100分の7.2
になる。
この方程式はなんという偶然か「分数を含む方程式」。
分数が含まれている場合、分母の最小公倍数を両辺にかけるのが常套手段だったね。
分母の最小公倍数「100」を両辺にかけると、
600×100分の12 – x ×100分の12 = 600×100分の7.2
12(600-x) = 600 × 7.2
x = 240
となる。
xはくみ出した食塩水の重さだったから、答えは「240 g」だ。
という感じで、混ぜる系の食塩水も冷静になればノープロブレム。
諦めずにチャレンジしてみてね。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。








『5%の食塩水200gと14%の食塩水300gがある。いま、それぞれから同じ重さの食塩水を取り出した
残りを混ぜて11%の食塩水を作りたい。5%、11%の食塩水を何gずつ取り出せばいいか求めよ』
という問題が全く分かりません。教えてください!
食塩水Aと食塩水Bを10gずつ取り、両方を混ぜ合わせた。このときにできた食塩水の質量パーセント濃度は何%か。
ちなみに、食塩水Aは食塩10gを水に溶かして質量パーセントを10%にした。
食塩水Bは食塩20gを水に溶かして質量パーセントを20%にした。
教えてください!
お願いしていいですか?
10%の食塩水が340gある。この食塩水に食塩を加えて15%の食塩水を作るには食塩を何g加えればいいか答えなさい。
という問の15%にした時の食塩と食塩水の求め方がわかりません
教えていただけると嬉しいです。
すごつつ