円錐にかけたひもの最短距離を求める3ステップ

円錐にかけたひもの最短距離を知りたい？？

こんにちは！この記事をかいているKenだよ。バターチキン最高。

円錐にひもをかける問題ってあるよね？？？

たとえば、つぎのような問題だ。

例題

母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。

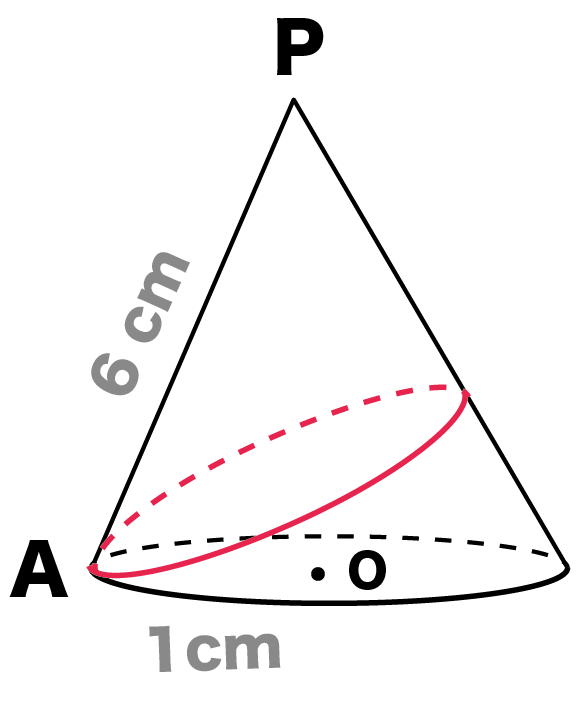
なんで円錐にひも？？？

って思うかもしれないね。

正直、とくのがつらい。

だけど、

円錐にかけたひもの最短距離を求める問題

ってよくでてくるんだ。

今日はこのタイプの問題の、

円錐にかけたひもの最短距離を求める問題の解き方

を3ステップで解説してみたよ。

よかったら参考にしてみてね。

円錐にかけたひもの最短距離を求める3ステップ

3ステップでとけちゃうよ。

1. 展開図をかく
2. 中心角をだす
3. 直角三角形の比をつかう

例題をといていこう。

例題

母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。

Step1. 展開図をかく

円錐の展開図をかいてみよう。

とりあえず、円錐の展開図っぽいやつをかこう。

中心角は気にしなくていいよ。

これが第1ステップさ。

Step2. 側面の中心角をだす

つぎは側面の「扇形の中心角」をだしてみよう。

出し方は簡単。

中心角をxとして方程式をたてればいいんだ。

側面の扇形の弧の長さ

と

底面の円周の長さ

が等しい

っていう式をつくればOK。

例題をみてみよう。

中心角をxとしたから、

• 扇形の弧の長さ：　2×6 ×π× X ÷ 360
• 底面の円周長さ：　2× 1 × π

になるね。

だから方程式は、

（扇形の弧の長さ）＝（底面の円周長さ）
2×6 ×π× X ÷ 360　＝　2× 1 × π

になる。

これをといてやると、

中心角X　＝　60°

になるはずだ。

Step3. ひもをかく

つぎは展開図に「ひも」をかいてみよう。

例題でいうと、赤いひもは、

AからスタートしてAにもどってきているよね？？

しかも、その長さが最短距離。

ってことは、展開図でいうと、

A

と

組み立てたらAに重なるA’

を直線でむすんでやればいいんだ。

Step4. 直角三角形の比をつかう

最後は直角三角形の比をつかおう。

「ひも」と「母線」でできた三角形に注目してくれ。

例題でいうと、△PAA’だね。

こいつは、

• 頂角P = 60°
• PA = PA’ = 6 cm

の二等辺三角形。

二等辺三角形の性質の、

頂角の二等分線は底辺を垂直に二等分する

というやつを使ってみよう。

PからAA’に二等分線をひく。

交点をHとすると、

• 角AHP = 90°
• 角APH = 30°

になるね。

んで、

△APHは頂角30°の直角三角形だから、

1 : 2: √3

の辺の比になっているはず。

よって、

AP： AH = 2: 1
AH = 3 cm

になる。

PHはAA’の垂直二等分線になっているはず。

よって、

ひもの長さAA’
=  2 × AH = 6 cm

になるね。

おめでとう！

これで、ひもでも糸でもなんでもこいだね！

まとめ：円錐にかけたひもの最短距離は超総合問題！

最短距離の問題って、

• 扇形の中心角の求め方
• 円錐の展開図の作図
• 直角三角形の比

の知識が必要になってくる。

ってことはつまり、

1~3年生の知識をフル活用しないと解けない。

だから入試問題にでやすいのかもね。

テスト前によーく復習しておこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。