【いろいろな因数分解】置き換え問題の解き方がわかる3ステップ

因数分解の置き換え問題の解き方を知りたい！？

こんにちは！この記事をかいているKenだよ。爪は大事だね。

因数分解の応用問題の1つに、

置き換え問題

ってやつがいる。

世界には数えきれないほど因数分解の問題があるから、

ぜんぜんピンときてないかもね。

置き換え問題はつぎのようなやつだよ↓↓

こんなかんじで、

式のなかに「おなじ文字式」がちらほらしている問題。

えっ、この問題でいうと、

（2x+3）

がちらほらしてるじゃん？？

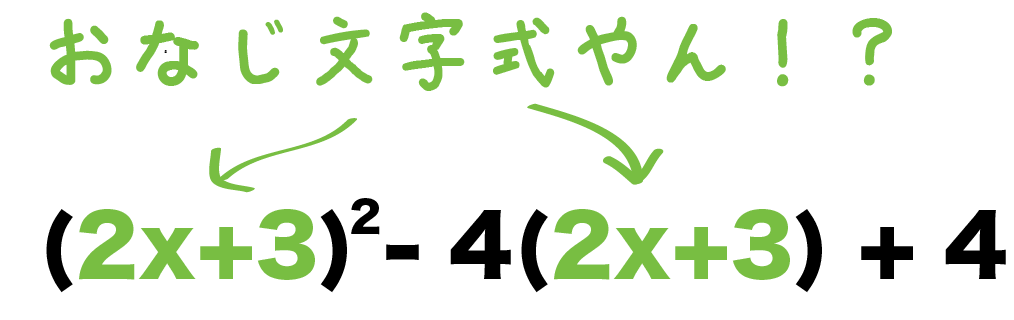
このタイプの解き方は一択。

チラホラしている文字式を「別の文字」で置き換えればいいんだ。

むちゃ解きやすくなる。

だから、

置き換えタイプの因数分解

とよんでるよ。

今日はこいつの解き方を5ステップで解説していくね。

因数分解の置き換え問題がわかる4ステップ

置き換え問題は4ステップでとけちゃうよ。

1. おなじ文字式をみつける
2. 文字式をAとおく
3. 因数分解する
4. Aに文字式を代入する

それじゃあ、さっきの例題をといていこう。

Step1. おなじ文字式をみつける

まず、式の中にふくまれている、

2回以上登場する文字式

をみつけてみよう！

これが探せないと始まらないね。

例題をみてみると、あきらかに、

2x+3

が何回もでてきてるよね？？

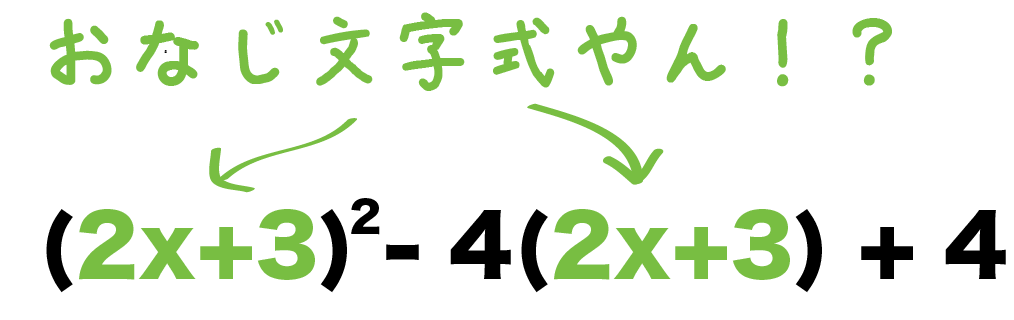
まあ、、2回だけどねw

こいつみたいに、怪しい文字式をみつけてみよう！

Step2. 何回もでてきた文字式をAとおく

つぎは、2回以上でてきた文字式を「A」とおこう。

そう、

アルファベットのAだ。

他の文字と区別するために大文字にしてね^^

すると、例題ではこんな感じで置き換えられるよ↓↓

A² – 4A + 4

これが第2ステップ。

Step3. Aについて因数分解する

つぎはふつーに因数分解してみよう。

置き換えた式を因数分解の解き方で計算すればいいのさ。

例題の式は、

A² – 4A + 4

に生まれ変わったよね？？

こいつを公式で因数分解してやろう。

因数分解したい文字式の項を数えてみると、

「3つ」あるね。

3つの項を因数分解する公式は、

(x+a)(x+b) = x² +(a+b) +ab

だったよね？？

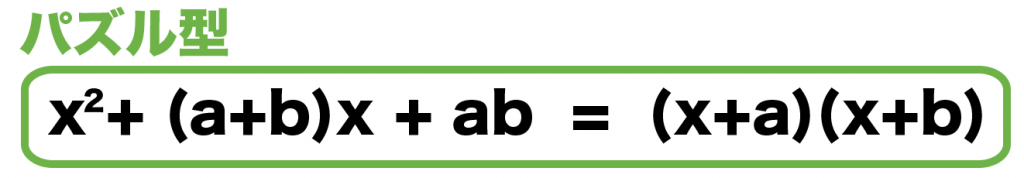
これはパズル型の公式。

かけて右に、たして真ん中になる数の組み合わせを考えればいいんだ。

例題の、

A² – 4A + 4

でいうと、

• かけて4
• たして-4

になる組み合わせを考えればいいんだ。

まず、かけて「4」になる組み合わせは、

• 2×2
• (-2)×(-2)
• 1×4
• -1×(-4)

の4通りだ。

このうち、たしたら「-4」になるのは2番目の、

• -2
• -2

だね。

こいつらを公式のaとbに代入してやると、

A² – 4A + 4
= (A-2)(A-2)
= (A-2)²

になるね。

Step4. Aに代入しなおす

最後はAに文字式を代入しなおそう。

つまり、

Aをもとの文字式にもどすってことだね。

例題では、

A = 2x + 3

っておいてたよね？？

こいつをさっき因数分解した、

(A-2)²

に代入してみよう。

さっそく代入してみると、

(A-2)²
= (2x +3 -2)²
= (2x +1)²

になるね！

おめでとう！

これで置き換えの因数分解もマスターだ^^

まとめ：置き換えの因数分解は置き換えて代入しなおす

因数分解の置き換えの問題？？

びびることはない。

おなじ文字式をいったんAとおいて、因数分解する。

最後にAをもとにもどせばいいんだ。

ガンガン置き換えていこう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。