二次関数の変域を求める問題って??
ある日、数学が苦手なかなちゃんは、
二次関数の変域の問題に出会いました。

関数y=x²について、xの変域が -2≦x≦4 のとき、yの変域を求めなさい。

二次関数の変域・・・・?
変域って、
聞いたことあるな。。
でてきたもんね。
でも、
今回は2次関数。。
なんか違う気が・・・
おっ、
いいところに気づいた!
二次関数の変域のナゾ
を解き明かしていこう!
一次関数と二次関数の変域の違うところ?
一次関数の変域って覚えてる?
わ、わすれた!!
二次関数の変域は違うの?
そう!
yの最大・最小値が
xの変域の端にならないことがある!!
へっ!?
なんで??
それは、
グラフの形に秘密がある。
たとえば、
この二次関数のグラフ
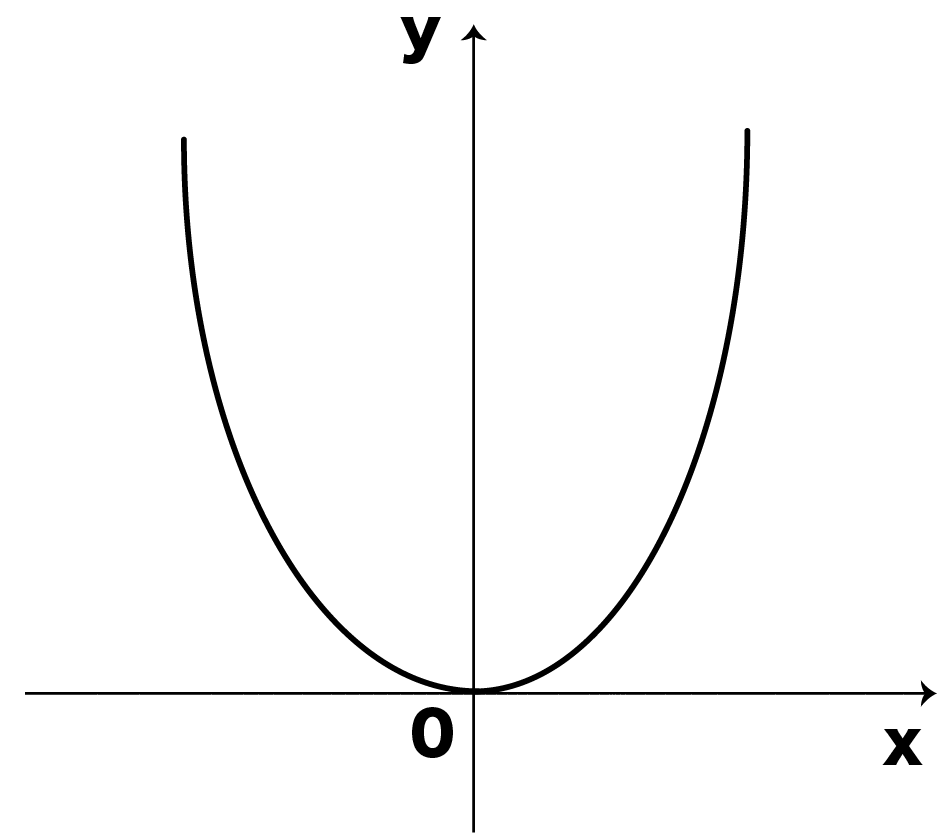
y軸に左右対称だ!
1次関数のグラフとの違い
分かったかな?
はい!
このグラフだと、
yが0より小さくなること
はないですよね!

そう!
じゃあ、
比例定数の正負が
グラフにどう影響あたえる??
一次関数だと、
比例定数の正負によって、
右上がり、
右下がりだった!

うん。
じゃあ、二次関数はというと、
↓を見比べてみて!!

yの変域が特殊。
0で一番小さいときと、
0が一番大きいときがある!!
よく気が付いた!
二次関数の変域の問題の求め方3つのコツ
こっから本番!
練習問題をといてみよう。
関数y=x²について、xの変域が -2≦x≦4 のときのyの変域を求めなさい。

コツ1. 「比例定数aの正負の確認」
y=x²
の定数aは正負どっち?
aは1!
ってことは、
「正」だ!

そう!
簡単でも確認は大事
コツ2. 「xの変域に0が入るか
xの変域に、
0が入るかどうか
を確認すること。
これ、大事!!
なんでかって、グラフを見て!
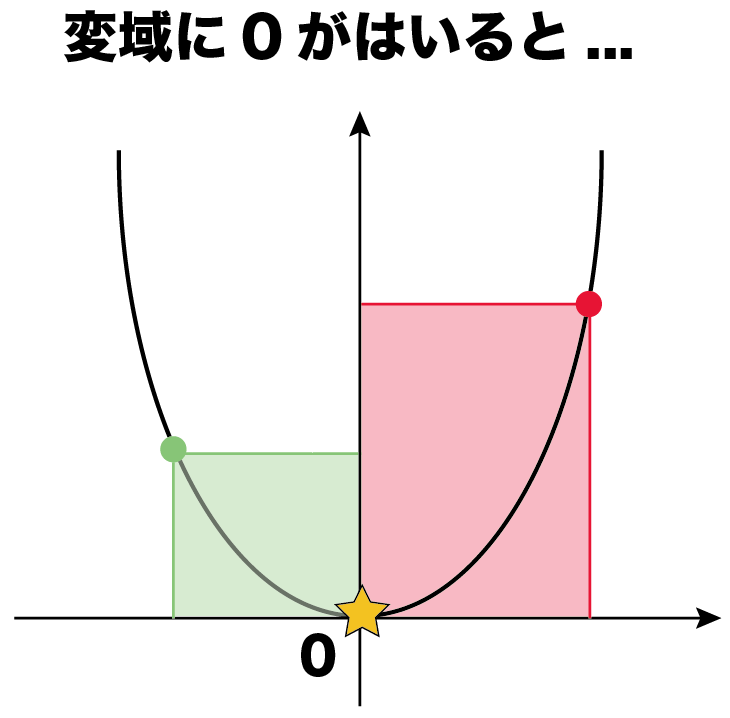

xの変域に0が入るとやばい。
yの変域の最小が0になる!
そう!
さっきの問題の変域、
「-2≦x≦4」
には0はいってる??
入ってる!
コツ3. 絶対値が大きいXを代入
絶対値が大きいほう
だよ。
念のため確認。
-2と4、
絶対値が大きいのは?
どっちだっけ・・・・・・
絶対値は、
正負関係なく、数字が大きいほど大きい
よ!
ってことは、
4だ!
xの変域に0がふくまれるときは、
絶対値が大きいxを代入する
って覚えよう!
はい!!
さっそく代入してみます。
絶対値が大きいxは4。
y=x²に代入すると、
4×4=16になる。
yの変域は、
0≦y≦16かな!
二次関数の変域とけてるじゃん!
やっっったーあーーー!
まとめ:二次関数の変域の問題はグラフをかくのが一番楽!
二次関数の変域のポイントは、
グラフをかくこと。
これにつきるね。
グラフだと
わかりやすかった!!
でしょ??
ここまでをまとめるよ。
【定数aの正負】→【xの変域に0が入るか】→【代入は絶対値が大きいほう】
変域が求められるといいね!
が、がんばります!
練習問題つくったよ!
解いてみよう!
【1】y=2x²において、
- -2≦x≦4のときのyの変域
- 1≦x≦5のときのyの変域
【2】y=-x²で、
- -3≦x≦6のときのyの変域
- -3≦x≦-1のときのyの変域
ありがとうございます!

年齢不詳の先生。教育大学を卒業してボランティアで教えることがしばしば。






最後の練習問題の解答はどこにありますか?
【1】
【2】
関数y=x2乗において、xの変域が―3≦x≦1の時、yの変域を求めよの式を教えてください。
二次関数の変域の問題はグラフを書いて方がいいね!
とくに、xの変域が0をまたぐ問題は要注意
上昇温度、発熱量の求め方
関数y=1/2×2乗のxの変域がa−5≦x≦aのとき、yの変域が0≦y≦8となるような定数aは、どうやったら求められますか?
>関数y=1/2×2乗のxの変域がa−5≦x≦aのとき、yの変域が0≦y≦8となるような定数a
ポイントはこの関数のaが正の数であって、
なおかつyの最小値が0になってることだね。
ってことは、xの変域が0をまたいでいるはずだから、
aは正の数、a-5は負の数であるはずだ。
鉄道の問題
>鉄道の問題
鉄道の問題は図をかくとわかりやすいよ。
列車の長さが道のりに与える影響がわかりやくなるよ
y=ax²+bx-3がx=2で最大値1をとるとき、a,bの値を求めよってどうすればいいですか??
>y=ax²+bx-3がx=2で最大値1をとるとき、a,bの値を求めよってどうすればいいですか??
x=2で最大値1を取るってことは、
y=(x-2)2 +1 になるはずだね。これを展開してaとbに当てはまる係数を答えよう
変域に0が入ってるか入ってないかはどうやって分かるんですか?
>変域に0が入ってるか入ってないかはどうやって分かるんですか?
変域の端と端の符号が違うと、0が入ってることになるよ。
例えば、-1
-2<X≦3は0≦y≦18ですが、なぜ-2の所 は<なのに0の所は≦になってるんですか?全く分かりません
>-2<X≦3は0≦y≦18ですが、なぜ-2の所 は<なのに0の所は≦になってるんですか?全く分かりません
=がつかないと、不等号の端っこは範囲に含まないってことになるよ。
詳しくは「不等号の意味」を読んでみてね
y=-4x2乗について、xの変域が-5≦x≦1のとき、yの変域を求めなさい という問題の答えは-100≦y≦0で合ってますか?
>y=-4x2乗について、xの変域が-5≦x≦1のとき、yの変域を求めなさい という問題の答えは-100≦y≦0で合ってますか?
いいんじゃないかな。
ちゃんと0を最大値にできてるし
xとy両方の変域がわかってる時の、aの値の求め方はどうやりますか?
>xとy両方の変域がわかってる時の、aの値の求め方はどうやりますか?
問題にもよると思うけど、おそらく変域からaの正負がわかるかどうかがポイントなんじゃないかな。
0がyの変域に含まれていたらそこから判断するのかもしれない
関数y=-x2乗について
xの変域が-3≦x≦aのとき、
yの変域が-16≦y≦bである。
a b の値を求めなさい
この場合はどう解けばいいのでしょうか?
>関数y=-x2乗について
xの変域が-3≦x≦aのとき、
yの変域が-16≦y≦bである。
x=-3の時、y=-9だから、この時yは最小値-16にならないことがわかるね。
ってことは、x=aのとき、y=-16になるはずだ
xの変域が ー3 ≦x ≦2 のとき、2つの関数 y=2x+b, y=ax2乗 のy
の変域は同じになる。このとき、aの値を求めなさい。
この問題の解き方を教えてください!
>xの変域が ー3 ≦x ≦2 のとき、2つの関数 y=2x+b, y=ax2乗 のy
の変域は同じになる。このとき、aの値を求めなさい。
ポイントはxの変域が0を挟んでいることだ。
ってことは、二次関数のyの変域は、最大値か最小値のどちらかが0になるはず。
多分、2パターン考えられるんじゃないかな
最後の練習問題の【1】①は0小なりイコールy小なりイコール32「0」になるのに次は2小なりイコールy小なりイコール50と「2」になるのですか?
>最後の練習問題の【1】①は0小なりイコールy小なりイコール32「0」になるのに次は2小なりイコールy小なりイコール50と「2」になるのですか?
そうだね。
この問題のポイントは、xの変域が0をはさんでるかどうかだね。
はさんでいたら、yの最小値か最大値が0になる
かっこ一番
の2こ目の問題
右ですり
50なのに四十になります!
どうしたらいいか!?
>かっこ一番
の2こ目の問題
右ですり
50なのに四十になります!
どうしたらいいか!?
計算ミスかもしれないね。
もう一度x=5を代入してみよう
0≦x≦6 のとき
y=a x2 (エックスの二乗)
のa を求める問題がわかりません!教えてください
>0≦x≦6 のとき
y=a x2 (エックスの二乗)
のa を求める問題がわかりません!教えてください
aを求めるにはyの変域も必要かな!
関数y=x²において、xの変域が-3≦x≦2のとき、yの変域を求めよ。という問題の解き方を詳しく教えて下さい!
>関数y=x²において、xの変域が-3≦x≦2のとき、yの変域を求めよ
二次関数の変域の問題はトリッキーなのでグラフをかくといいよ。
この場合、xの変域が0を挟んでるから最小値に注意だね。
変域に0が入っていないとどうなるか教えてください
最後の問題の「1」の②と「2」の②の0が含まれていない計算は、どう解けばいいのか分からないので教えてください
>変域に0が入っていないとどうなるか教えてください
変域の端っこと端っこを関数の式に代入して、その時のyの値をそのまま変域にしよう。
念のために図を書いておこう
>最後の問題の「1」の②と「2」の②の0が含まれていない計算は、どう解けばいいのか分からないので教えてください
変域の端っこと端っこを二次関数に代入して、その時のyの値を求めてみよう。
あとはそのyを使ってyの領域の不等式を作ればいいよ
0を最小にするか最大にするかはどうやって見極めるんですか?
三角錐の表面積の求め方と体積の求め方を簡単に解説してほしいです