中学数学を攻略するために押さえたい3つのこと
中学校の数学をどのように勉強したらいいかわからない。
中学校の数学の授業が意味不明すぎてついていけない・・・
そんな悩みをお持ちではありませんか?? そんな悩みを解消するために塾に通ってみたり、進研ゼミに入会してみたりしてはいませんか。
ぼくは現在、25歳のいい大人になりました。10年前に勉強した数学の教科書を2日間をかけて復習してみました。やっぱり中学校を卒業してから10年たつと、色々忘れていました。いやあ、年をとるって怖いですね笑

そんな中学校三年間の数学を48時間で復習してみた結果、
中学で学習する数学で大切なことは3つしかない
ということに気づいたのです。3つですよ? 3つ。片方の指で数えられちゃいます。中学の数学の単元には図形とか文字式とか方程式とか関数とか山のようにありますが、どれも以下の3つを軸に解説されているのです。
- 定義(あるものごとの意味)
- 定理(あるものごとの性質)
- 解法(テストで点をとるためのコツ)
どんなに複雑なことを説明している数学の教科書でも、ゼッタイに上のいずれかを解説しているのです。今日は、中学の数学を攻略するために必要なの3つことを徹底解説していきます。よかったら参考にしてくださいね。
中学数学のコツ1. 「定義」を押さえる!
中学数学の教科書で解説されている1つの事柄のうち、
定義(definition)
というものがあります。デジタル大辞泉によると、
物事の意味・内容を他と区別できるように、言葉で明確に限定すること。
とあります。つまり簡単にいってしまえば、
あるものごとの意味・内容
のことですね。たとえば、りんごを例にとりましょう。
りんごの定義って??

「りんご」という言葉を耳にすると、以上のようなリンゴの写真を思い浮かべる方が多いのではないでしょうか??青森県に住んでいなくても、りんごの写真とかイメージを思い浮かべることができます。
しかし、「りんご」をまだ見た事がない人のために言葉で説明してほしい、と言われたらどうでしょう?? 今までそのような経験がありません。ぼくだったら苦し紛れに「えっと・・赤くて丸い甘い味のする果物・・・か、かな?」と説明するかもしれません。
この程度の説明では「りんご」を示しているのか、はたまた「熟したプラム」を説明しているのか検討もつきません。これではコミュニケーションを上手にとれていないことになります。
そこで登場するのが定義。りんごの定義(ものごとの意味)を確認してみましょう。デジタル大泉林によると、
バラ科の落葉高木。また、その果実。
とあります。植物をろくに勉強していないぼくにとって、正直、この定義はチンプンカンプンです笑 だがしかし、このりんごの意味の説明は、「りんご」だけをピンポイントに説明しています。ゼッタイに「熟したプラム」の説明と混同することはありません。これが定義の性質の一つである
言葉で明確に限定すること
の意味です。
中学数学の教科書に出てくる定義って??
それでは、中学数学の教科書に登場する「定義(ものごとの意味)」にはどのようなものがあるでしょうか?!?
りんごの定義ほどエキサイティングではありませんが、とりあえず確認してみましょう。
たとえば、中学2年生の数学の単元で学習する「対頂角 (Vertical Angle)」を例にとりましょう。
対頂角の意味(定義)は、TOMACの数学用語集によると、
2つの直線が交わったとき出来る4つの角のうち、向かい合った角
だそうです。図で表現すると以下のようになります。
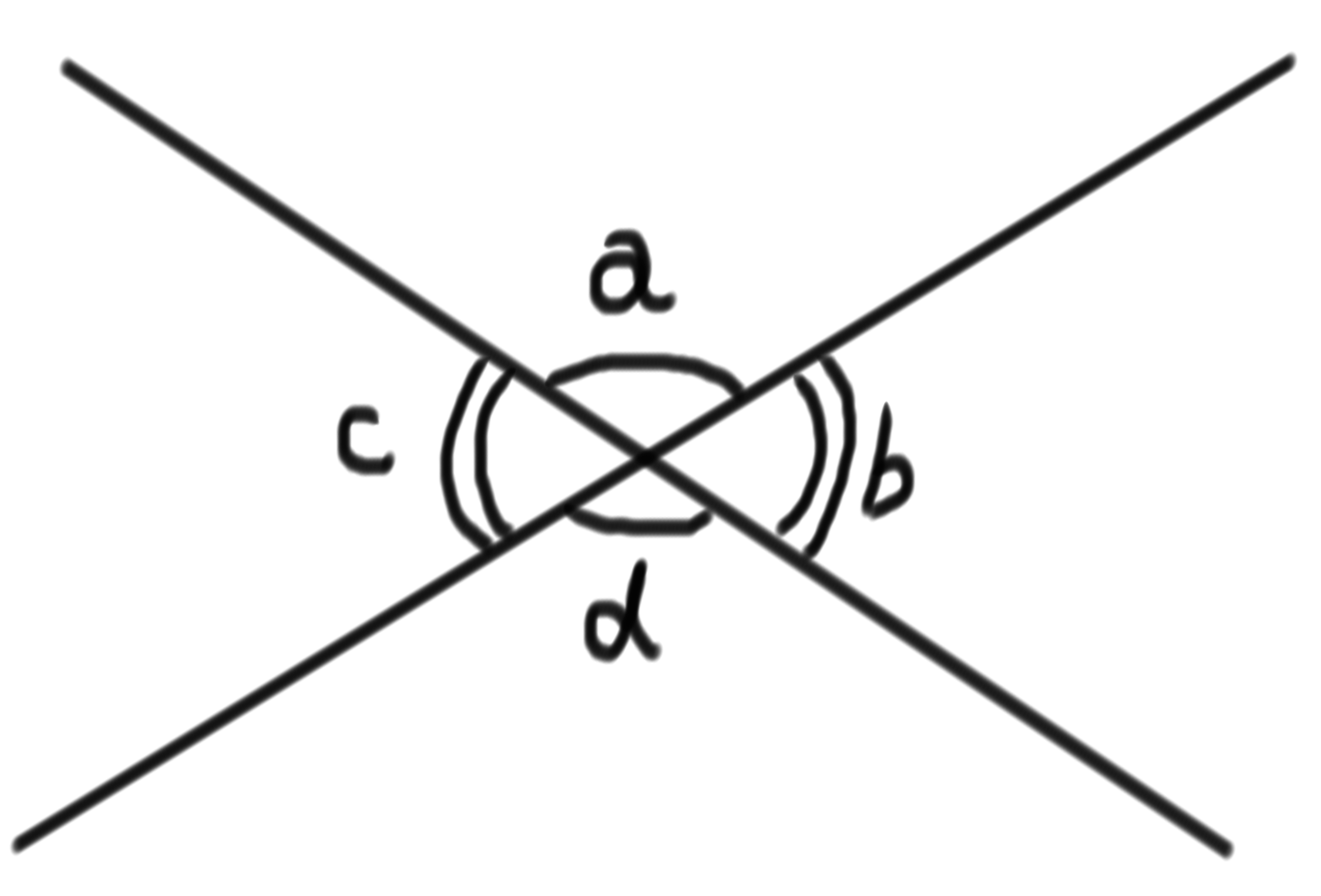
上の図でいえば、4つの角aとd、bとcがそれぞれ「対頂角」とよばれるわけですね。ふむ、かなり分かりやすい明確な定義です。定義の最大の特徴は、
定義には理由がない
ということです。なぜリンゴはリンゴなのか?? なぜ対頂角は対頂角とよばれるのか??
このような問いに答えはありません。強いて言うなら、
昔のお偉いさん方が勝手に決めたから
と答えるしかありません。それぐらい、数学用語もしかり、果物もしかり、定義にはゼッタイ的な権威があるのです。ごく少数の人間しか「定義」をいじることができません。
中学数学のコツ2. 「定理」を押さえる!
2つ目に中学校の数学で大切なことは「定理(theorem)」を押さえることです。定理とはデジタル大辞泉によると、
ある理論体系において、その公理や定義をもとにして証明された命題で、それ以降の推論の前提となるもの。
だそうです。ちょっと難しいので噛み砕いてみると、
定義(ものごとの意味)をもとにして証明されたこと
といえます。定義をもとにした事柄が定理というわけですね。中学校の数学教科書では「性質」と呼ばれていることが多いです。定義がなければ定理がない。定理がなければ問題が解けない。いわば、数学の問題をとくための道具(アイテム)のようなものです。
いまいちのピンと来ないです。先ほどの対頂角の例をもとに、定理を確認してみましょう!
対頂角の定理とは??
対頂角の定義は、
2つの直線が交わったとき出来る4つの角のうち、向かい合った角
でしたね。この定義から導くことができる定理は以下のものがあります。
対頂角は等しい
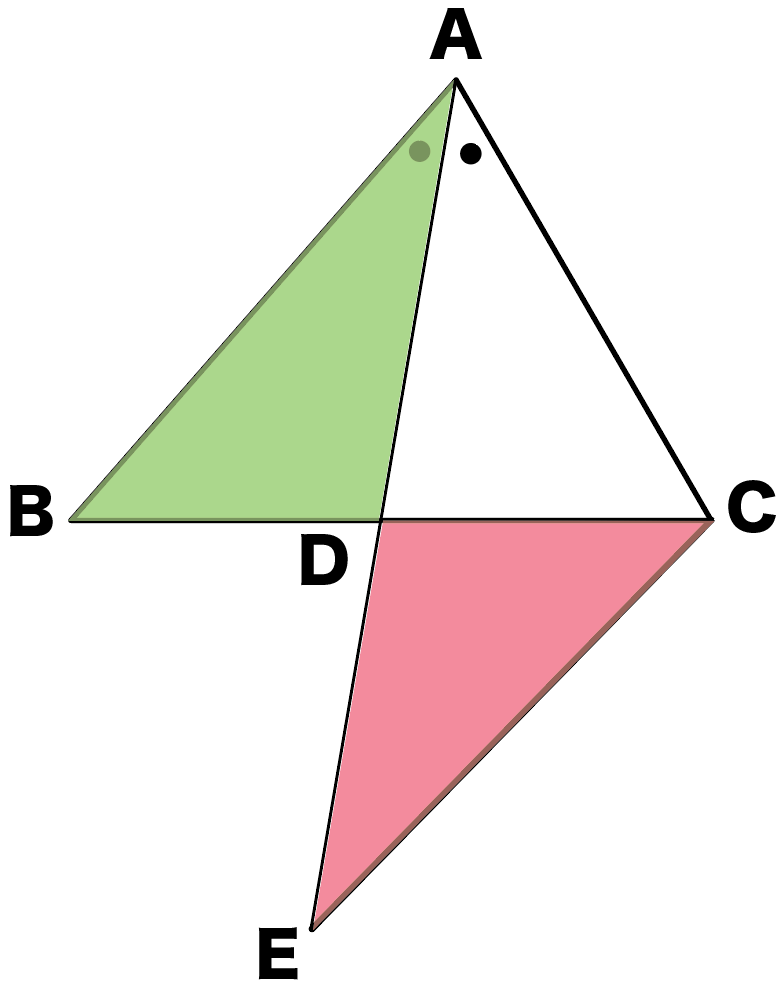
というものです。下の図でいえば、

角A= 角D
角B=角C
というわけです。すべての定理には理由があります。なぜこの対頂角の定理がいえるのか。その定理が存在できる理由を探ってみましょう。
これは、
直線の角度は180度である
ということから証明できます。
角aとc上の直線がつくる角度は180度であるため、
角a+角c = 180度・・・・(1)
角cと角dに関しても同様のこと言えるため、
角c+角d = 180度・・・・(2)
(1)と(2)より、
角a = 角d
よって、対頂角は等しいといえるわけですね!
この対頂角の例のように、
定理には必ず理由があります。中学数学の教科書では「性質」という用語で教えられることが多いです。「定理」とか「性質」のようなワードが登場したら、その理由について考察する癖をつけておきましょう。
なぜ定理が重要なのか??
定理には存在する理由があります。よって、暗記しなくても全く問題ありません。必要最低限の公理や定義を頭にいれておけば、自分で導くことができるからです。
ただし、
数学の定理をおぼえておくと無茶苦茶便利である!
ということを忘れないでください。定理をおぼえていない中学生は、毎回、定理を定義や公理から導かなくてはなりません。いわば、数学の定理はRPGゲームでいえばアイテム。ソードや盾。ポケモンでいったらワザマシンの役目を果たしています。あってもなくても構わないが、ないと不便で攻略に時間がかかる。そういう性質を定理は持っているのです。
中学数学のコツ3. 解法を使いこなせ!
中学数学を攻略する最後のコツは「解法」を使いこなすことです。
解法とは、
数学の問題を効率よく解くための方法
のことです。方程式の解法を例にとってみましょう。方程式を解法するために知っておくべきことは、
等式の性質
だけです。これだけあれば、中学数学で登場する大抵の方程式をとくことができます。がしかし、これだけでは中間テストや期末テストで登場するモンスター級の方程式を倒すことはできません。せいぜい、相打ちが良いところです。
テストでよりいい点数をとりたい。速く休み時間でキャッチボールをしたい。
そんな中学生たちのために、方程式に関する解法がいくつか用意されているのです。
- 解の公式(二次方程式)
- 乗法の公式(二次方程式)
- 代数法(連立方程式)
- 加減法(連立方程式)
- 移項(方程式全般)
これらを知らなくても方程式は解けますが、知っていたら超便利。これが中学数学で登場する「解法」というやつらです。テストでいい点をとりたかったり、クラスの美女を振り向かせたい方は数学の「解法」を暗記することをおすすめします。
数学の解法は、ポケモンやドラクエに例えると裏技です。セレクトボタンを7回おしてポケモンセンターにポケモンを預ける。などといった、一気にポケモンのレベルを上げることができるチート手のたぐい。裏技を知らなくてもポケモンは楽しめますが、あったらもっと速く攻略できる。そんな感じです笑
「定義」と「定理」と「解法」で中学数学を攻略しよう!
中学数学の各単元で学習する新しいことが、
定義なのか??
それとも、定理なのか??
それともそれとも、解法なのか???
ということを頭に入れておくとかなり吸収のスピードが異なります。数学というゲームを攻略する、という気持ちで中学数学を勉強していきましょう。この新しい用語はポケモンの名前なのか、ポケモンに技をおぼえさせるワザマシンなのか、それとも、一気にレベル100に到達するための裏技なのか。
そんな感じで、中学数学をこつこつと勉強していきましょうね。
それでは!
Ken

Qikeruの編集・執筆をしています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いでサイトを始めました。
























そもそも数学が無理