【中学数学】3点を通る円の中心の書き方がわかる3ステップ

3点を通る円の中心の作図の方法を知りたい？？

こんにちは！この記事をかいているKenだよ。花粉に敏感だね。

3点を通る円の中心

を作図したいときってあるよね？？

たとえば、つぎの問題が宿題にだされたときとかね ↓↓

例題

下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

 

見た目むちゃくちゃむずそう。。

だけど、基本をおさえちまえばサクっと作図できちゃうんだ。

今日はこの、

3点を通る円の中心の作図・書き方

を3ステップで解説していくよ。

よかったら参考にしてみて。

三点を通る円の中心の作図がわかる3ステップ

3ステップでかけちゃうよ。

1. 弦をかく
2. 垂直二等分線をかく
3. 交点をうつ

作図につかうのは、

• コンパス
• 定規

の2つだけだね。

例題をといていこう！

例題

下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

Step1. 弦をかく

まず弦をかこう。

隣り合った2点を直線でむすべばいいんだ。

例題でいうと、

• 点Aと点B
• 点Bと点C

だね？？

こいつらを直線でむすんでやると、こうなる↓↓

この直線たちが円の弦になるんだ。

2本ひけばステップ1完了！

Step2. 弦の垂直二等分線をかく

つぎは弦の垂直二等分線を作図しよう。

垂直二等分線を2本かけばいいんだ。

えっ。垂直二等分線の作図方法わすれた？？

そのときは垂直二等分線の書き方を復習してみて^^

例題でいうと、

まず点Aにコンパスの針をおいて半円をかく。

コンパスの脚の幅をキープしたまま、

今度は点Bに針をおく。

そして、半円をかく。

2つの半円の交点をむすぶと、点A・Bの垂直二等分線のできあがり！

今度は弦BCの垂直二等分線。

てきとうにコンパスの脚をひらいて、点Bに針をおこう。

そして、半円をかく。

脚の幅をキープして点Cに針をおく。

そして、半円をかく。

おなじように半円の交点をむすべばいいのさ。

それが垂直二等分線になる。

どう？？

垂直二等分線かけたかな？？

Step3. 垂直二等分線の交点をうつ！

最後は交点をうつだけ。

垂直二等分線がまじわっているところに、

ぽちっと点をうてばいいんだ。

その交点が「3点を通る円の中心」になるよ。

例題でもおなじ。

垂直二等分線の交点をうってやろう。

すると、こんな感じになる↓↓

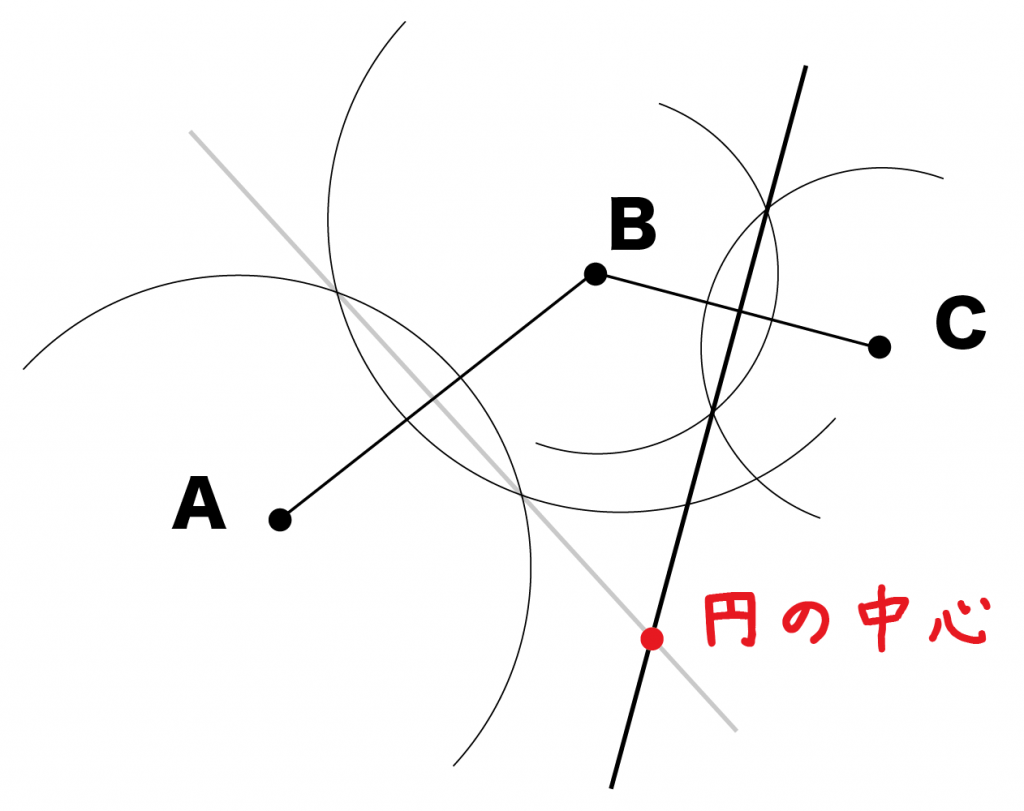
おめでとう！

この交点が「3点を通る円の中心」だよ^^

なぜ3点を通る円の中心が作図できるの？？

でもさ、

なんで「三点を通る円の中心」がかけちゃうんだろう？？？

都合よすぎるよね。

その理由はずばり、

「垂直二等分線上の点」と「端の点」同士の距離が等しいから

なんだ。

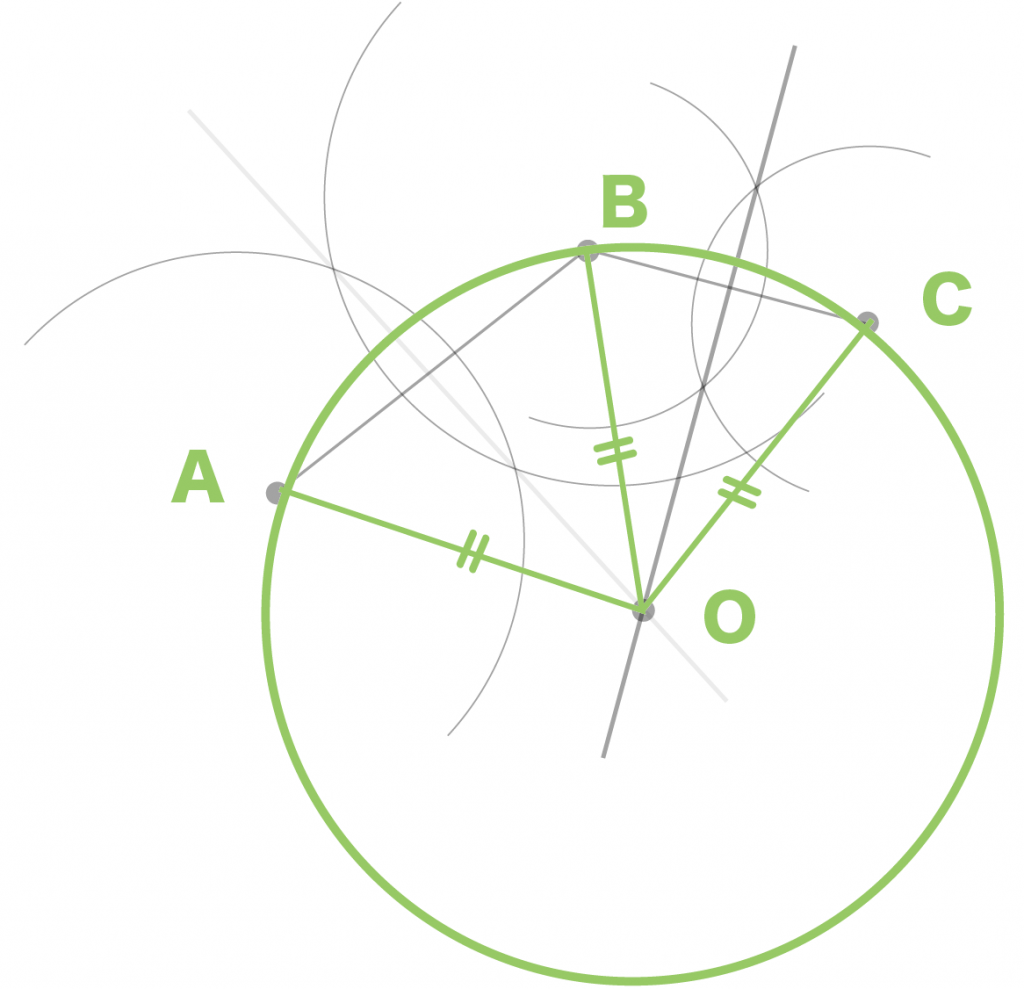
例題の円の中心をOとすると、

AO = BO = CO

になるってわけ。

つまり、

点A, B, Cたちは点Oからの距離が等しいってことだね。

円の定義は「ある点から等しい距離にある点の集合」だから、

3点を通る円が点Oを中心にかけちゃうってわけ。

えっ。なぜ、

「垂直二等分線上の点」と「端の点」同士の距離が等しくなる

のかって？！？

それは、垂直二等分線をかいてみればわかる。

たとえば線分ABの垂直二等分線をかいて、二等分線上の点をOとしよう。

ABと垂直二等分線の交点をMとするよ。

このとき、OMは垂直二等分線だから、

• AM = BM
• 角AMO = 角BMO = 90°

になる。

しかも、OMは共通だから、

2辺とのその間の角がそれぞれ等しい

という合同条件がつかえるね。

よって、

△AMO ≡ △BMO

になるわけだ。

対応する辺の大きさが等しいから、

AO = BO

になるんだ。

どう？？納得いったかな？？

まとめ：3点を通る円の中心は垂直二等分線で1発！！

三点を通る円の中心をかく

ってむちゃムズそう。

ただ、使うのは、

垂直二等分線だけ。

慣れてしまえば簡単なんだ。

テストまでに作図の練習をしてみよう^^

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。