三平方の定理で座標の2点間の距離を計算したい??
こんにちは!ぺーたーだよ。
今日は三平方の定理を使って、
座標上の2点の距離を計算する方法を勉強していこう!
関数が苦手な子は、
「えー、絶対やだ!」
とか思っちゃうかもしれないけど、
三平方の定理がしっかりわかっていれば、そんなに難しくないよ。
頑張ってやってみよう!
三平方の定理で座標上の2点間の距離を求める3つのステップ
三平方の定理を使えば、2点間の距離は3ステップで計算できるよ。
- 座標を書いてみる
- 垂線の交点をかく
- 三平方の定理を使う
次の例題を一緒に考えてみよう。
練習問題
2点A(-1,5), B(2,1)の間の距離を求めてください。
Step1. 図をかく
まずは座標と点を図にしてみて。
図がかかれてたらスキップしてもOKだけどね
練習問題でも図をかいてみようか。
まず、 座標軸をスラーっとかいてあげて、

2点の座標をポチッと打ってあげる。

だいたいこんな感じだよね。
直線ABを長さを求めるのが目標だ。
Step2. 直角三角形を作る
次は三平方の定理を使うために、
直角三角形を作ってみよう。
「求めたい2点の距離」を斜辺とする直角三角形を作ればいいのさ。
練習問題をみてみて。
ABを斜辺とする直角三角形を作るには、
2点から垂線を引いてやればいいね。
まず、Aからy軸と平行な垂線をひいてみて。
要はAから縦方向に線をひくんだ。

それがかけたら、Bからx軸に平行な垂線をひいてみて!
つまり、横方向の垂線ってことね。

そしたら、
2つの垂線の交点をCとしよう。

Cの座標はAのx座標、Bのy座標と同じだから、
(-1,1)
ってわけさ。

これで、 ABを斜辺とする直角三角形ABCがかけたね。

Step3. 三平方の定理で計算
最後は三平方の定理で斜辺を求めるだけ!
練習問題では、
ACは2点のy座標の差、
BCはx座標の差だよね??
つまり、
- AC=5-1=4
- BC=2-(-1)=3
になるはず。

あとはABをxとおいて、三平方の定理で計算すればいいね。
4²+3²=x²
こいつを計算すると、
x = 5
になる。
つまり、
AB = 5ってこと。

だからこの座標上の2点の距離は、
5
になるってことね。
おめでとう!
まとめ:座標上の2点間の距離は三平方の定理にお任せ!
座標の2点間の距離はゲットできたかな??
最後に解き方を復習しておこう。
- 座標を書いてみる
- 垂線の交点をかく
- 三平方の定理を使う
難しい作業もないから頑張ればできるはず。
グラフは書いた方がわかりやすいから忘れずに。
これでおしまい!
ぺーたー

静岡県の塾講師で、数学を普段教えている。塾の講師を続けていく中で、数学の面白さに目覚める

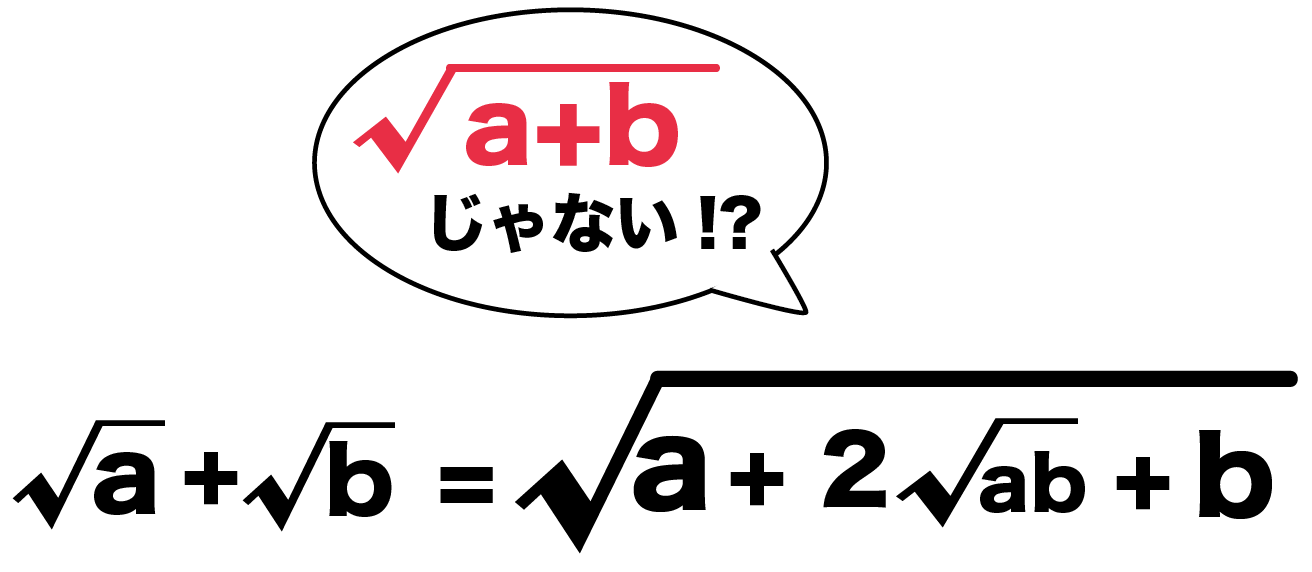



一辺が2cmの正方形ABCDを底面とし
他全て3mのせいしかくしい
oーABCDのへんOBをうごくpがある。
線分APが最小になるときを教えてください。
>一辺が2cmの正方形ABCDを底面とし
他全て3mのせいしかくしい
oーABCDのへんOBをうごくpがある。
線分APが最小になるときを教えてください。
APが最小になるのはAからOBに垂線を下ろした時の交点だね!
再び失礼いたします。
一辺が2cmの正方形ABCDを底面とし
他全て3mのせいしかくしい
oーABCDのへんOBをうごくpがある。
APCが正三角形になる場合
OP長さはどうなるのでしょうか?
>一辺が2cmの正方形ABCDを底面とし
他全て3mのせいしかくしい
oーABCDのへんOBをうごくpがある。
APCが正三角形になる場合
OP長さはどうなるのでしょうか?
まずはACの長さを計算して
正三角形の一辺の長さを算出してみよう
難しいです …!。゚(゚´Д`゚)゚。
あともう少しで私立入試なんですがどんな勉強をしたらいいのか分かりません。なにかいい勉強法はありますか⁇⁇
>あともう少しで私立入試なんですがどんな勉強をしたらいいのか分かりません。なにかいい勉強法はありますか⁇⁇
入試前は実践的な過去問や模試などを受けて応用問題になれるといいよ!
放物線y=x2乗 がある。点A,Bは放物線上にありABはX軸に平行。三角形AOBが正三角形になるときの点Aのy座標を求めよ。
を教えて下さい。
Aのx座標をaとして
AとBの座標をaで表してみよう。
そこから正三角形の一辺の長さと高さがaで表せるはず。
それを角度60度の直角三角形の比に当てはめてやればいいね
直線x=a(a>0)が放物線y=x2乗、直線y=2x-3と交わる点をそれぞれP,Qとする。
1.PQ=6のときのaの値を求めよ。
2.直線y=2x-3とy軸との交点をRとする。四角形ORQPが平行四辺形になるときのaの値を求めよ。
を教えて下さい
PとQの座標をそれぞれaで表してみよう!
それを使ってPQ=6という式を作ればいいね
2番はRQとOPの式をaで表して、そいつらの傾きが等しい(平行である)
っていうことを使ってaを求めてみよう
放物線y=1/4×2乗のグラフ上に3点A,B,cがあり、そのx座標はそれぞれ-4,2,6である。QはACの切片、点Pは線分AC上にあり三角形AOCと四角形AOBPの面積が等しい。
1.Pの座標を求めよ
2.Qを通り四角形AOBPの面積を二等分する直線の式を求めよ
を教えて下さい
放物線y=x2乗と直線y=2x+3が交点A,Bで交わっている。D,Cは放物線上の点でありCのx座標は2である。DCとABの交点をEとする。三角形ADEと三角形CEBの面積が等しいときDの座標を求めよ
も教えて下さい
>放物線y=1/4×2乗のグラフ上に3点A,B,cがあり、そのx座標はそれぞれ-4,2,6である。QはACの切片、点Pは線分AC上にあり三角形AOCと四角形AOBPの面積が等しい。
これは等積変形の応用問題だね。
OPとBCが平行になるようなPの座標を定めてやろう
>放物線y=x2乗と直線y=2x+3が交点A,Bで交わっている。D,Cは放物線上の点でありCのx座標は2である。DCとABの交点をEとする。三角形ADEと三角形CEBの面積が等しいときDの座標を求めよ
こいつも等積変形だね。
ABの座標を求めて、Cを通るy=2x+3と平行な直線を求めて、そいつの切片をy=2x+3で線対称にした直線が
Dを通ってy=2x+3に平行になっている、というヒントからDを求めよう
円がある。円周上にA,B,C,D,E(左回りで5つの点)があり、AEとBDの延長の交点をP、この円の周の長さをLとする。角APB=30,角PAC=40、孤AB+孤CE=1/2Lとするとき
1.孤ABの長さは
2.角ACBの大きさは
3.孤AB:孤CD:孤DEを求めよ
を教えて下さい
角CAEが140ということと、孤AB+孤CE=1/2Lを使ってみよう!
上の問題の3をもう少し詳しく教えて下さい。
ピンとこないときは三平方の定理を復習しておこう!
点Oは線分ABを直径とする円の中心である。点Cは円oの周上にあり孤AC=BCである。点Pは線分AB上にある点です。点Cと点Pを結んだ線分CPをPの方向に伸ばした直線と円Oの交点をQとする。点Aと点C、点Bと点Cをそれぞれ結ぶ。AO=10センチ、AP=15センチのとき三角形CQBの面積を求めよ。
を教えて下さい。