三角形の角の二等分線の性質の証明??
ある日、数学が苦手なかなちゃんは、
三角形の角の二等分線の定理の証明
に出会いました。
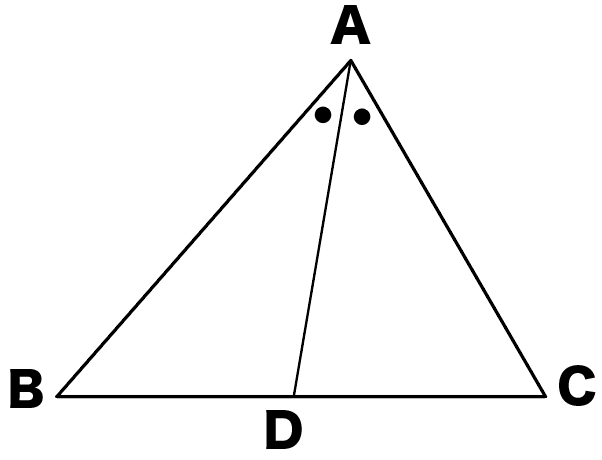
AB:AC = BD:DC であることを証明しなさい。
証明なんか、嫌いだ!
何で?
文章書くのむずい。。
確かに。
でも、数学の証明もやっぱり数学なんだ。
へっ?
どこが?
うーん、
スタートとゴールが明確なとこかな。
例えば計算問題だと?
問題を解くと、
答えにたどり着くってこと?
そう、証明も同じ。
証明すること
を見つけるのがスタートで、
証明できたらゴール!
ってこと。
道のり長そう……
ま、ってわけで。
二等分線の定理の証明のついでに、
証明にもなれちゃうおう。
この定理は知っておくと後々便利だよ。
……って言われても。。
三角形の角の二等分線の性質の証明がわかる5ステップ
三角形の二等分線の定理の証明は、
- 補助線をひく
- 相似な図形をみつける
- 辺の比に注目する
- 二等辺三角形をさがす
- 証明をかく
の5ステップだよ。
へー!
5つでいいんだね。
そうそう!
あっというまだよ!
それじゃあいくよー!
以下の図で∠BAD=∠CADのとき、
AB:AC = BD:DC であることを証明しなさい。

Step1. 「補助線をひこう!」
証明のために補助線をひこう!
証明の種をみつけるんだ。
えっと・・・・
補助線ってなに??
問題を解くのを
助けてくれる線だよ!
誰かが引いてくれるわけじゃないのかな……
そう!
残念ながら、
自分でひかなきゃいけないんだよね。。
ひー
今回ひく補助線は2本!
まず、ADをのばしまくる。
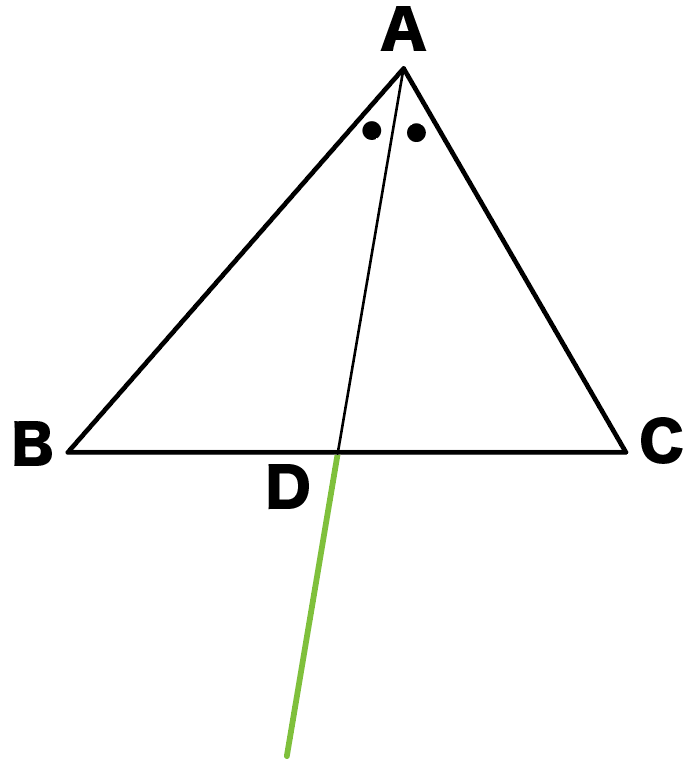
ほい!
もう一本は、
ABと平行で、
Cを通る直線をひくんだ。
この直線
と
ADの延長線との交点
をEとしよう。
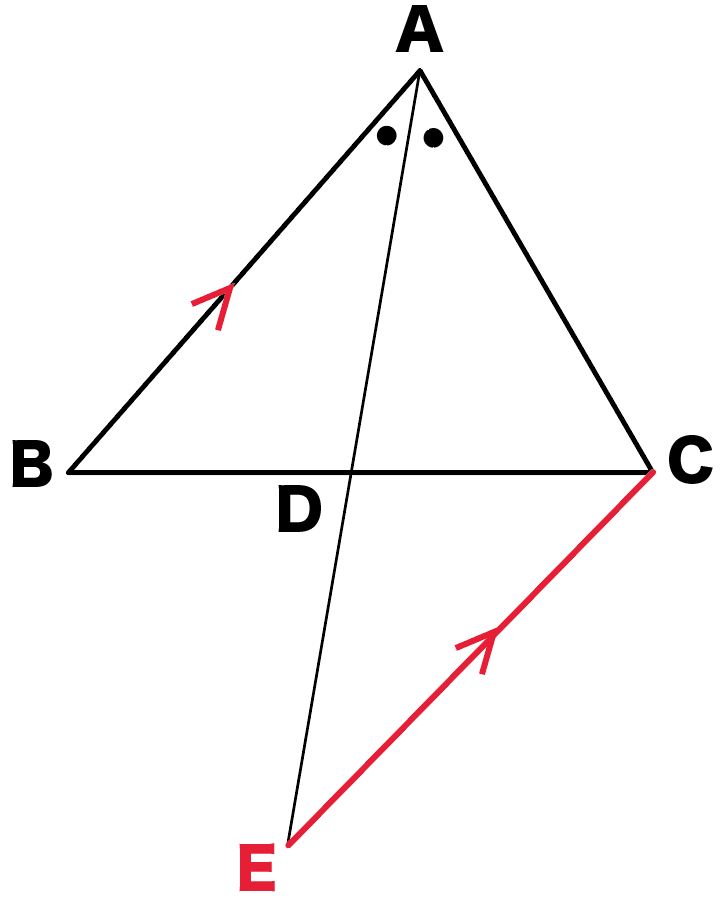
かけた!
書いた前後の変化を考えてみよう!
んー……、
あっ!三角形が増えてる!
そうだね。
いいところに気づいた!
増えた三角形
と
元の三角形
を見比べると……?
んー……、あっ!
Step2. 「相似な図形をみつけよう!」
相似な図形をみつけてみて!
△ABDと△ECDかな??
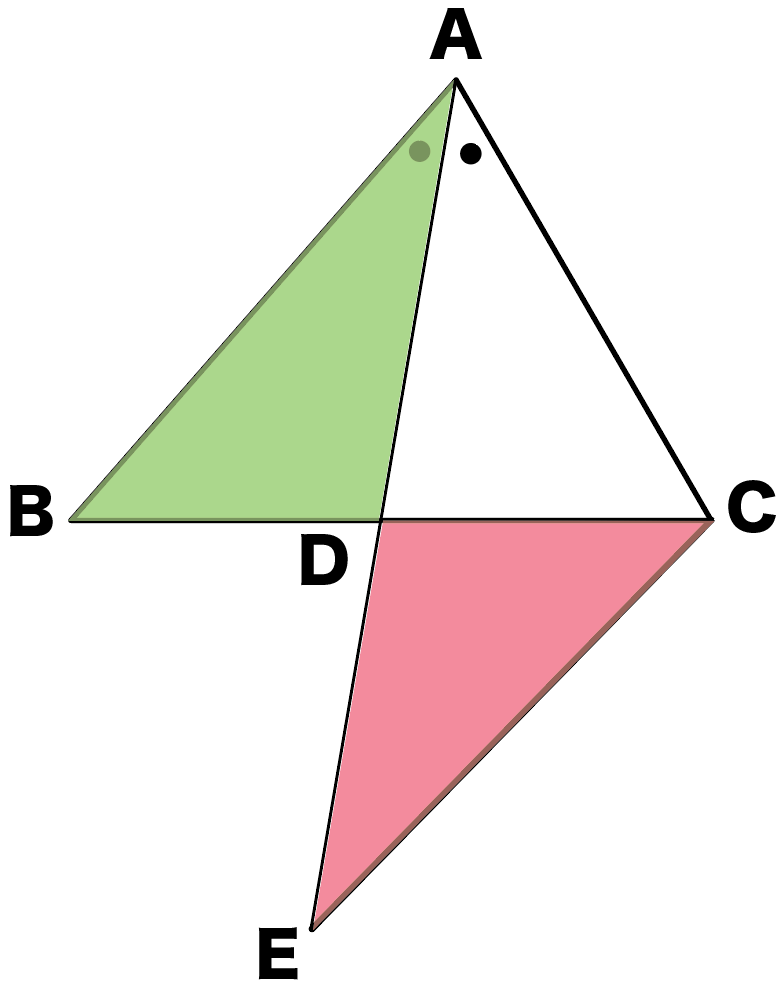
いいね!
覚えた相似条件と照らし合わせてみよう!
そ、相似条件…(遠い目)
ってなる人のために、
ちゃんと用意しといたよ!
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角がそれぞれ等しい
- 対応する2つの角がそれぞれ等しい
さすがは先生!
生徒のこと分かってる!!
できれば3秒で覚えてほしいけど、
慣れるまで書いておぼえてね。
えっと、この場合は……
注目ポイントは、
平行線!
あっ!
錯角だ!!
そうだね。
錯角が等しいから、
- ∠ABD=∠ECD
- ∠BAD=∠CED
だね。
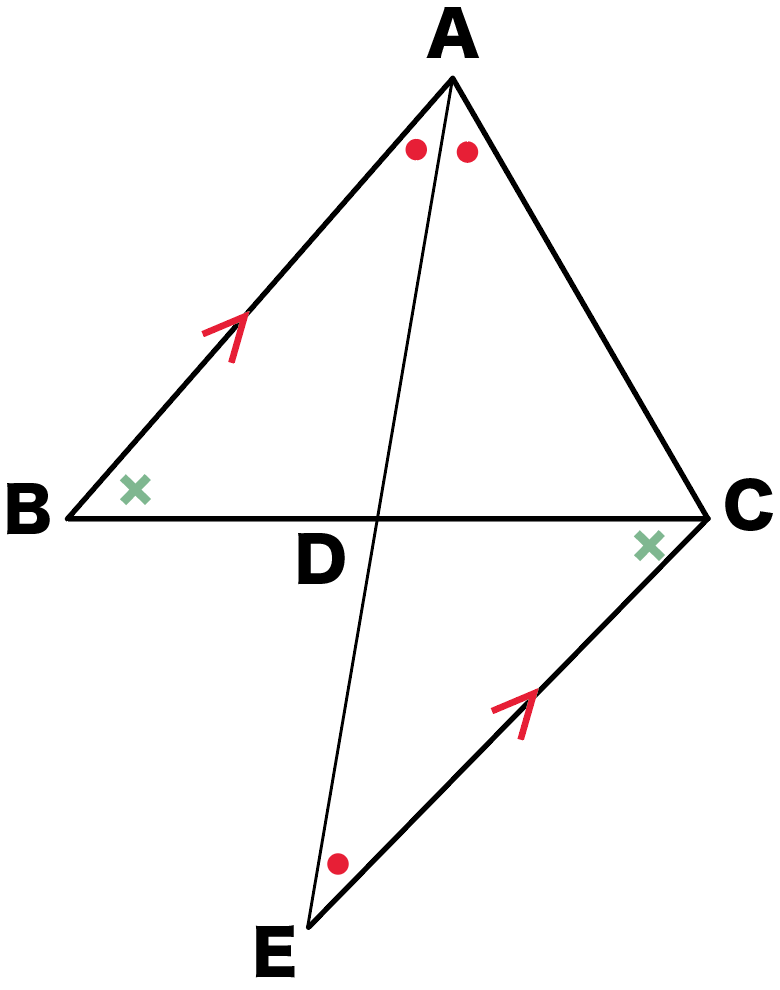
ってことは、
相似条件の3つめの、
2組の角がそれぞれ等しい
を使えばいいんだ!
そう!その調子!
△ABDと△ECDが相似
ってわかったから……
Step3. 「相似比を使おう!」
AB : CE = BD : DC・・・(1)
だ!!
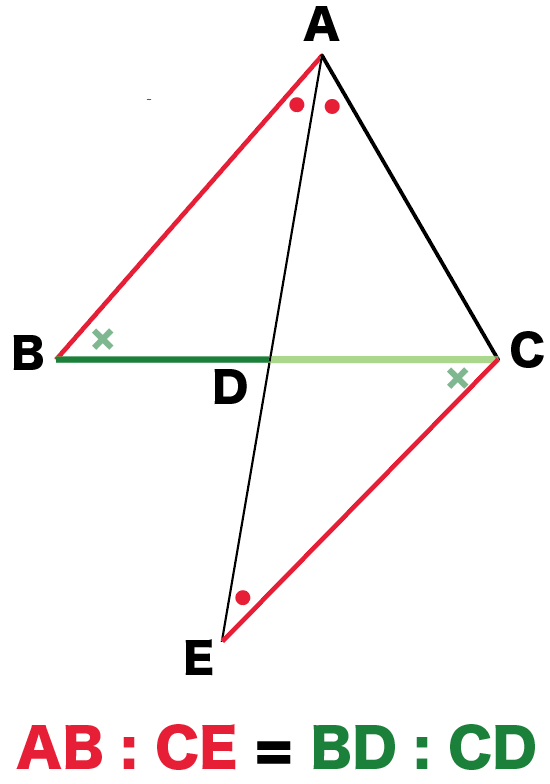
そうそう!
Step4. 二等辺三角形をさがせ!
つぎは、
二等辺三角形をさがしてみて!
にとうへんさんかくけい??
二等辺三角形になるための条件はおぼえてるー?
あ、
底角が等しくなる
じゃなかったっけ!?
お、それもあるね!
じゃあその条件つかおう。
二等辺三角形みつけられるかな??
あ!
∠CAE=∠CEAだから、
△ACEは二等辺三角形だ!!
ってことは、
AC = CE ・・・ (2)
になる。
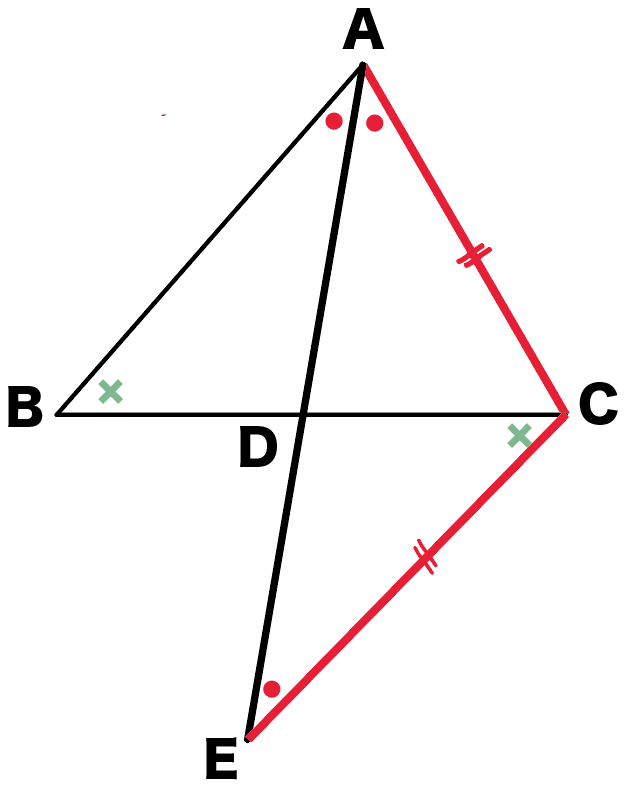
お、いいねー!
(1)と(2)から何が言える??
AB : EC = BD : DC・・・(1)
AC = CE ・・・ (2)
だから、、
あ。
AB : AC = BD : DC
ってことか!
そう!
これで証明したいことが見つけられたね!
やったー!
これで……
終わらないよ。
これから証明書くからね!
ひょええええええええ
Step5. 証明をかく
つぎは証明をかくよ。
いよいよね。
ういっす……
手順は簡単!
- 補助線の説明
- 相似の証明
- 比をつかった全体の証明
って感じだよ!
書けそうなとこからで大丈夫!
CからABに平行に引いた直線と、
ADとの交点をEとします。
△ABDと△ECDにおいて、
錯角が等しいので、
∠ABD=∠ECD…①
∠BAD=∠CED…②
①,②より、
対応する2つの角が等しいので、
△ABD∽△ECD
また、相似な図形では、
対応する辺の比が等しいので、
BD:DC=AB:CE
△ACEは二等辺三角形なので、
AC=CE
よって、
BD:DC=AB:AC
できた!!
どう??
おー!
やるじゃーーん
今までのことを書いた
って感じかも!!
いいね。
自分で見つけたことを証明に書けばいいの。
証明は準備ができれば、
難しいってわけではないんだ。
証明マスターになった気がする
そう、その調子!!
挑戦してるうちに慣れてくるよ。
まとめ:三角形の角の二等分線の定理の証明のポイント
おつかれさま!
三角形の角の二等分線の定理の証明は、
- 補助線をひく
- 相似な図形をみつける
- 相似比をつかう
- 二等辺三角形をさがす
- 証明をかく
の5ステップだったね??
難しいけど、
何度も挑戦してみようかな。
そう!その意気だよ!
うっす!

年齢不詳の先生。教育大学を卒業してボランティアで教えることがしばしば。








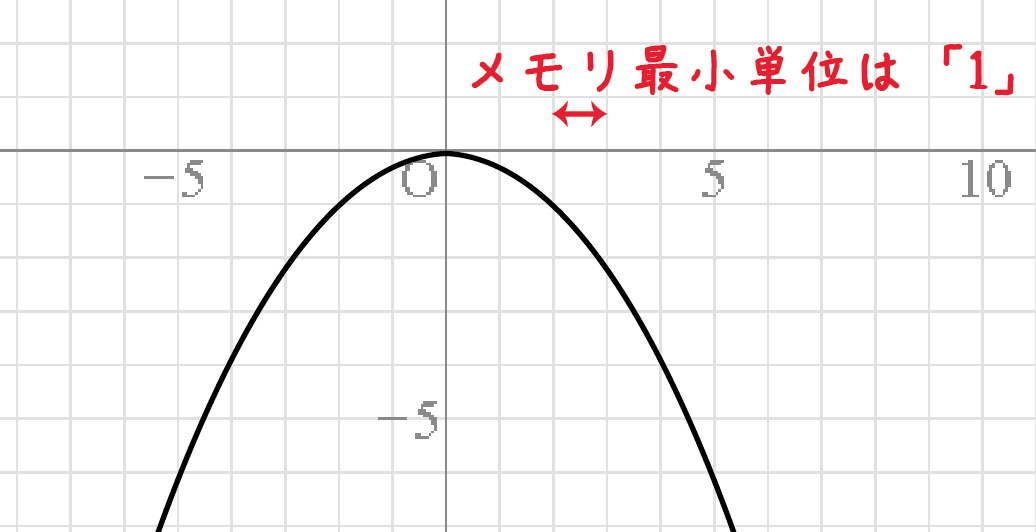

二等辺三角形を探さなくてもいいような気がしちゃいます…
正三角形ABCがあります。BC上の点pからACに垂線を引いて交点Qをつくる。
pを通り辺ACに平行な線をひいてABとの交点Rを作る。
PB:PC=1:2です。
AP QR の交点をsとして、三角形pqsの面積は三角形ABCの何分のいくつですか??
わかりにくいですが、お願い致します。
>正三角形ABCがあります。BC上の点pからACに垂線を引いて交点Qをつくる。
pを通り辺ACに平行な線をひいてABとの交点Rを作る。
PB:PC=1:2です。
AP QR の交点をsとして、三角形pqsの面積は三角形ABCの何分のいくつですか??
複数の三角形の面積比を使っていくよ。
△ABCの面積をaとして、まずは△APCの面積をaで表してみよう
数学の角の二等分線教えてください
>数学の角の二等分線教えてください
角の二等分線の作図の記事を読んでみて
ほのかっぺさんの問題で△apcの面積を表した後が分かりません…
>正三角形ABCがあります。BC上の点pからACに垂線を引いて交点Qをつくる。
pを通り辺ACに平行な線をひいてABとの交点Rを作る。
PB:PC=1:2です。
AP QR の交点をsとして、三角形pqsの面積は三角形ABCの何分のいくつですか??
角度に注目すると…
∠A=∠B=∠C=∠psq=60°
∠qps=30°
∠pqs=90°
辺の比に注目すると…
BP:PC=1:2
AS:SQ:QB=4:1:1
多分ここからは一人で行けると思います。
解答:1/18
二等辺三角形に酷似、ABの辺8.2mーBCの変9.8m。
角度30度のAC変の長さを出す時、AB+BC=18m 割る2=9m。1:2:3の3掛けるルート3で
約15mであってますか⁉️
補助線の引き方がわからないです。