循環小数を分数に変換したい!
こんにちは!この記事をかいているKenだよ。大根は干すとうまいね。
循環小数の問題でよくでてくるのは、
循環小数を分数に変換する問題
だ。
これは文字通り、
永遠につづく循環小数
を
分数
で表せって問題なんだ。

たとえば、こんな感じのやつね↓↓
例題
循環小数0.123412341234…..を分数で表しなさい。

求め方がわからんと苦戦する。
だけど、やり方はすごく簡単なんだ。
いっかいマスターすれば怖いものなしさ。
そこで今日は、
循環小数を分数になおす方法
をわかりやすく解説していくよ!
循環小数を分数に変換する3ステップ
3ステップでいけちゃうね。
- リピート数を数える
- 方程式をつくる
- 方程式をとく
例題をいっしょに解いていこう!
例題
循環小数0.123412341234…..を分数で表しなさい。

Step1. リピート数を数える
まずは、
繰り返しになってる数をかぞえてみよう。
例題の循環小数をみてみて。
0.123412341234…
は、
1234の「4ケタ」が繰り返えされてるね??

だから、リピート数は「4」だ。
あ、ちなみに、この循環小数はこうやって表せるんだ。
⇒くわしくは「循環小数の表し方」をみてみてね

これが第1ステップ。
Step2. 方程式を2つ作る
つぎは、方程式を2つたててみよう。
えっ。
そんなに方程式なんて立てられないって!??
そんなことはないよ。
じつは、
循環小数の方程式のたてかたはいつも同じなんだ。
もとの循環小数をx、繰り返しになってるケタ数をaとしよう。
このとき、
- 10^a X = 10^a × 循環小数
- x = 循環小数
っていう2つの方程式をつくればいいのさ。

例題で繰り返しになっている数は、
4ケタ
だったよね??
だから、a = 4 、循環小数 = 0.123412341234…を
10^a X = 10^a × 循環小数
に代入してやると、
10^a X = 10^4 × 循環小数
10000X = 10^4 × 0.123412341234…
10000X = 1234.12341234…
になるね。

んで、もう一個の式は、
X = 循環小数
のまんま。
X = 0.123412341234…
になるね。
よって、例題ででてくる2つの方程式は、
- 10000X = 1234.12341234…
- X = 0.123412341234…
だ!

Step3. 方程式を引き算する
つぎは、2つの方程式を引き算しよう。
「大きいほう」から「小さいほう」をひけばいいんだ。
つまり、
(Xに10のa乗をかけた方程式)-(Xの方程式)
っていう計算だ。

例題でも2つの方程式を引くと、
10000X = 1234.12341234…
– )X = 0.123412341234…
————————————–
10000X – X = 1234.1234… – 0.12341234…
9999X = 1234

になるね!
Step4. 方程式をとく
あとは方程式をとくだけ。
xだけの一次方程式だから簡単だね。
例題でも、
9999x = 1234
をといてみよう。
xの係数「9999」で両辺をわってやると、
9999x ÷ 9999 = 1234 ÷ 9999
x = 9999分の1234
になるね!

よって、循環小数0.12341234…は、
9999分の1234
って分数に変換できちゃうってわけ!

どう??
しっくりきたかな!?
まとめ:循環小数の分数変換に必要なのは一次方程式!
循環小数を分数に変換できた??
使ってるのは、中1数学でならう、
一次方程式の解き方
だけだ。
やってること自体は簡単だから、計算問題をたくさんといてみよう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。

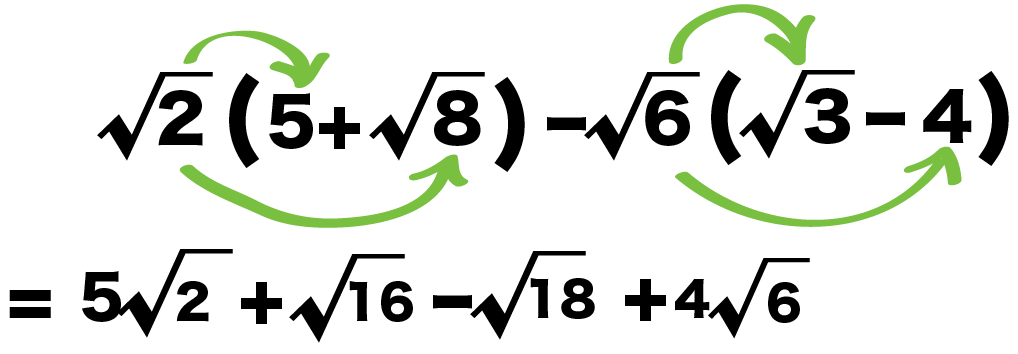






(ab+1)(a+1)(b+1)の因数分解を教えてください
>(ab+1)(a+1)(b+1)の因数分解を教えてください
もう因数分解できてるね!
循環小数で0.3858585…を分数にする方法
を教えてください(°_°)
>循環小数で0.3858585…を分数にする方法
まずは循環して何度も出現している小数の桁を見つけてみよう!
-3.972(循環してるのは7と2)
の分数への仕方を教えてください!!
>-3.972(循環してるのは7と2)
の分数への仕方を教えてください!!
まずはリピート数から探してみようぜ
なんで9999なの?教えてください
10000X – X
を計算すると9999Xになるからね!
約分できる時は約分しなくてはいけないのですか?
そうだね!
0.99・・・・・、1.99・・・・・など、〇.99・・・・・は、分数にできません。なぜですか。
できるよ!数字の後ろまで小数点が2つ移動できそうな場合は分母は100。
そして分子に数字をのせればいいね
しおんです。上記の質問は、
0.9・・・(9の循環)など、「少数以下が9の循環は分数にできません。」ということです。
例えば、0.9・・・は、1になってしまいます。
たしかにそうなるね。不思議
1の位があるときとかはどう表しますか?
1/9=0.111111…
9×1/9=9×0.111111…
1=0.999999…
詳しくは等比級数ね!
0.999…を分数に直すことだけど、
単純に9が連続するだけの単純循環だと、
0.999…=1-1/10^n (nは9の個数) だから 0.999…<1 で差は1/10^nなでは?
そして、例えば0.111…が1/9の分数から生じる分数由来の循環小数の場合は、
勿論、0.111…(1/9分数由来)の場合は この9倍は1 ですが
単純に 小数以下が1のが連続する単純循環の数ならば
0.111…=1/10-(1/9)/10~n となって、0.111…<1/9なのではないですか。
n→∞のとき、1/10^n→0 とおっしゃるかもしれませんが、大小関係は成立しますよね。
1/9=0.111111…は余りのある計算の連続ですよね。
いわゆる、分数由来の循環小数
ですので、
単に0.の次に1が連続する循環小数は
0.111111…=1/9(1-1/10^n)<1/9
なのではないでしょうか?
2021.03.31 滝ちゃんの質問
めっちゃわかりやすかったです!
助かりました!