【中学数学】式の展開の問題の解き方がわかる3ステップ

式の展開の問題の解き方がわからん！

こんにちは！この記事をかいているKenだよ。おしぼりはアツいほうがいいね。

中学3年生で最初にならうのは、

式の展開のやり方

だ。

一度マスターすればもう大丈夫。

どんな展開の問題もとけちゃう。

テスト前に身につけておきたいワザだね。

そこで今日は、

式の展開の問題の解き方

を3ステップで解説していくよ。

よかったら参考にしてみて^^

式の展開の問題の解き方がわかる3ステップ

さっそく解き方を紹介していこう。

つぎの3ステップでとけちゃうよ。

1. 乗法公式をつかう
2. 分配法則をつかう
3. 同類項をまとめる

いっしょに例題をといていこう^^

例題

次の式を展開しなさい。

(x+1)(x+3) -3 (2x +6)

Step1. 乗法公式をつかう

はじめに、

乗法公式がつかえるかどうか

を確認しよう！

公式がつかえる？？

じゃあガンガン使おうぜ。

例題をみてみると、

(x+1)(x+3)

で公式がつかえそうだね。

公式で展開してやると、

(x+1)(x+3)
= x^2 + 4x + 3

になるはず。

まず公式つかえるか確認。

いけそうなら公式をつかう。

これが第1ステップさ！

Step2. 分配法則をつかう

つぎは分配法則で展開してやろう。

（）をはずす

ってこと。

ゆっくり計算してみよう。

例題でいうと、後ろの、

-3(2x + 6)

で分配法則がつかえそうだね。

（）をはずしてやると、

-3(2x + 6)
= -3×(2x) -3 × 6
= -6x -18

になるね！

これが第2ステップ！！

Step3. 同類項をまとめる

最後に同類項をまとめてみよう。

同類項って、

文字と次数がおなじ項のこと

だったね。

たとえば、

• -6a
•  5a

とか。

文字はおなじで、

かけられている数が同じなら「同類項」というんだ。

例題では、

• 「4x」と「-6x」
• 「3」と「-18」

が同類項だ。

なぜなら、文字と次数が一致しているからね。

数字は数字同士が同類項になるよ。

同類項はまとめることができる。

係数同士をたしてやると、

• 4x -6x = -2x
• 3 -18 = -15

になるはず。

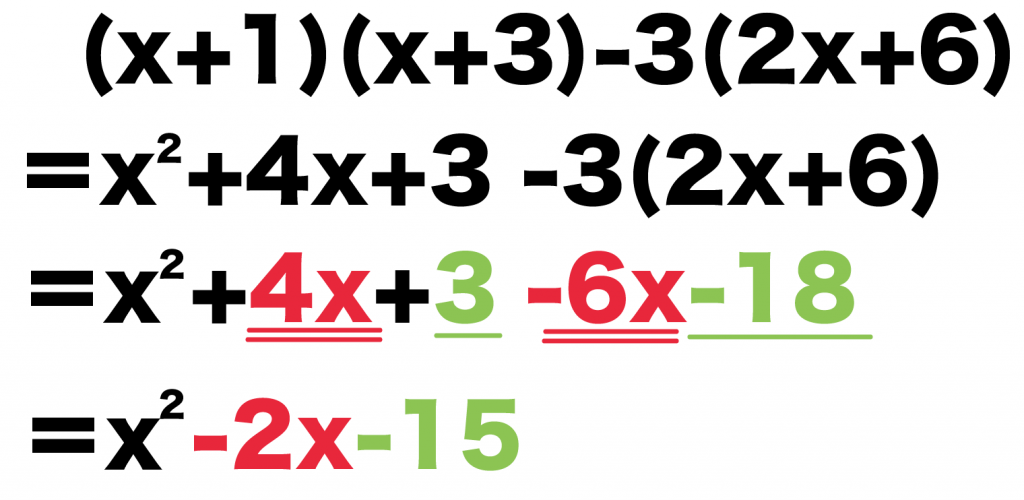
おめでとう！！これで式の展開が完了したよ^^

まとめ：式の展開の問題は公式と分配法則で一発！！

式の展開の解き方はカンタン。

1. 乗法公式
2. 分配法則
3. 同類項まとめる

の3ステップでいいんだ。

乗法公式おぼえるのが大変だけど、

問題をときまくっておぼえていこう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。