一次関数とは何者なのか??
こんにちは!この記事をかいているKenだよ。バジル、うめえ。
中学2年生になると、
一次関数
を勉強するね。
うーん、でもそもそも、
一次関数とはなんだろう!??
って思っちゃうよね。
正体不明のまま問題をとくのは無理。
エスパー能力があれば話は別だけどね。

そこで今日は、
一次関数とはなにか??
をわかりやすく説明してくよ。
よかったら参考にしてみてね^^
一次関数とは「関数の1種」だって!?
一次関数とは関数の1つ種のことだ。
ポケモンも600匹ぐらいいると思うんだけど、
ピカチュウはそのうちの1匹だよね?
それと同じさ。
「関数とは?」の記事で、
関数とは自動販売機である
ってたとえたよね。

一次関数は自動販売機の一種。
ってことは、アクエリアスしか売ってない自動販売機みたいなもんさ。

ここまではおっけい??
それじゃあ、一次関数とはどんな関数なの??
一次関数とはずばり、
y = ax + b
という形をした関数のことさ。

もう少しわかりやすく説明すると、
xが1回以下だけかけられた関数のことなんだ。
yの右側がxの一次式ならそいつは一次関数ってわけさ。
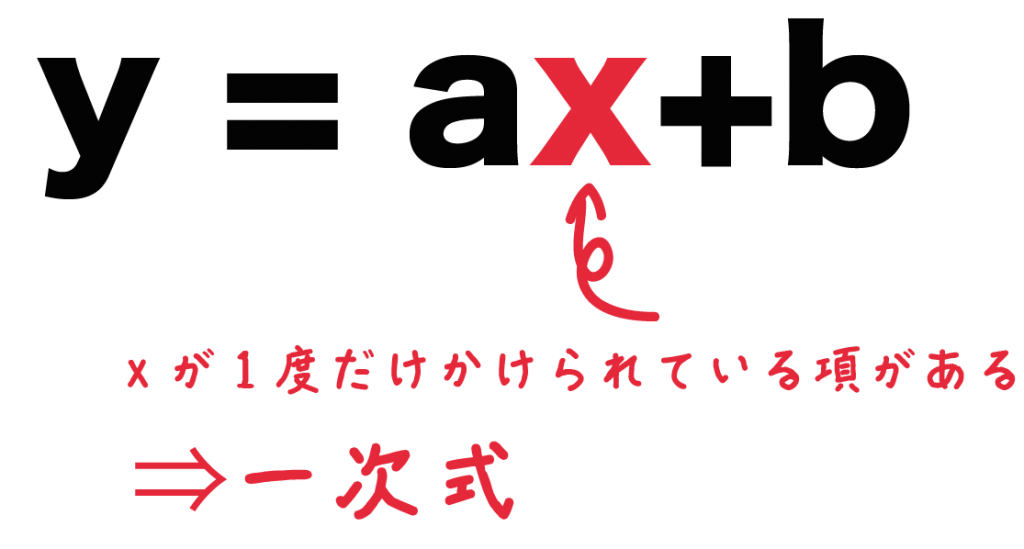
たとえば、
y = 9x
とか、
y = 9000x + 100
が一次関数になるよ。
だって、y = ax + bの形になっているし、xの項はすべて1次式だからね。
これさえ覚えておけば大丈夫。
一次関数を征服したようなもんさ!
えっ。比例と1次関数はどうちがうの??
ここで勘が鋭いヤツは、
比例は一次関数とどう違うんだよ?!
って逆切れしそうになっているはずだ。
うん、マジ鋭いね。
じつは比例は、
一次関数の1種なんだ。
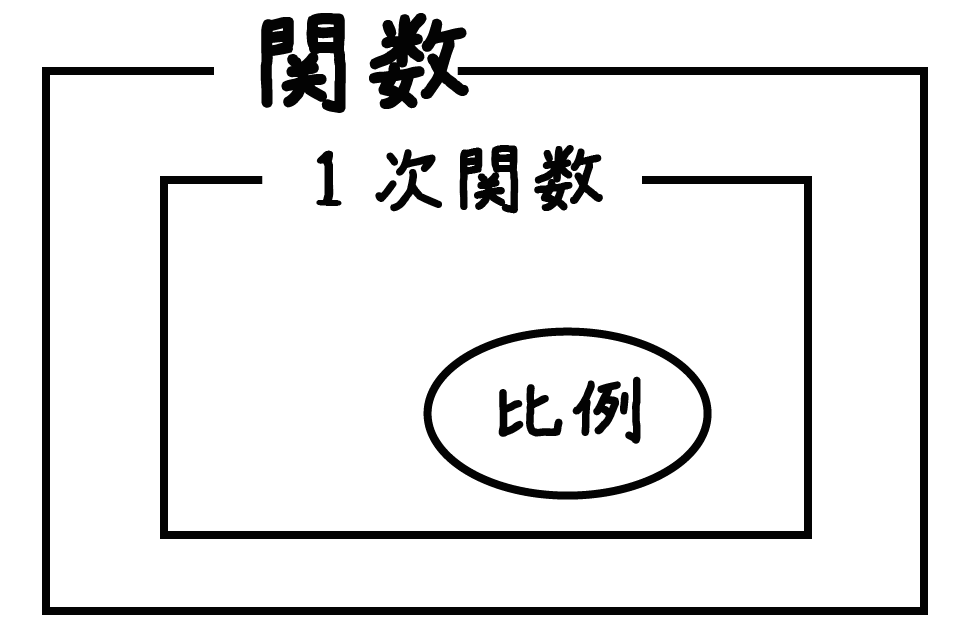
y = ax + b
のbがゼロになった一次関数が「比例」なんだ。
1次関数をさがせ!的な例題をといてみよう
だんだん「一次関数とはなにか??」ということがわかってきたかな。
つぎの例題をといてみよう↓↓
例題
yはxの関数で、つぎの式で表されるとき、一次関数であるものを選びなさい。
(a) y = 2x
(b) y = 4/x
(c) y = 5x^2+1
(d) y = 1/9x +8
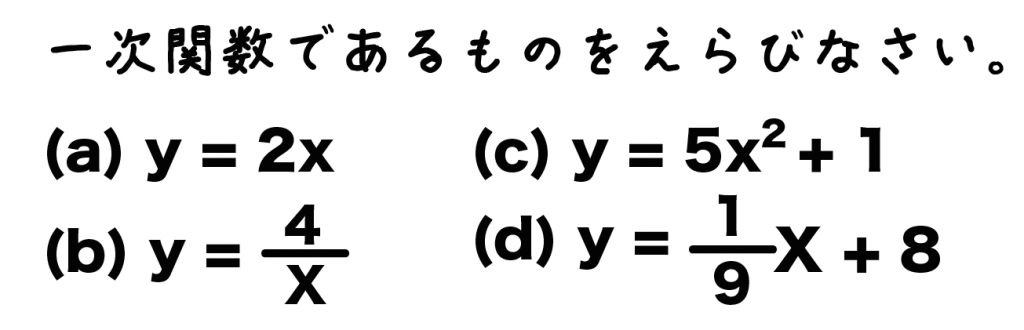
(a) y = 2x
こいつは一次関数だね。
なぜなら、xの次数が1だからね。y = ax + bのbが0のときのパターンさ。
こいつはまぎれもない比例野郎だ。
さっきもいったけど、
比例も1次関数の仲間ってことをおぼえておこう。
(b) y = 4/x
こいつは一次関数じゃない。
もうね、とんでもなく違う。
なぜなら、右辺がxで割られているからだ。
xがかけられているなら1次の項になるんだけど、割られているから違う。
xが「かけられてる」のか「わられている」のか把握しておこう。
わからないときは「反比例は一次関数??」っていう記事をよんでみてね^^
(c) y = 5x^2 +1
こいつも一次関数じゃない。
もうね。月とスッポンぐらい違うよ。
なぜなら、
xの項が「二次」だからだよ。
xが2回かけられているところに注意してね。
(d) y = 1/9x + 8
こいつは一次関数だ。
y = ax + bのaが分数でも一次関数だよ。
aの値にまどわされず、
xが何次の項になっているか??
とか、
y = ax + bの形の関数かどうか??
という判断基準でえらんでね!
まとめ:一次関数とは「xが1次式の関数」である
一次関数とはなにもの??
ってきかれたらどうする??
そう。
そうだよ。
一次関数とは「xが一次式の関数」だよ!
ってどや顔で答えてやろう。
自信満々で言えばみんな信じてくれるはずさ笑
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。








一次関数の図形の面積の解き方を教えて下さい。
動点の問題かな?
「【一次関数の利用】動点の問題の解き方がわかる3ステップ」を読んでみてね!
Xの増加量が6のときのyの増加量が-8で、x=-3のときy=5となる一次関数を求めなさい。
ってどうやるんですか?
>Xの増加量が6のときのyの増加量が-8で、x=-3のときy=5となる一次関数を求めなさい。
ってどうやるんですか?
xとyの増加量から変化の割合を計算してみよう!
変化の割合は傾き、つまり、y=ax+bのaのことだから、あとはxとyを代入してbを出せば一次関数の式がもとまるね
ありがとうございます!
y=5x-2の一次関数で、xの値が1から4まで増加したときの変化の割合を求めましょう という問題はどうやって解くのですか?
>y=5x-2の一次関数で、xの値が1から4まで増加したときの変化の割合を求めましょう
一次関数はxの増加量に関わらず変化の割合は一定だよ。
変化の割合は傾きのこと
y=-xはy=-1x+0としたら一次関数でしょうか?
>y=-xはy=-1x+0としたら一次関数でしょうか?
y=-xは次数が1だから一次関数だよ。
その中でもbが0の特殊な比例の関数ってやつなんだ。
一次関数が肉だとしたら比例は鶏肉だね
y=axは一次関数と言えますか?
>y=axは一次関数と言えますか?
次数が1だから言えるね
1次関数の問題を得意になるにはどうしたらいいのですか?
>1次関数の問題を得意になるにはどうしたらいいのですか?
基本を抑えることが大事。
一次関数はy=ax+bだから、この形さえ覚えておけばどうにかなるぜ
連立方程式の問題、どうすれば得意になれますか?
加減法をとりあえずマスターしておこう!
私はアメリカ在住の学生なのですが、functionを学校で習っているのですが全く理解が出来ず苦しんでいます。
一次関数のグラフも教えていただけますでしょうか。
何卒よろしくお願いします。
一次関数のグラフのかきかた読んでみて!
グラフから一次関数を見つけるにはどうしたらいいですか?
簡単な方法などあったらそれも教えてほしいです。
よろしくお願いします。
>グラフから一次関数を見つけるにはどうしたらいいですか?
一次関数は切片と傾きがわかればいいね。
まずy軸との交点から切片を出して、
あとは、座標が整数になる2点から傾きを計算すればオッケー
x+y=-5は、なんで、一次関数なんですか?
>x+y=-5は、なんで、一次関数なんですか?
xの次数が1だからね!
一次関数の変化の割合はどうやったら求められますか?
>一次関数の変化の割合はどうやったら求められますか?
yの増加量をxの増加量で割ればいいね
y=-2x+8 の変化の割合はなんですか
>y=-2x+8 の変化の割合はなんですか
変化の割合は傾きのこと。
つまり、y=ax+bのaだ
x=3の時y=-13, x=-1の時y=3
の一次関数はなんですか。これをまとめて一つの一次関数を求めるらしいんですけど…
>x=3の時y=-13, x=-1の時y=3の一次関数はなんですか
連立方程式の解き方がいいね。
y=ax+bに2パターンのxとyを代入して、aとbの連立方程式を作ろうぜ
グラフ上に、原点O、m…y=-2x-4、傾きが1/3の一次関数nがある。mがx軸と交わる点をAとし、nがy軸と交わる点をCとする。また、直線mとnの交点をDとする。このとき、四角形OACDをy軸を対象に一回転した時の体積を求めなさい。
かなり時間をかけたのですが中々溶けません。どのようなやり方をすればいいですか?
>グラフ上に、原点O、m…y=-2x-4、傾きが1/3の一次関数nがある。mがx軸と交わる点をAとし、nがy軸と交わる点をCとする。また、直線mとnの交点をDとする。このとき、四角形OACDをy軸を対象に一回転した時の体積を求めなさい。
多分、もう少しヒントがあるんだと思うんだけど、Dの座標を計算。
そして、OCDAをy軸に対照移動させて、回転体を作って見ると、
円錐+円錐台
になってることがわかるから、あとは根性で体積を計算してみよう
濃いめのスピカルさんへの回答が僕にはいまいち理解できません。
ワガママではありますがもう少し簡単に教えていただきたいです。
よろしくお願い致します。
>濃いめのスピカルさんへの回答が僕にはいまいち理解できません。
>Xの増加量が6のときのyの増加量が-8で、x=-3のときy=5となる一次関数を求めなさい
まずは「yの増加量÷xの増加量」で変化の割合を計算するんだ。
一次関数の変化の割合とは、傾きのことだから、y=ax+bでいうとaのことだ。
だから、あとはbを求めればこの一次関数の式が出るわけだね。
で、残るヒントの「x=-3のときy=5」をこの式に代入すると、bが求められるわけだ!
次の図の2直線ℓ、mの交点Pの座標を求めなさい。という問題で、答えが分数になるんですけど、私の答えが解答の分数と違っていたり、分子と分母が逆になっていたりするのです。解き方を教えていただけませんか?わがままですができるだけわかりやすくお願いします。長文失礼しました。
>次の図の2直線ℓ、mの交点Pの座標を求めなさい。という問題で、答えが分数になるんですけど、私の答えが解答の分数と違っていたり、分子と分母が逆になっていたりするのです。解き方を教えていただけませんか?わがままですができるだけわかりやすくお願いします。長文失礼しました。
交点の問題は連立方程式を使うのが一番楽だよ。
「2直線の交点の座標の求め方」を読んでみて
一次関数かわかりませんが・・・
次の二元一次方程式 ax+by=c(a,b,cは0でない定数)について述べた文で正しいのを選びなさい
ア xyの変域が自然数全体であるとき、この方程式の解は必ず1つである。
イ xyの変域が数全体であるときこの方程式の解は、yの値が常に同じ値である。
ウ xyの変域が数全体であるときxyの値の組(0,0)はこの方程式の解である。
エ xyの変域が数全体であるときこの方程式の解であるxyの値の組を座標とする点全体は直線になる。
長文すいませんこの問題がわかりません。解説お願いします。
一次関数( y=2x-1 )のグラフの書き方を教えてください!
>一次関数( y=2x-1 )のグラフの書き方を教えてください!
まずは切片の点を打ってみよう。
あとは、x=1の時の座標を打って、その2点を結ぶだけだよ。
詳しくは「一次関数のグラフのかき方」を読んでみてね
一次方程式4=7x+15を解きなさい。
>一次方程式4=7x+15を解きなさい。
xの項を左に、それ以外の項を右に移項してみよう!
最後にxの前の係数7で両辺を割ればいいね。
詳しくは「一次方程式の解き方」を読んでみて
Y=log xlf y=10 then,what is x?
A, 10
B, 1
C, 100
D, 10²
1次関数はある特定の一つなんですか?
1次関数をもう少しわかりやすく解説して欲しいですお願い致します
そうだね!
変域、定義域、値域のことについてもこのように詳しく説明してもらえませんか?
変数、定数、定義域、値域のことについてもこのように詳しく説明してくれませんか?
>変域、定義域、値域
変域の種類に、定義域と値域の2つがある。
定義域はxの変域のことで、値域はyの変域のことだね
おっけ〜
一次関数の判別でX=Y/3+4は一次関数となっていたのですがよく分かりません。解説には変形するとY=3X-12となるから〜…と書いてあったのですがどのようにしたらそのように変形するのかもわかりませんヾ(・ω・`;)ノよろしければ解説お願いします
>一次関数の判別でX=Y/3+4は一次関数となっていたのですがよく分かりません。解説には変形するとY=3X-12となるから〜…と書いてあったのですがどのようにしたらそのように変形するのかもわかりませんヾ(・ω・`;)ノよろしければ解説お願いします
両辺に分母の3をかけてみよう。
あとはyを左辺に、xを右辺に移項すればいいね
x=a
y=a
は一次関数ではないのですか?
>x=a
y=a
は一次関数ではないのですか?
そいつらは関数ですらなくて定数なんじゃないかな
グラフのy軸の交点やx軸の交点を求める問題全般がよくわかりません。やり方を教えてほしいです。
>グラフのy軸の交点やx軸の交点を求める問題全般がよくわかりません。やり方を教えてほしいです。
y軸と交わる時はx=0、x軸と交わる時はy=0を代入すればいいよ〜
y=10−x は一次関数ですか?
y=ax+b のかたちの一次関数はありますか?
>y=10−x は一次関数ですか?
そうだね!
3/xも一次関数と言えますか?
>3/xも一次関数と言えますか?
y=3分の1xってことだったら言えるね
120Lの水が入る水そうにA・B 2本の給水管がついて、A管では毎分3Lずつ、B管では毎分5Lずつ入れる事が出来ます。
20分間で水そうがいっぱいになるようにするには、A管で水を入れ始めてから何分後にB管からも水を入れ始めたら良いですか。
という問題を何度解いてもわかりません!教えて下さい!
ちなみにA管だけだと40分、A・B同時だと15分でした!
AB両方の管を使った場合の入れるスピード(毎分何L)を「A・B同時だと15分」という情報から計算しよう!
あとは「x分後にB管からも水を入れ始めた」として、
「20分間で水そうがいっぱい」になったという等式を作ってxを求めてやろう
ありがとうございました‼
ありがとう!!
一次関数の関係の例を教えてください。
y=ax+bの形をしている関数をあげてやればいいよ
すごくわかりやすいです!
y=5−x は一次関数ですか?
うん!そうだね
一次関数の連立方程式はありますか?
一次関数の連立方程式はありますか?
1次関数が使われている場所には、どのようなものがありますか?
一次関数の基礎がわからないんですが、基礎が書いてあるサイトとかって、ありますか?そもそも基礎がわからないので、、、
1次関数があるってことは 2次関数もあるんですか?
2次関数について教えてください!
ありがとうございます!!!
ワカリヤスカッタデス!!
ありがとうございます!!
またお願いします
自販機とかポケモンとかたとえがあってわかりやすかったです。またよろしくお願いします。
たとえばなどの例がすごく分かりやすくて良かったです‼︎
ありがとうございました!!
分かりやすかった泣
とてもわかりやすくて感謝です\(^o^)/
関数とか、一次関数っていうのは私すぐ忘れちゃって、授業で関数って言われたときに「あれっ?」ってなります(泣)
でも、このサイトはとてもわかり易くて、関数ははじめて見たんですけど、もう忘れなさそうです(*^^*)
3次関数ってあるんですか?
すごくわかりやすいです
ありがとう!!
これからもぜひ利用します!!!!
あるね