2乗に比例する関数ってどんなやつ?
みんな元気?「そら」だよ(^_-)-☆

今日は中学3年生で勉強する、
「2乗に比例する関数」
にチャレンジしていくよ。
この単元ではいろいろな問題が出てきて大変なんだけど、
まずは、一番基礎の、
2乗に比例する関数とは何もの??
を振り返っていこうか。
=もくじ=
- 2乗に比例する関数って?
- 2乗に比例する関数で覚えておきたい言葉
- 2乗に比例する関数のグラフは?
2乗に比例する関数とは??
中学3年生で勉強する関数は、
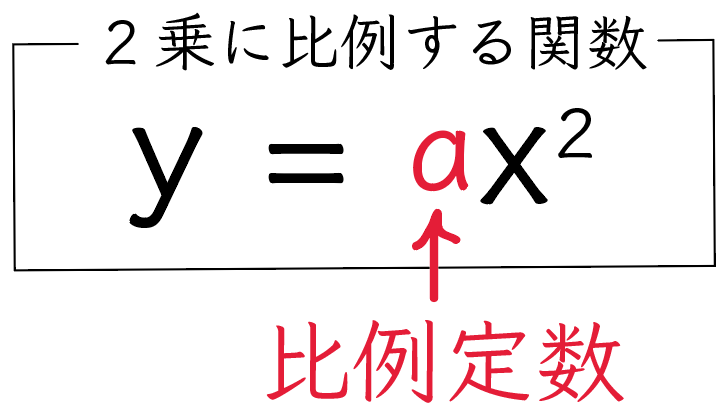
y = ax²
ってヤツだよ。

1年生で習った比例y=axの兄弟みたいなもんだね。
xが2乗されてる比例の式だ。
この関数にあるxを入れてやると、
2乗されて、それにaをかけたものがyとして出てくるんだ。
たとえば、aが6の場合の、
y = 6x²
を考えてみて。
このxに「3」を入れてみると、
「3」が2回かけられて、そいつにaの「6」がかかるとyになるよね?
だから、x = 3のときは、
y = 6×3×3 = 54
になるね。

こんな感じで、
関数がxの二次式になっている関数を、
2乗に比例する関数
って呼んでいるんだ。
2乗に比例する関数で覚えたおきたい言葉って?
2乗に比例する関数って形がすごいシンプル。
覚えなきゃいけない言葉も少ないんだ。
たった1つでいいよ。
それは、
っていう言葉。
これは中1で勉強した比例の「比例定数」と同じだよ。
2乗に比例する関数の中で、
xがいくら変化しても変わらない数を、
比例定数
って呼んでるんだ。
y=ax²
の関数の式だったら、
a
が比例定数に当たるよ。
y = 6x²
だったら、「6」が比例定数ってわけだね。

問題でよくでてくるから、
2乗に比例する関数の比例定数をいつでも出せるようにしておこう。
2乗に比例する関数ってどんなグラフになる?
じゃ、2乗に比例する関数のグラフを描いてみよう!
y = ax²のa、x、 yを表にまとめてみよっか。
比例定数aの値が、
- 1
- -1
- 2
- -2
の4パターンの時のグラフをかいてみるね。
>>くわしくは二次関数のグラフのかき方の記事を読んでみてね。
まず、xとyが整数になる時の値を考えてみると、

こうなる。
これを元に二次関数のグラフをかいてやると、

こうなるよ。
なんか山みたいでしょ?
こういうグラフを「放物線」と読んでるんだ。
グラフの特徴としては、
- aが正の時、放物線は上側に開く。
- aが負の時、放物線は下側に開く。
- 放物線の頂点は原点
- y軸に対して線対称
っていうのがあるよ。
>>くわしくは放物線のグラフの特徴の記事を読んでみてね。
まとめ:2乗に比例する関数はシンプルだけど今までと違う!
2乗に比例する関数はどうだったかな?
基本は1年生のときの比例と変わらないよね?
おさえておくべきことは、
- 関数の基本形 y=ax²
- 比例定数
- グラフ
の3つ。
基礎をしっかり復習しておこう。

そんじゃねー
そら

数学が大好きなシステムエンジニア。よろしくね!




yがXの二乗に比例し、xが2〜5まで増加するときの変化の割合が14であるような関数の式ってあるんですけど意味がわかりません。
>yがXの二乗に比例し、xが2〜5まで増加するときの変化の割合が14であるような関数の式ってあるんですけど意味がわかりません。
二次関数の変化の割合の公式を使ってみて!
yはxの2乗に比例し、x=-3のときy=18である。このとき、yをxの式で表わせ。
という問題はどうやって求めますか?
>yはxの2乗に比例し、x=-3のときy=18である
y=ax2の式にxとyを代入してaを求めてみよう。
詳しくは「二次関数の比例定数の求めかた」を読んでみてね
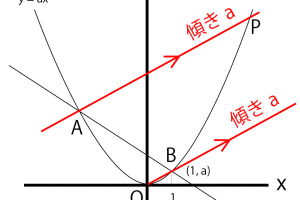
関数のグラフ上の、2点A、BのX座標が-2、4ので直線ABの傾きが3分の2の時のAの値とは?
>関数のグラフ上の、2点A、BのX座標が-2、4ので直線ABの傾きが3分の2の時のAの値とは?
xの増加量を求めて、変化の割合の公式を使ってyの増加量を求めてみよう!
日常の例はありますか?
よくある質問はありますか