たすき掛けの因数分解は便利!
こんにちは!この記事をかいてるKenだよ。クロアチアに住みたいね。
たすき掛けの因数分解はむちゃ便利。
因数分解の公式が使えないときとか、
共通因数をくくりだせないときとかね。
ほんとうに重宝するぜ。
だがしかし、さ。
なぜ、たすき掛けで因数分解できちゃうんだろう??
やり方が複雑すぎる。
ぶっちゃけ、怪しいんだよね。
信用できない。
そこで今日は、
なぜたすき掛けの因数分解が使えるのか??
をわかりやすく解説してみたよ。
よかったら参考にしてみて。
なぜ、たすきがけの因数分解の仕方がつかえるの??
さっそく、たすき掛けの因数分解を証明してみよう。
ax^2 + bx + c
を例として因数分解してみよう!

Step1.因数分解できちゃったことにする
まずは、たすき掛け因数分解したい式を、
うまーく因数分解できちゃったことにしよう。
とりあえずね。
さっきの例でいうと、
ax^2 + bx + c
を、
(Ax + B)(Cx + D)
に因数分解できちゃったことにすればいいんだ。

でも、これは「とりあえず」だよ。
Step2. かりの姿を展開しちゃう
さっき据え置きした、
(Ax + B)(Cx + D)
を展開しちゃおう。分配法則ですーっと()をはずせばいいんだ。
こいつを展開してやると、
(Ax + B)(Cx + D)
= ACx^2 + ACx + BCx + BD
= ACx^2 + (AD+BC)x + BD
になるね!

Step3. もとの式とくらべる
つぎは、
- かりに展開した式
- 元のオリジナルの式
をくらべてみよう。
さっきの例でいうと、
- ACx^2 + (AD+BC)x + BD
- ax^2 + bx + c
の2つだね。
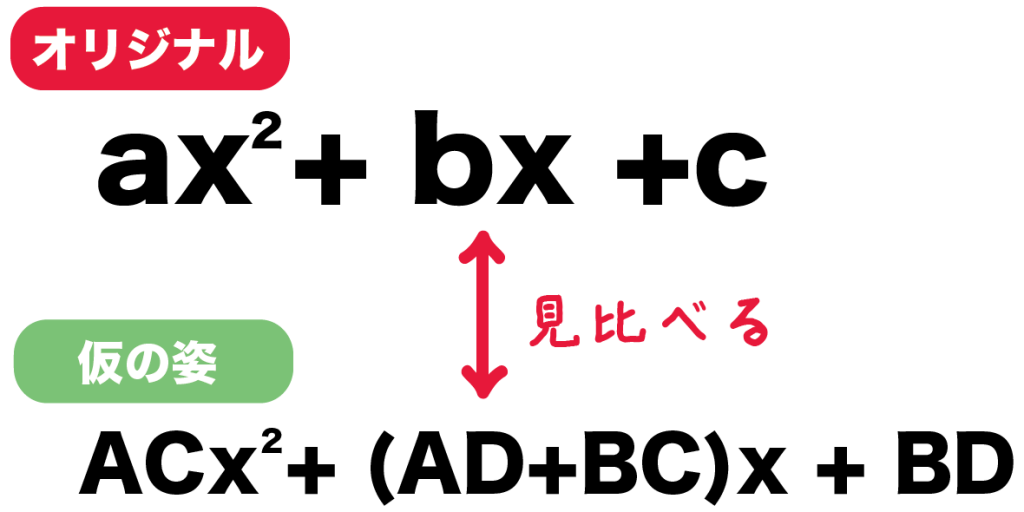
こいつらは「かりの姿」と「オリジナル」の式。
まるまる同じ式のはずだ。
だから、
- xの二乗の係数
- xの係数
- 定数項
は一致するはずなんだよ。ゼッタイ。

っていうことは、
- a = AC
- b = AD+BC
- c = BD
になるはずだね。
Step4. たすき掛けの登場!
あとは、仮に置いた文字の正体をあばくだけ。
- a = AC
- b = AD+BC
- c = BD
になるようなA・B・C・Dの組み合わせをみつければいいんだ。
で、でも、どうやって??
って思うよね。
そこで、だ。
たすき掛けマシーンの登場だね。
まっすぐな線をかいて、

xの二乗の係数、定数項、xの係数の順番にならべてやる。
ax^2 + bx + c
でいうと、
a、c、b
の順番だね。
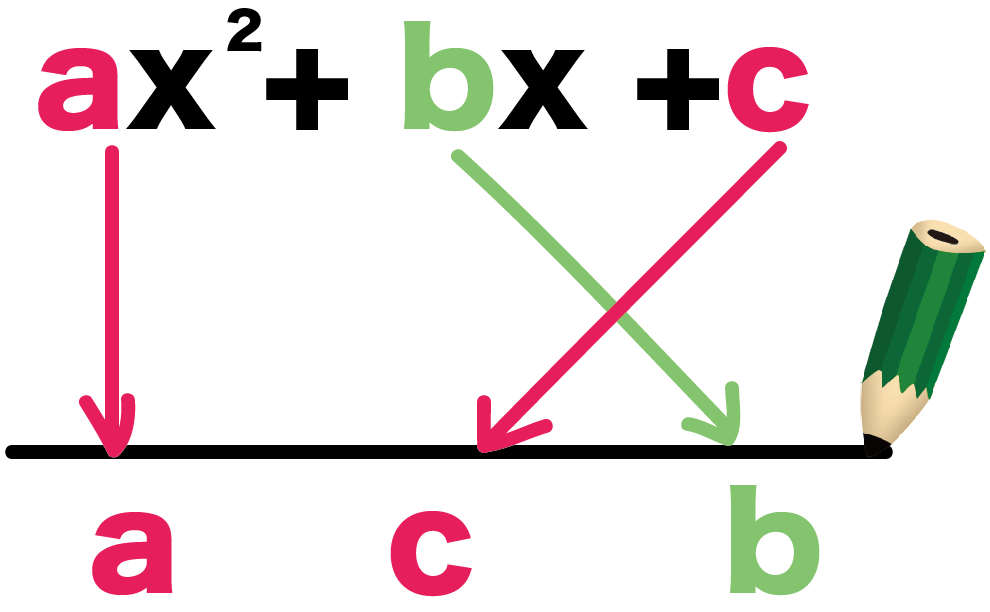
「かけたらaになる2つの組み合わせ」をaの上に、
「かけたらcになる組み合わせ」をcの上におこう。
今回は、
- a = AC
- c = BD
だったから、

こんなかんじになりそうだ。
ただ、今回はもう1つ条件がある。
そう。
b = AD+BC
だったね。
こいつをみたすためには、
4つの数字をたすき掛けのかけ算をして、それぞれたしたらbになるか??
ってことをたしかめればいいよね。

つまり、
AD + BC = b
になってればいいわけだ。
これならうまく、
- a = AC
- b = AD+BC
- c = BD
をみたすA・B・C・Dを求められるね!

たすき掛けの因数分解では、
- x2乗の因数
- 定数の因数
をイメージして、たすき掛けをしたらxの係数になればいいんだ。
どう??すっきりしたかな??
まとめ:たすき掛けの因数分解は据え置きで納得!!
たすき掛けのやり方は複雑。
正直わからないし謎だ。
だけど、因数分解できちゃうと仮定すれば大丈夫。
腐らずたすきをかけていこう。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。



質問する