中学数学の確率の求め方・公式・計算式をおしえて!
こんにちは!この記事をかいているKenだよ。3Dメガネを2つ買ったね。
確率の公式・計算式は正直、たくさんある。
だけど、中学数学ではたった1つの公式で大丈夫。
どんな確率問題もとけるようになるんだ。
あることがら「A」がおきる確率の求め方は、
つぎの公式で計算できちゃうよ。
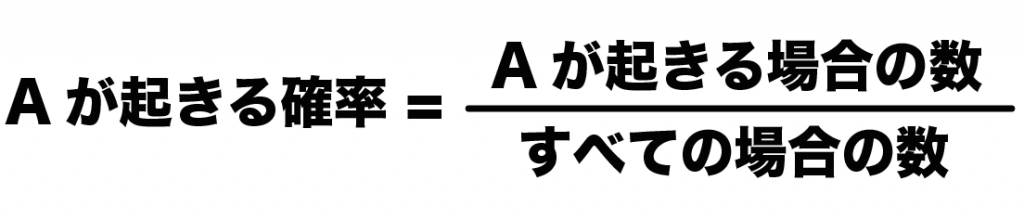
(Aが起きる場合の確率) = (ことがらAが起きる場合の数)÷(すべての場合の数)
だ。
もうちょっと公式っぽくしたい。
そんなときは、
- Aが起きる場合の数:a
- すべての場合の数:n
- Aが起きる確率:P(A)
としよう。
すると、
P(A) = a/n
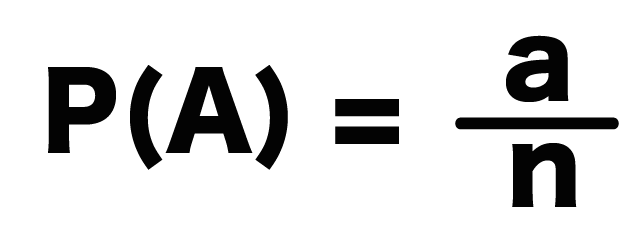
ともあらわせるね!
確率の求め方を実践!公式・計算式をつかってみよう!
さっそく公式をつかおう。
たとえば、コインを3回なげたとする。

このとき、3回とも表になる確率を計算してみよう。
3回なげたときの場合の数は??
3回コインをなげたときの場合の数をもとめよう。
表・裏のパターンはぜんぶで何通りあるかな??
ってことを数えていくんだ。
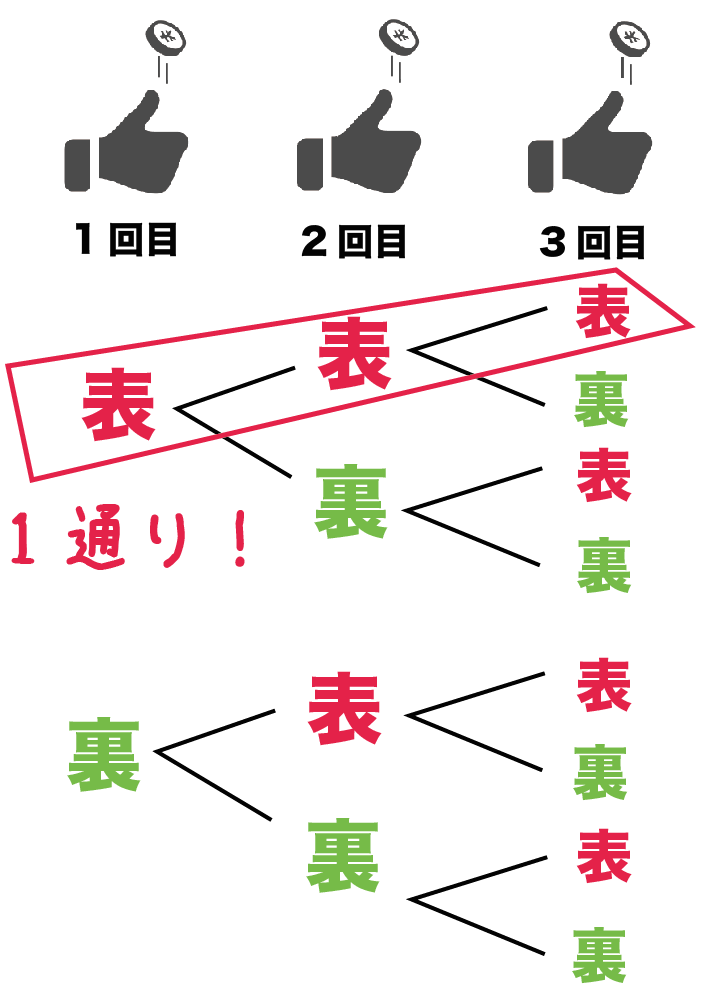
樹形図をかいてみよう。
1枚目が「表」だったら、つぎは「表」か「裏」。
2枚目も「表」がでたら、そのつぎも「表」か「裏」・・・・
というように考えていくよ。
すると、こんな感じの樹形図がかけるはず!
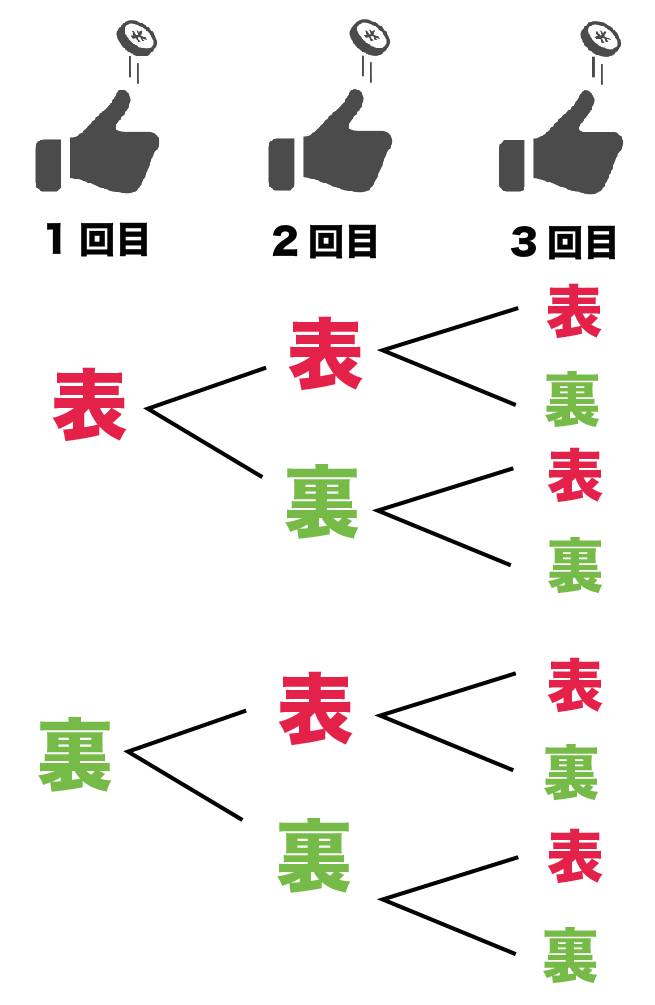
コインを3回なげたときの数は右のやつをかぞえてね。
すると、
8通り
あることがわかるはず。
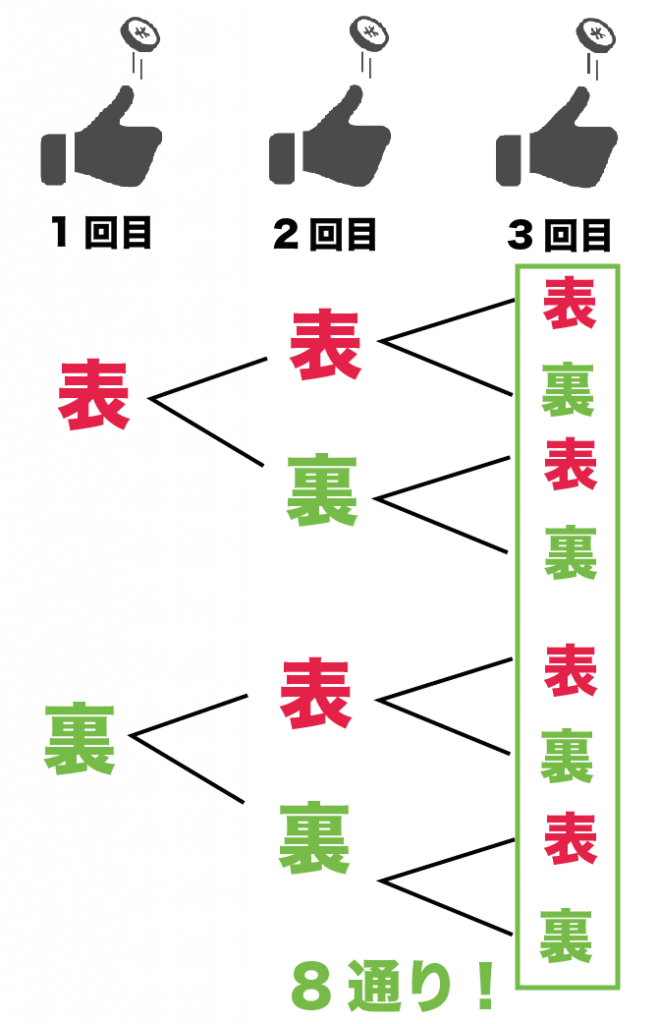
つまり、確率の求め方の公式の「n」が「8」になるってことだね。
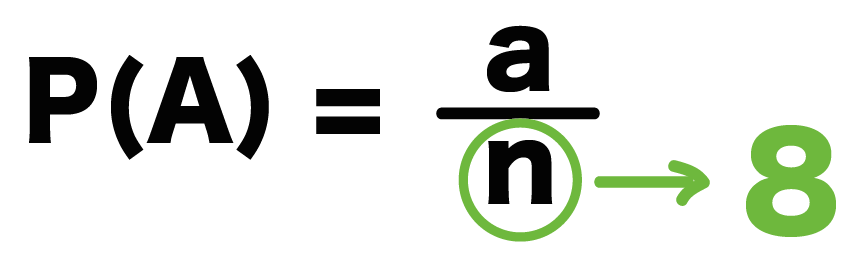
3回とも表がでる場合の数は??
その8通りの中で、
「すべて表」になっているのは何通りなんだろう??
今度はこれを数えていくよ。
樹形図をみると、すべて表なのは1通りだね。
だから、確率の求め方の計算式の「a」は「1」になるね。
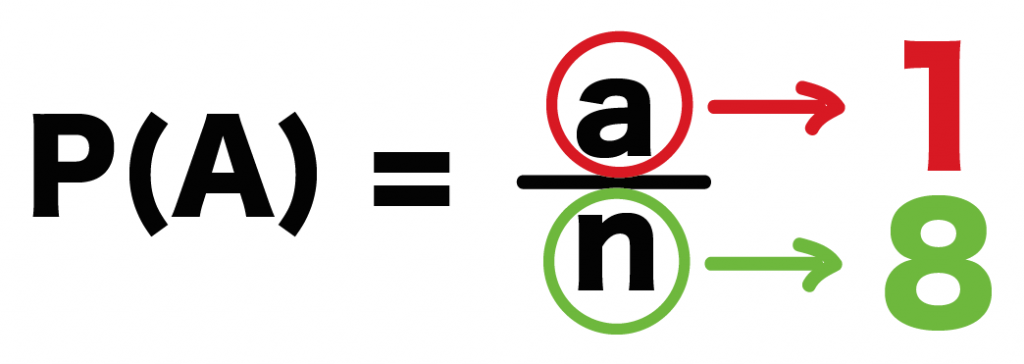
確率の公式で計算してみよう!
あとは公式で計算するだけ。
- すべての場合の数:8
- 表が3回でる場合の数:1
だから、
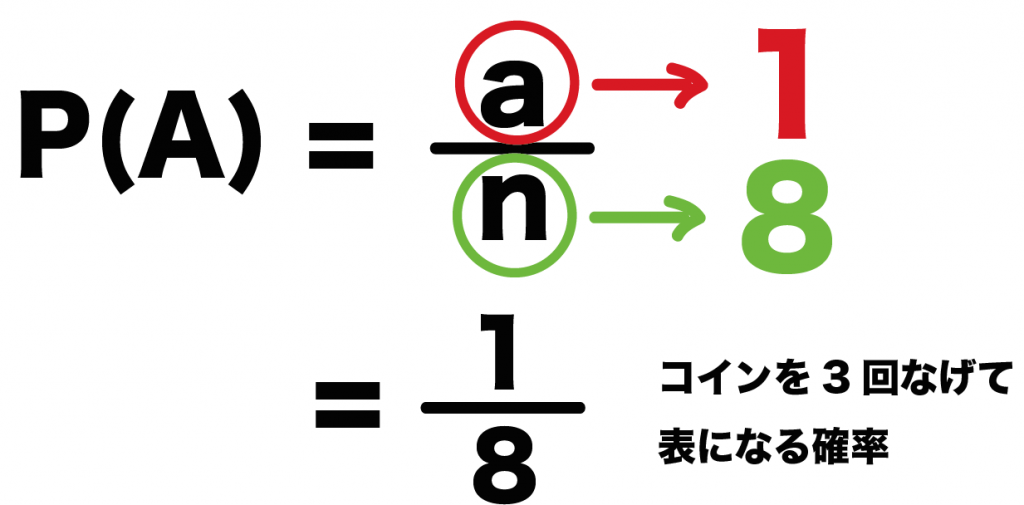
(3回表になる確率)
=(3回表になる場合の数)÷ (3回コインをなげた場合の数)
= 8分の1
になるってわけだ。
おめでとう!
これで確率の求め方の公式がわかったね^^
まとめ:確率の求め方の公式・計算式は1つで十分
中学で勉強する確率の公式は1つ。
P (A) = (ことがらAが起きる場合の数)÷(すべての場合の数)
だけ。
あとは、樹形図で場合の数を正確に数えるだけだ。
問題といて確率になれていこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。






(100-2÷0.03×9)×0.6の求め方がわかりません。回答をお願いいたします。
まずは()の中の掛け算・割り算を計算しよう!
ある体育館の7月の利用者数は,子供と大人を合わせて4500人でした。8月 の利用者数は7月と比べて,子供は30%増加し,大人は20%減少して,大人が 子供よりも450人多く利用しました。この体育館の8月の子供の利用者数は何人 ですか。
求め方を教えて下さい
7月の利用者を文字でおくと解きやすいね
ある商品を定価の1割引で売った。その結果、原価の5%にあたる150円の利益を得ることができた。その後、その商品の原価が3割安くなったので、1500円の利益を上げたい。定価は以前よりいくら高くなるか。
「原価の5%にあたる150円の利益を得ることができた」ってことから原価を計算。
そこから定価も出そう。
あとは、3割安くなった原価を出して、1500円の利益が出るような定価を計算してみよう
10人の委員の中から委員長 書記 会計 を1人ずつ選ぶ方法は何通りあるか という問題で公式を使いたいんのですが、どうすればいいかわかりません
>10人の委員の中から委員長 書記 会計 を1人ずつ選ぶ方法は何通りあるか という問題で公式を使いたいんのですが、どうすればいいかわかりません
10人をA, B, C・・・・として、選び方を樹形図かくといいよ
画びょうを投げる実験を500回行ったところ針が上を向いた結果が340回ありました。この画びょうを投げる時針が上を向く確率はどれだけと考えられますか
>画びょうを投げる実験を500回行ったところ針が上を向いた結果が340回ありました。
この画びょうを投げる時針が上を向く確率はどれだけと考えられますか
全てのトライアルの回数500で成功回数340を割ってみて
規則性の問題が簡単に解ける公式はいくつほどありますか?またそれはどのようなものですか?
大、小二つのサイコロを投げる時目の数の和が5以下になる確率
という問題はどんなふうに解けばいいですか??
>規則性の問題が簡単に解ける公式はいくつほどありますか?
規則性の問題には公式はなくて、問題のパターンに慣れるのが一番
>大、小二つのサイコロを投げる時目の数の和が5以下になる確率
という問題はどんなふうに解けばいいですか??
サイコロが2つの問題は表を書いて場合の数を数えていくといいよ。
やり方は「サイコロが2つの問題の解き方」を読んでみて
袋Aの中から同時に2個の玉を取り出したあと、袋Bの中から1個の玉を取り出す。取り出した三つの玉が、赤玉2個、白玉1個である確率を求めなさい。という問題を出来れば詳しく解説して下さい‼
袋Aの中身は[赤、赤、赤、白、白]
袋Bの中身は[赤、白、白]
>袋Aの中から同時に2個の玉を取り出したあと、袋Bの中から1個の玉を取り出す。
取り出した三つの玉が、赤玉2個、白玉1個である確率を求めなさい。という問題を出来れば詳しく解説して下さい‼
袋Aの中身は[赤、赤、赤、白、白]
袋Bの中身は[赤、白、白]
赤玉2個、白玉1個になるパターンは、
「Aから赤が2つ、Bから白が1つ」と「Aから赤が1つ、Bから赤と白が1つずつ」と「Aから赤が1つ白1つ、Bから赤が1つ」の3パターンだね。
それぞれのパターンで確率を計算して足してみよう。
1組52枚のトランプから1枚抜き取り、カードを見てからもとに戻すことを2回行う時、2回ともハートが出る確率がわかりません。
できるだけ早めに解答送ってください。
>1組52枚のトランプから1枚抜き取り、カードを見てからもとに戻すことを2回行う時、2回ともハートが出る確率がわかりません。
ハートが出る確率xハートが出る確率
を計算してみて
赤い玉が8個、青い玉が5個、黄色い玉が7個。同じ袋に入れた場合、青い玉が出てくる確率を教えて下さい。
>赤い玉が8個、青い玉が5個、黄色い玉が7個。同じ袋に入れた場合、青い玉が出てくる確率を教えて下さい。
玉の確率で1つ取り出す時は、
(ある色の玉の個数)÷(全体の玉の個数)で計算できるよ。
詳しくは「玉を取り出す時の確率」を読んでみて
男子3人と女子4人の7人の生徒から2人の選手を抽選で選ぶとき、2人とも男子になる確率
の計算の仕方を教えてください
「0.1.2.3の4枚のカードがある。このカードのうち、3枚を並べて出来る3桁の整数は、全部で何通りあるか求めなさい」という問題で 解説欄に
百の位 十の位 一の位
3 × 3 × 2 =18通り
とあるのですが この式はどういう意味ですか?
>男子3人と女子4人の7人の生徒から2人の選手を抽選で選ぶとき、2人とも男子になる確率
の計算の仕方を教えてください
1人目が7人から3人の男を選ぶ確率と、
2人目が残り6人から2人の男を選ぶ確率をかけてみよう。
求め方は「くじ引きの確率」と一緒だね
1/7で当たるルーレットで、10回ルーレットをして当たりを引く確率は何%ですか?
かなり高いと思うんですけど…
>1/7で当たるルーレットで、10回ルーレットをして当たりを引く確率は何%ですか?
少なくとも1回あたりが出れば良いのかな?
1-(全部ハズレの確率)で計算しよう
>「0.1.2.3の4枚のカードがある。このカードのうち、3枚を並べて出来る3桁の整数は、全部で何通りあるか求めなさい」という問題で 解説欄に
これは100の位に0は来ないってことがポイントかな。
100の位は0を除く3通りしかなくて、次の10の位は残りの数3通り、一の位は残りの数2つの2通りだ
確率のコツを教えてください!!!
>確率のコツを教えてください!!!
やはり問題のパターンになれることかな!
あとは基本の確率の求め方と、場合の数の数え方をマスターしておけばオッケー
どのくらいの確率なのか話し合いたいので、計算方法を教えて下さい。
1ヶ月(30日として)
10人の会社員が希望休を出した場合、
同じ日を選ぶ確率の出し方を教えて下さい。
10人のスタッフがいる中で、Aさんが他の9人と一か月の希望休が一緒になる確率を出したいのですが、教えて下さい。
>1ヶ月(30日として)
10人の会社員が希望休を出した場合、
同じ日を選ぶ確率の出し方を教えて下さい。
10人が全く同じ日ってこと?
それとも、少なくとも1人がかぶるってこと?
>10人のスタッフがいる中で、Aさんが他の9人と一か月の希望休が一緒になる確率を出したいのですが、教えて下さい。
1-Aさんが9人と全く被らない確率
で計算できそうだね。
ありがとう
A B c D を並べ替えるとなんとうりありますか。
>A B c D を並べ替えるとなんとうりありますか
ならべかえるいちを1つの箱だと考えて、
1番左に入るのはA~Dの4通り、次の右の箱には残りの3つ、次の箱は残りの2つ・・・・
って考えていけばわかりやすいね
A.B.Cの3人がある試験に合格する確率がそれぞれ1/4,4/5,1/2であるとき少なくとも2人は合格する確率は?
①9/40 ②17/40 ③29/40 ④31/40 ⑤33/40
全然解けなくて…お願いします!
大小2枚のコインを使った、2人で行うゲームがあります。
ルール
・参加者は、1人で2枚のコインを同時に投げる。参加者1人につき、1回だけ投げる。
・投げた2枚のコインについて、コイン1枚につき、表が出たら2点、裏が出たら1点を得点とする。
・2枚のコインの得点の合計が大きい参加者を勝ちとする。合計が等しい時は引き分けとする。
京子さん、学さんの順でこのゲームを1回だけ行う時
京子さんと学さんが、得点の合計が
ともに2点で引き分ける確率を
求めなさい。が分かりません!
教えてください!!!
>A.B.Cの3人がある試験に合格する確率がそれぞれ1/4,4/5,1/2であるとき少なくとも2人は合格する確率は?
少なくとも2人合格ということは、
1-(全員不合格の確率+Aだけ合格の確率+Bだけ合格の確率+Cだけ合格の確率)
で計算できるね。
詳しくは「少なくともの確率の問題」を読んでみて
>京子さんと学さんが、得点の合計が
ともに2点で引き分ける確率を
求めなさい
得点が2点ってことは、コインが2枚とも裏になるってことだね。
京子さんが2枚とも裏の確率 x まなぶさんが2枚とも裏の確率
で計算してみよう
残ったカードが12345となる確率を求めるにはどうすればいいでしょうか(´・ω・`)
10本のくじの中に、当たりが3本ある。A、B、Cの3人がこの順にこのくじを1回ずつ引く。一度引いたものは戻さないとして、Cが当たりを引く確率を求めよ。
わかりません。教えてください(;▽;)
3人が当たりを引く確率+2人が当たりを引く確率+Cだけが当たりを引く確率
を計算してみよう!
>残ったカードが12345となる確率を求めるにはどうすればいいでしょうか(´・ω・`)
カードを並び替える問題かな?
3人が当たりを引く確率+2人が当たりを引く確率+Cだけが当たりを引く確率
を計算してみよう!
袋の中に、赤玉2個、白玉4個、青玉1個、黄玉3個が入っている。
この袋から玉を1個取り出す時、赤玉または白玉が出る確率
>袋の中に、赤玉2個、白玉4個、青玉1個、黄玉3個が入っている。
この袋から玉を1個取り出す時、赤玉または白玉が出る確率
赤玉が出る確率と、白玉が出る確率を足してやればいいね!
詳しくは「玉の確率の求め方」を読んでみて
78枚あるタロットカードから、10枚ひいて、その10枚のカードの意味で占う占いが好きです。
78枚のうち大アルカナという、重大な意味を持つカードが22枚あります。
この間は、引いた10枚の内、4枚が大アルカナだったので、すごいなと思っていました。
その話を知り合いにしたら、確率で考えると、そのパターンは多いの?少ないものなの?と質問をされ、ただすごいんだとしか答えられませんでした。
確率の計算の仕方が全然わかりません。教えてください。
3人の子供A.B.Cがじゃんけんを1回だけします。ただし、あいこの場合もそこでやめることにします。
あいこになる確率を求めなさい。
は、どう解きますか??教えてください!
>3人の子供A.B.Cがじゃんけんを1回だけします。ただし、あいこの場合もそこでやめることにします。
あいこになる確率を求めなさい。
まずは確率の分母に当たる全体の場合の数を求めよう。
1人ずつそれぞれ3通りの技があるから、それぞれの場合の数をかけると計算できるね。
あいこになるのはそのうち、全員がぐー、ちょき、パーのいずれかをだす3通りしかない
ある括りで10万人に1人の確率の要素を2つ持ち合わせていた場合の計算は(例えば身長と体重など)、10×10で100万人に1人の確率と単純に考えて良いですか?
>ある括りで10万人に1人の確率の要素を2つ持ち合わせていた場合の計算は(例えば身長と体重など)、10×10で100万人に1人の確率と単純に考えて良いですか?
そうだね!
ある中学校で、2年生の中から卒業式の受付係を2人募集したところ、2人の男子A,Bと2人の女子C,Dの計4人の希望者がいた。この4人から、くじ引きで2人を選ぶ時、男子1人と女子1人が選ばれる確率を求めなさい。 てゆ問題に困ってます教えて下さいㅠㅠ
>ある中学校で、2年生の中から卒業式の受付係を2人募集したところ、2人の男子A,Bと2人の女子C,Dの計4人の希望者がいた。この4人から、くじ引きで2人を選ぶ時、男子1人と女子1人が選ばれる確率を求めなさい。
場合の数は、
AC,AD, BC,BDの4通りになりそうだね。あとは4人の中から2人を選ぶ場合の数で割ってやればいいよ〜
AさんとBさんが階段の途中の同じ段にたっています。二人でじゃんけんををし、勝ったら3段上りあいこだったら二人とも一段上り負けたら一段下りるゲームをしました。2回じゃんけんしたとき二人の段の差が四段になる確率を求めなさい。という問題を詳しく教えてください。
AさんとBさんが階段の途中の同じ段に立っています。二人でじゃんけんをし勝ったら3段上りあいこだったら二人とも一段上り負けたら一段下りるゲームをしました。2回じゃんけんをしたとき二人の段の差が四段になる確率を求めなさい。という問題を詳しく教えてください。
>AさんとBさんが階段の途中の同じ段に立っています。二人でじゃんけんをし勝ったら3段上りあいこだったら二人とも一段上り負けたら一段下りるゲームをしました。2回じゃんけんをしたとき二人の段の差が四段になる確率を求めなさい
差が4段になるということは、
どっちかが勝って、あいこが一回
になるはず。このパターンを(Aが勝利、Bが負け)、(Aが負け、Bが勝利)の2つの場合の数を計算して足せば場合の数が出るはず
サイコロ一個と10円玉2枚を同時に投げる。
このとき、サイコロの出た目の数が3の倍数で10円玉2枚ともが表になる確率を求めなさい。なお、サイコロの出る目、10円玉の裏表が出るのは同様に確からしいとする
>サイコロ一個と10円玉2枚を同時に投げる。
このとき、サイコロの出た目の数が3の倍数で10円玉2枚ともが表になる確率を求めなさい。なお、サイコロの出る目、10円玉の裏表が出るのは同様に確からしいとする
サイコロと10円の確率を計算してかけてみよう
一からわかりません
確率の性質について教科書で読んだのですが、
「起こりうる結果が全部でn通りあり、このうち事柄Aが起こる場合がa通りあるとする。この時aの値の範囲は 0≦a≦n」と書いてあるところが理解できません。
これって簡単にまとめるとどういうことですか?
>確率の性質について教科書で読んだのですが、
「起こりうる結果が全部でn通りあり、このうち事柄Aが起こる場合がa通りあるとする。この時aの値の範囲は 0≦a≦n」と書いてあるところが理解できません。
これって簡単にまとめるとどういうことですか?
起こりうるすべての結果のうち、
ある事柄Aが起こる場合の数は起こりうるすべての数より少ないってことだね!
1·2·3·4·5の5枚のカードをよくきって、1枚ずつ3回連続でいく。
その時にできる3けたの整数が350以上になる確率を求めなさい。
この問題なんですけど、どうやって解くのですか?
(公立入試の問題です。)
>1·2·3·4·5の5枚のカードをよくきって、1枚ずつ3回連続でいく。
その時にできる3けたの整数が350以上になる確率を求めなさい。
この問題なんですけど、どうやって解くのですか?
350以上になるパターンは、
1. 百の位が4か5
2. 百の位が3、十の位が5
の2パターンだね。そいつらの場合の数を数えてみよう
女子三人と男子1人のグループからふたり選ぶとき、そのうち一人が男子である確率
この問題なんですけどどうやって解けばいいですか?
>女子三人と男子1人のグループからふたり選ぶとき、そのうち一人が男子である確率
この問題なんですけどどうやって解けばいいですか?
全員が女子である確率を求めて、1から引いてみた方が早そう。
詳しくは「少なくともの確率の求め方」を読んでみて
>友達3人が、全員同じクラスになる確率または、2人が同じクラスになる確率の求め方を教えてください、、(クラスの数は4クラスで、学年の人数は100人くらいだと思います)
>友達3人が、全員同じクラスになる確率または、2人が同じクラスになる確率の求め方を教えてください、、(クラスの数は4クラスで、学年の人数は100人くらいだと思います)
全員別々のクラスになる確率を計算して、そいつを1から引くといいよ
50%の確率を成功させた上で 30%の確率へ挑み成功させ 更に10%の確率へ挑み成功させる。こういった段階式の最終成功確率はどう求めれば良いのでしょうか?
3つの確立をかけてやればいいよ!
1.2.3.4.5の5枚のカードをよくきって、1枚ずつ3回続けてひき、ひいた順に左から右に並べて3けたの整数をaとする。aの一の位の数と百の位の数を入れかえてできる整数をbとするとき、a-bの値が100以上になる確率を求めなさい。の問題を教えてください!
>1.2.3.4.5の5枚のカードをよくきって、1枚ずつ3回続けてひき、ひいた順に左から右に並べて3けたの整数をaとする。aの一の位の数と百の位の数を入れかえてできる整数をbとするとき、a-bの値が100以上になる確率を求めなさい
これはむずい!が、多分地道にコツコツ場合の数を数えて行くしかないんだろうなあ
大小2個のサイコロを同時に振るときでるめの積が偶数となる確率は
大小2個のサイコロを同時に振るとき2個とも3の倍数がでる確率は
サイコロ2個の確率は表をかいて
場合の数を数えるといいよ
18人の人が勝ち抜くじゃんけん大会で18人づつ5回勝ちぬける確率
2つのサイコロを同時に投げるとき、出る目の数の積が1けたの数である確率はいくらか。
1から6までのどの目が出ることも同様に確からしいとする。
この問題が、分かりません。考え方を教えて下さい。
サイコロ2つの問題は表をかくといいよ!
野球の試合で同点の時、抽選で勝ち負け決めるんだけど、やり方は、18枚の札の内9枚が〇で9枚が✕ AチームBチームが交互に札を引いて〇の多いほうが勝ち 大体5対4で決まるんだけど、たまに6対3があります。9体0になる確率の求め方教えてください。。
赤玉学が二個、白玉が三個、黄玉が二個袋に入っている。色玉を同時に二つ取り出した時、黄玉が揃う確率を求めなさい。みたいな問題が解けません。どうすればいいでしょうか?
式を教えてくださると幸いです
1から15までの自然数を1つずつ記入した15枚のカードがあります。カードに書かれていた数字が2の倍数または3の倍数になる確率を求めなさい。ただし、どのカードを引くときも同様に確からしいものとします。という問題はどうやって解けばいいですか?