【中学数学】正の約数の個数の求め方がわかる3ステップ

正の約数の個数の求め方を知りたい！？

こんにちは！この記事をかいてるKenだよ。植物は癒しだね。

正の約数の個数を求めたい。

そんなとき・・あるよね。。

小さい数の約数なら簡単。

たとえば、

• 2の約数：1と2（2個）
• 8の約数：1, 2, 4, 8（4個）
• 20の約数：1, 2, 4, 5, 10, 20 （6個）

みたいなかんじで、がんばれば約数の個数はわかっちゃう。

だけどね。

むちゃでかい自然数の正の約数の個数を求めたいとき。

こいつはそう簡単にうまくいかない。

たとえば、360の約数の個数を求める問題。

1, 2, 3, ,,,4, ,5, ,,,, 6,,,,,,12,,,,,

って数えてたら日がくれちゃうね。気合だけじゃのりきれない。

そこで今日は、どんなに大きな数でも使える、

約数の個数の求め方の公式

を紹介するよ。

よかったら参考にしてみて。

正の約数の個数の求め方がわかる3ステップ

正の約数の求め方には公式があるよ。

約数の個数を求めたい自然数をNとしよう。

んで、

N = a^p × b^q × c^r

って素因数分解できたとする。

すると、正の約数の個数は、

(p+1)(q+1)(r+1)

になるんだ。

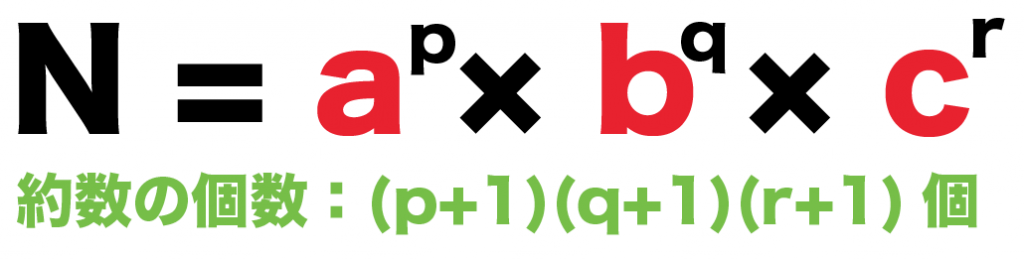
つまり、

（素因数の指数+1）をかけあわせるだけでいいんだ。

たとえば、自然数20の約数の個数を求めてみよう。

こいつを素因数分解すると、

20 = 2^2 × 5

になるね。

正の約数の個数は、（指数＋1）をかけあわせればいいから、

(2+1)×(1+1)
= 6

になるってわけ。

今日はこの公式になれるため、20よりもう少し大きい、

360

の約数の個数をもとめてみよう！

つぎの3ステップで約数の個数を求めることができるよ。

1. 素因数分解する
2. 指数をかぞえる
3. （指数+1）をかけあわせる

Step1. 素因数分解する

自然数を素因数分解してみよう。

360を素因数分解してやると、

• 360÷2 = 180
• 180÷2 = 90
• 90÷2 = 45
• 45÷3 = 15
• 15÷3 = 5
• 5÷5=1

・・っおっと。

1がでてきたのでここでストップだね。

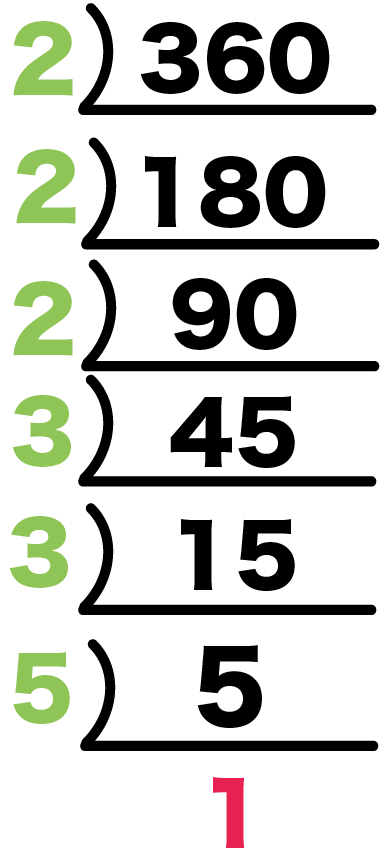
わった素数をあつめて因数にすると、

360 = 2^3 × 3^2 × 5

になるね！

Step2. 指数をかぞえる

つぎは、素因数の指数をかぞえよう。

自然数の360は、

360 = 2^3 × 3^2 × 5

になったね。

素因数の指数に注目してやると、

• 2の指数：3
• 3の指数：2
• 5の指数：1

になってるね。

Step3. （指数+1）をかけあわせる

最後は、

指数に1をたしたもの

を掛け合わせてみよう。

360の素因数の指数はそれぞれ、

• 2の指数：3
• 3の指数：2
• 5の指数：1

だったよね？？

だから、360の正の約数の個数は、

(2の約数の個数+1) × (3の約数の個数) × (5の約数の個数)
= (3+1) × (2+1) × (1+1)
= 24

になる。

つまり、360の正の約数の個数は「24」になるってわけ！

なんで約数の個数が求められるの？？

でもさ、ちょっとあやしくない？？

約数の個数の求め方が、こんなに簡単だなんて・・・

じつは、

「 約数の個数」＝「それぞれの素因数をかけるパターン数」

なんだ。

たとえば、さっきの自然数Nが、

N = a^p × b^q × c^r

に素因数分解できるとしよう。

このとき、素因数aの掛け方の方法は、

• aの0乗
• aの1乗
• aの2乗
• ・・・
• aのp乗

の (p+1)通りあるはず。

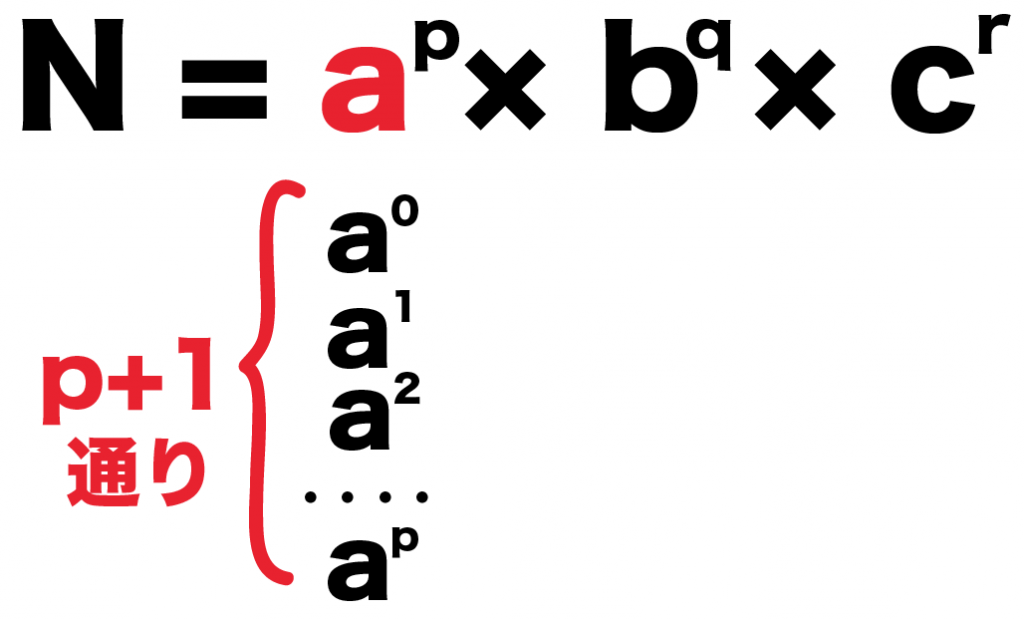
おなじように、他の素因数も考えてやると、

• bの掛け方のパターン： q + 1通り
• cの掛け方のパターン： r + 1 通り

になるはずだ。

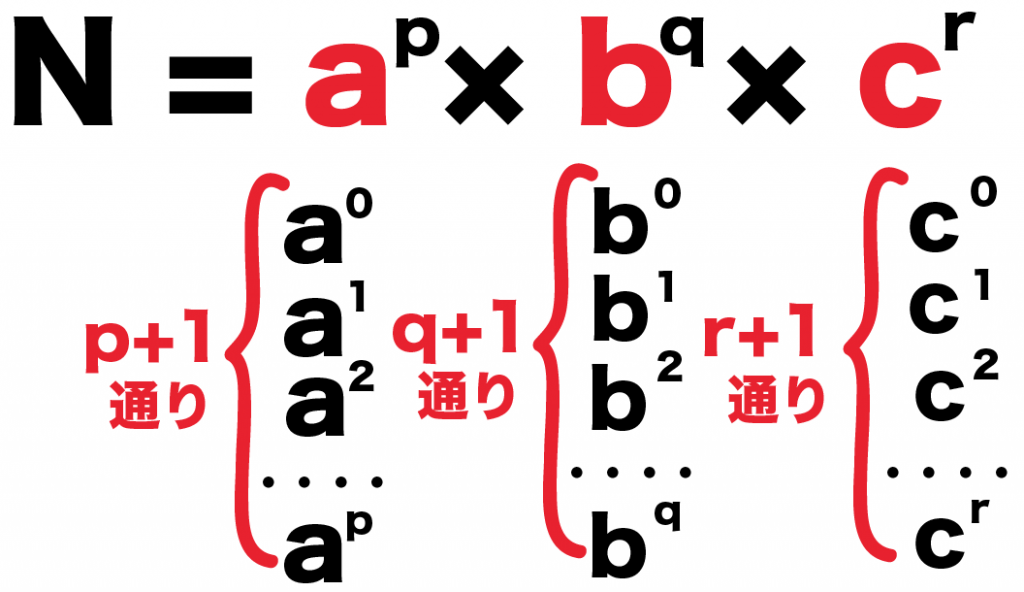
1つの素因数あたりの指数のパターンは、

• p+1 通り
• q+1 通り
• r+1 通り

ある。

だから、自然数Nの約数の個数は、

(p+1)×(q+1)×(r+1)

になるんだ。

どう？？しっくりきたかな？？

まとめ：正の約数の個数の求め方は素因数分解からはじまる！

約数の個数？？

そんなの簡単さ。

素因数分解して、指数に1をたして、かけあわせればいいんだ。

じゃんじゃん素因数分解していこう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。