【中学数学】平行四辺形の高さの2つの求め方

平行四辺形の高さの求め方を知りたい！

こんにちは！この記事をかいているKenだよ。みりんを大人買いしたね。

平行四辺形の高さの問題

ってたまーにでてくる。

たまにね。

「たまーに」なら勉強しなくていいや・・・

と思うかもしれない。

けど、それは大きな間違いだ。

たまーにでるからこそ、

ライバルたちと差がつけやすい問題でもあるんだ！

今日はそんなアツいテンションで、

平行四辺形の高さの求め方

を2つ紹介するよ。

平行四辺形の高さの2つの求め方

高さを求める問題には2パターンある。

1. 「面積」と「1辺の長さ」がわかるヤツ
2. 「内角」と「1辺の長さ」がわかるヤツ

求め方1. 「面積と1辺の長さがわかるとき」

平行四辺形の「面積」と「1辺の長さ」がわかっている問題だ。

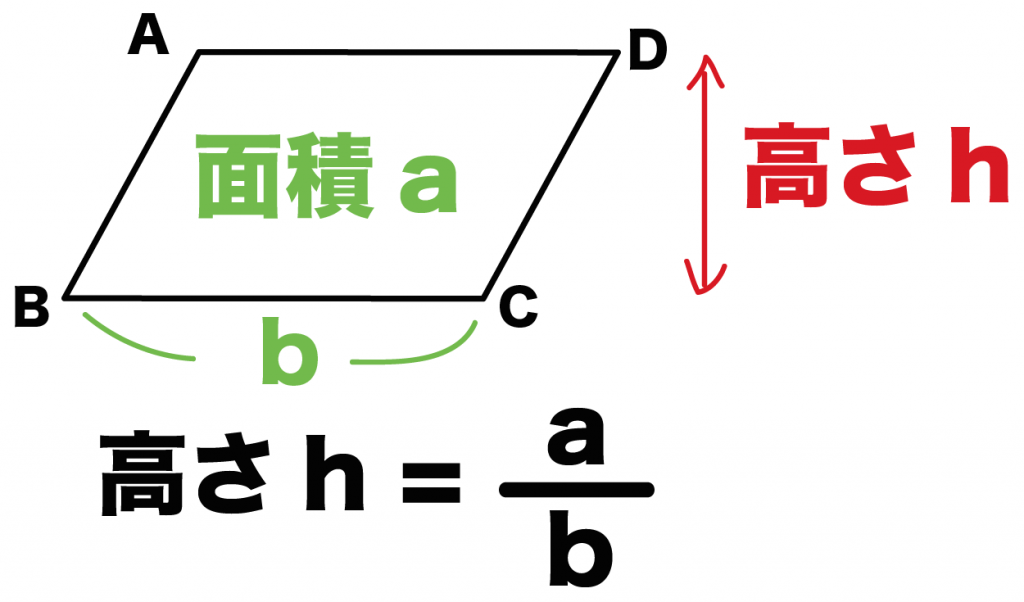
ここでは、平行四辺形の面積の公式を応用してやろう。

面積をa、1辺の長さをbとすると、

高さ = a/b

で求めることができるんだ。

つまり、

（平行四辺形の高さ）＝（面積）÷（1辺の長さ）

ってことだね。

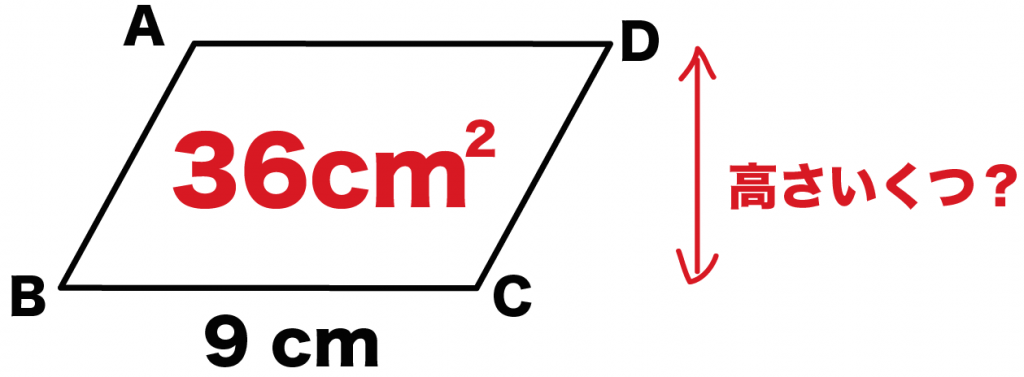
たとえば、面積が36 [cm^2]、BCの長さが9 [cm]の平行四辺形があったとする。

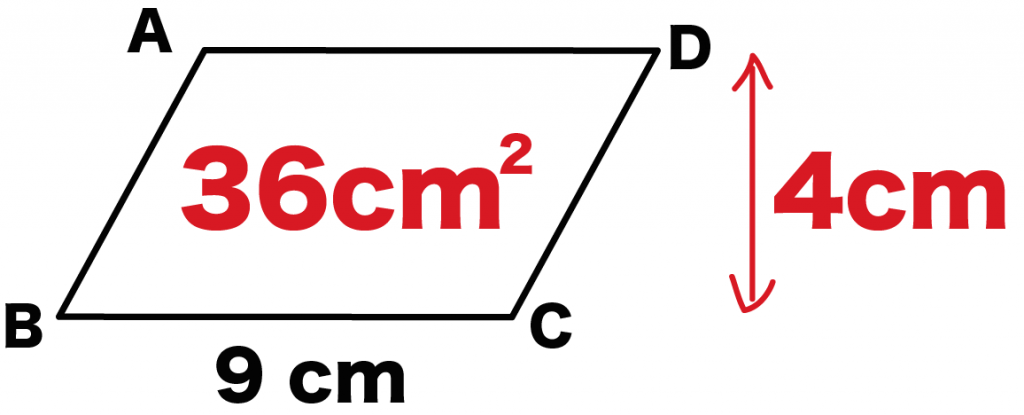
このとき、平行四辺形の高さは、

（高さ）＝（面積）÷（1辺の長さ）
＝　4 [cm]

になるんだ。

このタイプの問題は公式をつかっていこう！

求め方2. 「内角と1辺がわかっているとき」

2つ目は、

「平行四辺形の内角」と「1辺の長さ」がわかってるパターンだ。

この問題では、

直角三角形の比をつかっていくよ。

たとえば、

平行四辺形ABCDのAB = 6 cm、角A = 120°だとしよう。

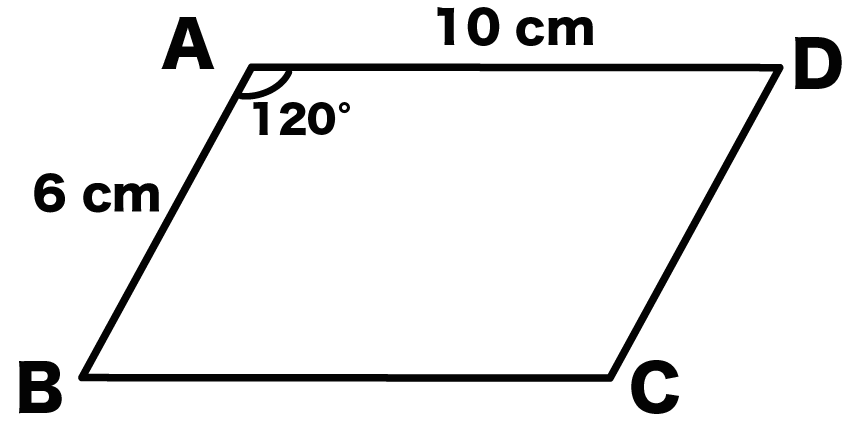
まず、

角度がわかっている頂点から垂線をおろす。

向かい側の辺にね。

平行四辺形ABCDでいうと、

AからBCに垂線をおろすよ。

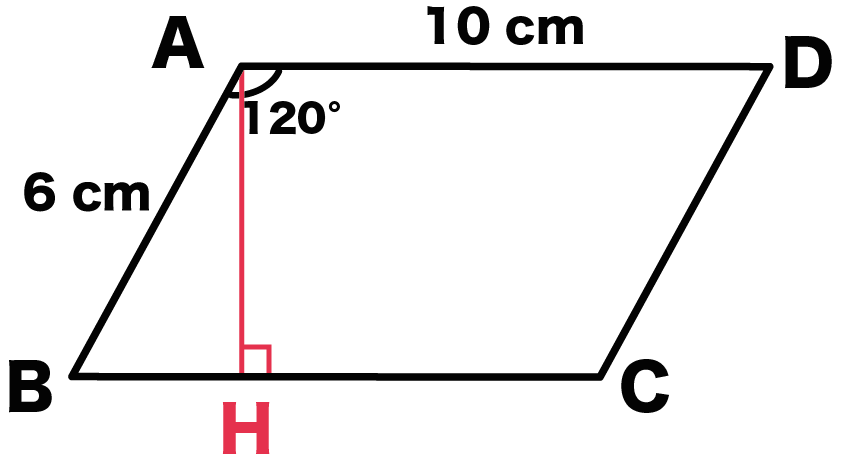
交点をHとしよう。

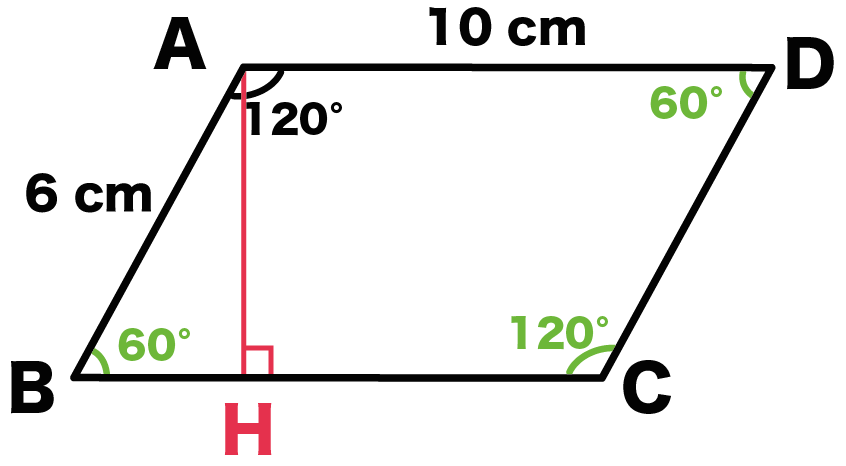
平行四辺形の2組の向かいあう角はそれぞれ等しいから、

• 角A = 角C = 120°
• 角B = 角D = 60°

になるね。

んで、

△ABHに注目してみると、

角60°をふくむ直角三角形になっていることがわかるよね？？

ってことは、

AB : BH : AH = 2 : 1 : √3

になっているはず。

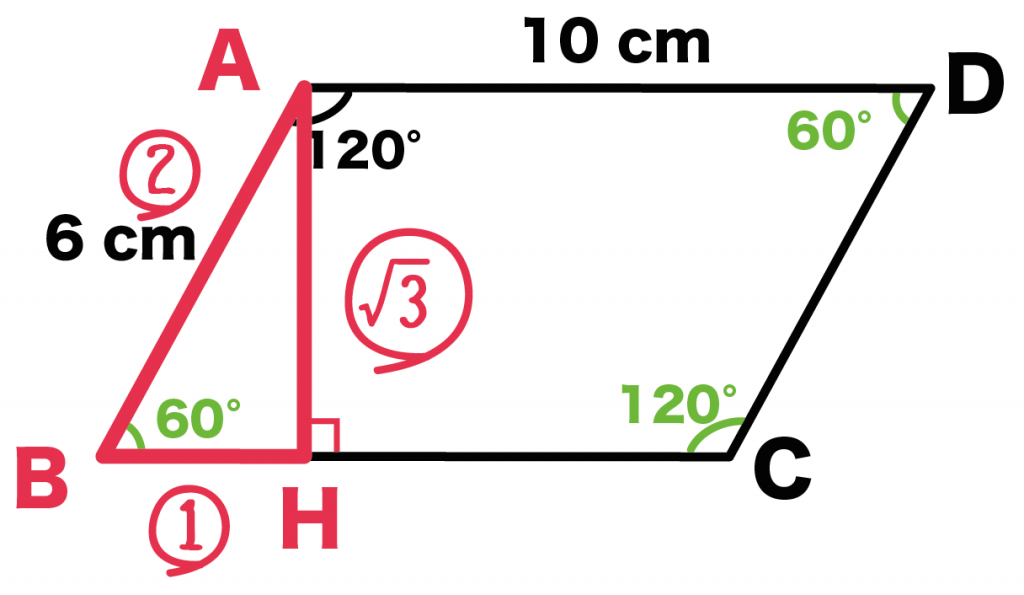
よって、

AH = AB × √3 /2
=  6 × √3/2
=  3√3 [cm]

になるね。

こんな感じで、

垂線をひいて、直角三角形をつくっていこう！！

まとめ：平行四辺形の高さの求め方は2つおぼえとく！

平行四辺形の高さの求め方はシンプル。

1. 「面積」と「1辺の長さ」がわかるとき
2. 「内角」と「1辺の長さ」がわかるとき

の2パターンおぼえておけば、問題ない。

うん、

ガンガン問題をといていこう！

まずは高さがわからない平行四辺形の面積にチャレンジしよう。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。