一次関数と二次関数の交点を求める問題??
こんにちは!この記事をかいてるKenだよ。シロップはやさしいね。
中学数学では二次関数y=ax2を勉強するよね??
二次関数の問題にはたくさんあって、
放物線のグラフをかいたりしていくよ。
なかでも、テストにでやすいのは、
一次関数と二次関数の交点を求める問題
だ。
こんなふうに、
一次関数と二次関数y=ax2が交わっていて、
その交点を求めてね?
って問題なんだ。
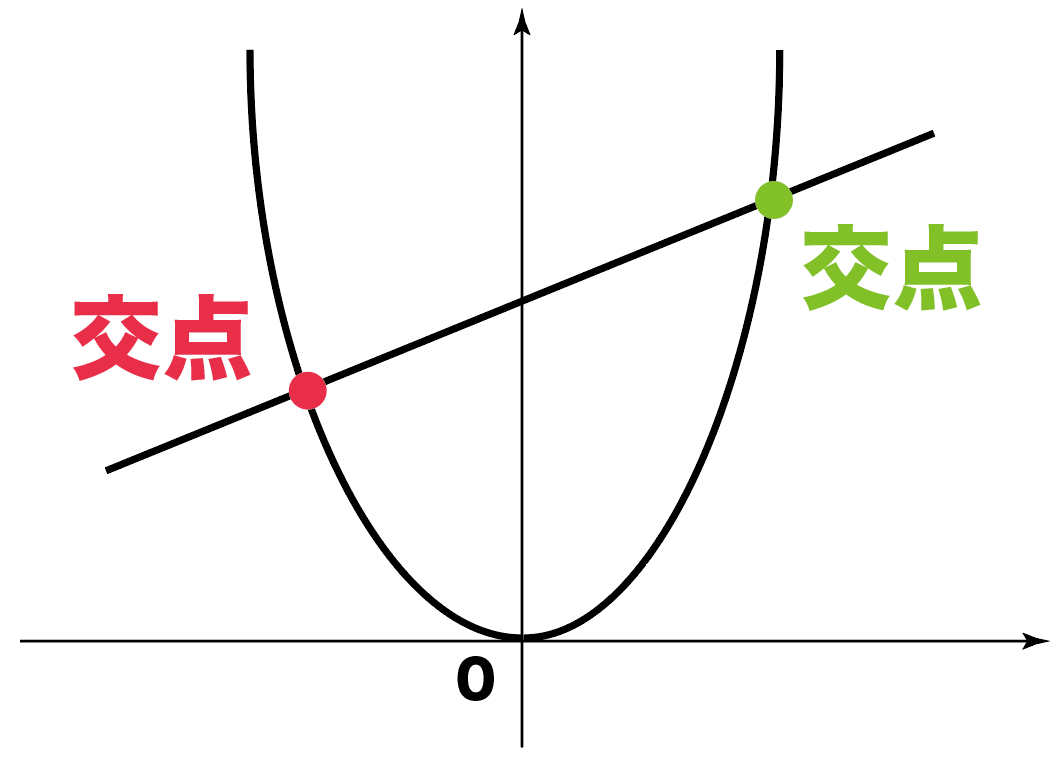
今日はこの問題の解き方をわかりやすく解説していくよ。
よかったら参考にしてみて。
一次関数と二次関数の交点の求め方がわかる4ステップ
さっそく交点をもとめてみよう。
たとえば、つぎの練習問題だね。
—————————————————————————–
練習問題
二次関数 y=x^2 と一次関数 y=x+6 の交点を求めてください。
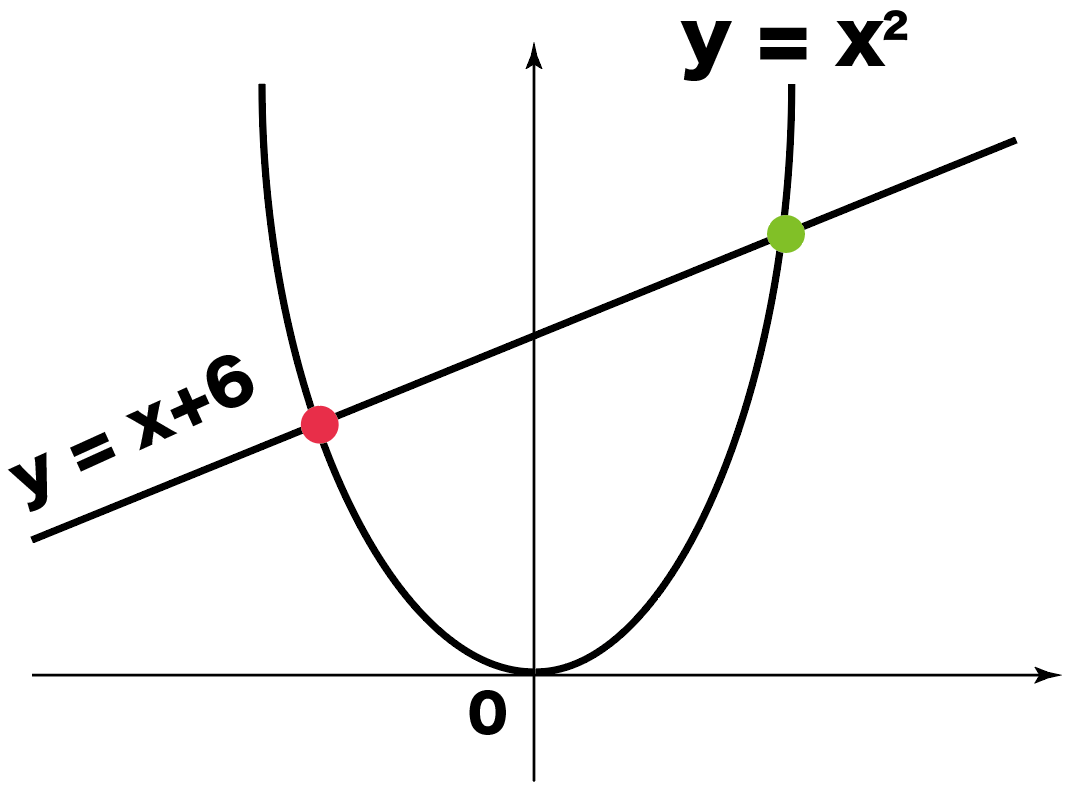
Step1. 連立方程式をつくる
関数の交点を求めるには、
連立方程式をつくるのが一番。
一次関数のときにならった、
2直線の交点の求め方とやり方はおなじだね。
練習問題でも連立方程式をつくってみると、
- y=x2
- y=x+6
こうなるね。
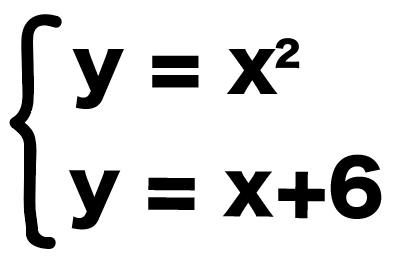
この2つの方程式から、xとyの値を求めていけばいいのさ。
Step2. 連立方程式をとく
さっそく連立方程式をといていこう。
連立方程式の解き方は、
の2つあったよね??
関数の交点を求めるときは、
代入法をつかっていくよ。
なぜなら、
「y =○○」になっていてyが代入しやすいからね。
Step3. 二次方程式をとく
つぎは二次方程式をといていこう。
二次方程式の解き方はたくさんあるけど、
どれをつかっても大丈夫。
練習問題の、
x^2 = x + 6
も解き方はいっしょ。
左辺にぜんぶの項を移項してみると、
x^2 – x – 6 = 0
になるね。
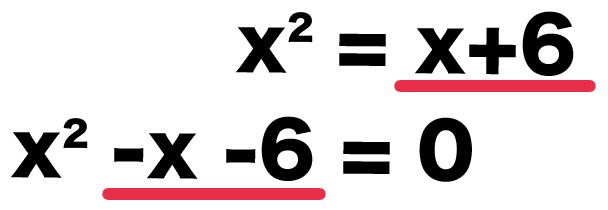
こいつを因数分解すると、
x^2 – x – 6 = 0
(x – 3) (x +2) = 0
になる。
あとは、どっちかが0になっていれば式がなりたつから、
- x – 3 = 0
- x + 2 = 0
この一次方程式をといてやると、
- x = 3
- x = -2
になるね。

Step4. xを関数に代入
最後にxを関数に代入してみよう。
関数にxをいれるとy座標がわかるからね。
2つの交点のx座標が、
- 3
- -2
ってわかったよね??
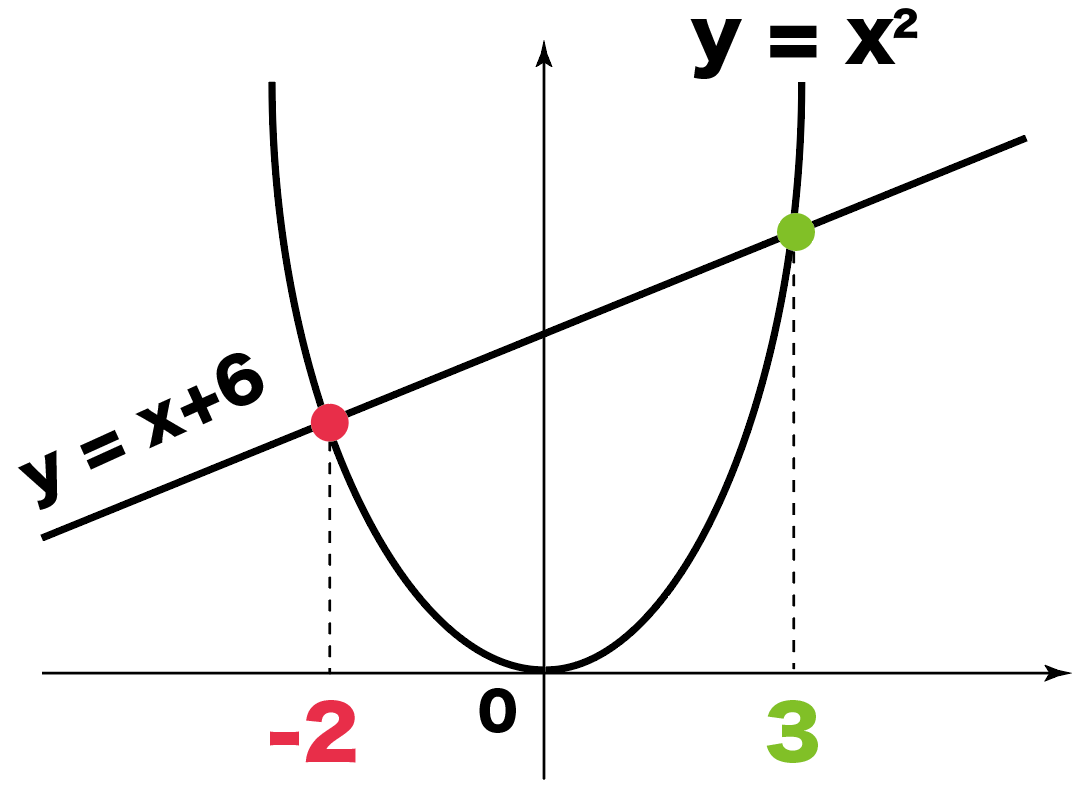
このx座標を、
「二次関数」か「一次関数」
のどっちかに代入するんだ。
今回は、そうだな、
簡単な一次関数「y=x+6」に代入してみよう。
すると、2つの交点のy座標は、
- x = -2のとき、 y = -2 + 6 = 4
- x = 3のとき、y = 3 + 6 = 9
になる。
よって、2つの交点の座標は、
- (-2, 4)
- (3, 9)
の2点になるね。
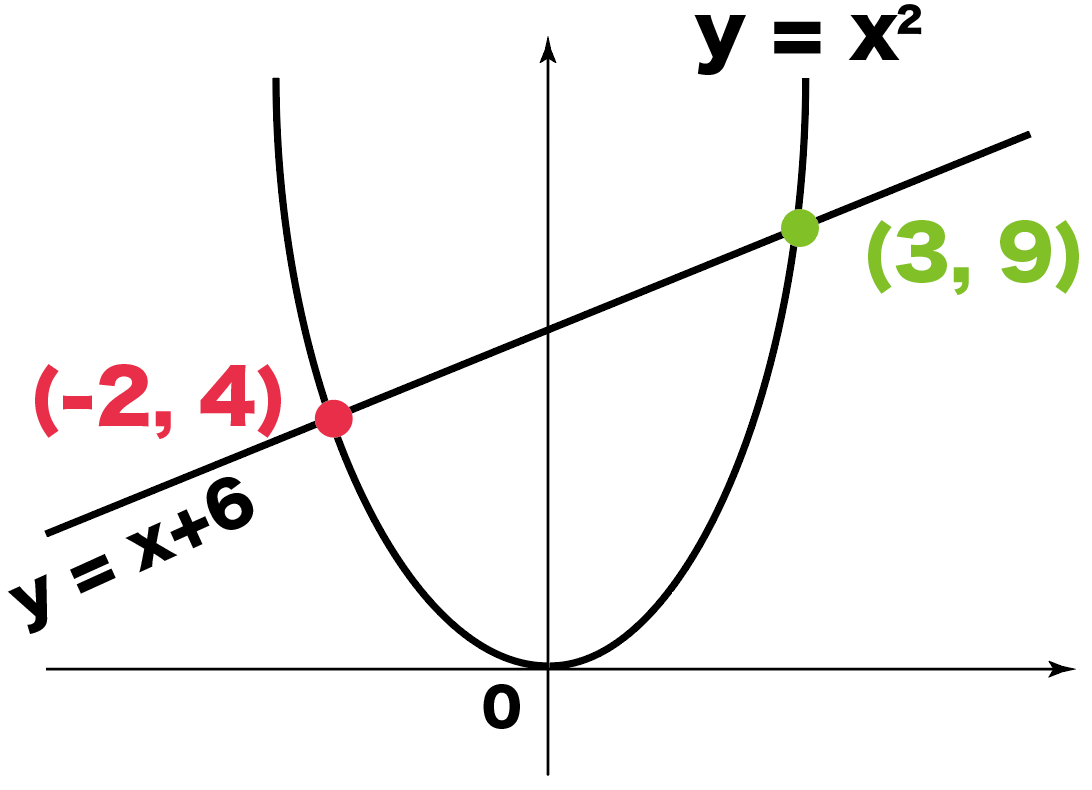
おめでとう!
これで一次関数と二次関数の交点が求められたね。
まとめ:一次関数と二次関数の交点もどんとこい!
一次関数と二次関数の交点を求める問題はよくでてくるよ。
なぜなら、中学数学の総復習になるからね。
テスト前によーく復習しておこうね。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。







y=ax2とy=2x+bが交わっている。 その交点のx座標が-1と5だった。 aとbの値を求めよ
という問題の解き方を教えてください。
まずは2つの式から二次方程式を作ってみよう。
そして、xの座標から因数分解の形を想像して、aとbを出してみよう
こんにちは ありがとうございます
一次関数で、座標(-1・2) と (3・6)を通る直線の長さ、
というのはどうやって求めますか?
お願いします
>一次関数で、座標(-1・2) と (3・6)を通る直線の長さ、
というのはどうやって求めますか?
これは三平方の定理で座標間の距離を出す問題だね。
三角形ABOの面積を半分にする一次関数の求め方を教えて下さい。
>三角形ABOの面積を半分にする一次関数の求め方を教えて下さい。
三角形の位置にもよると思うけど、おそらく、
OとABの中点を通る直線を求めてみよう
xに係数がある場合はどうすればいいのですか?
>xに係数がある場合はどうすればいいのですか?
解き方は同じだよ!
二次方程式を作ってとこうぜ
放物線線上にある
一次関数の式を求める場合、
どうやって求めれば良いですか?
>放物線線上にある
一次関数の式を求める場合、
どうやって求めれば良いですか?
放物線と一次関数の交点がわかってるはず!
その座標を一次関数の式に代入してみよう!
証明の求め方でいつも困るのですが、困らずに正確に溶ける方法はありますか?
>証明の求め方でいつも困るのですが、困らずに正確に溶ける方法はありますか?
証明は言ってることが正しければ正解になるから、必ずしも正確である必要はないよ。
強いていうなら、証明の書き方を使って繰り返し問題をといて、証明の問題自体になれるのがいいね
y=axだとか、xの係数がわからない問題の場合はどうすれば良いのでしょうか。
問題によるかなあ〜
分数で二次方程式を解く際は、どのように整数に直すか教えて下さい!
>分数で二次方程式を解く際は、どのように整数に直すか教えて下さい!
分数はできるだけ、分母を払って消し去ったほうがいいね!
二次関数と一次関数(一次関数はy=2x+kとか)が接しているときは、kと接点の座標をどうもとめればいいですか?
また答えにかいてあるx座標の求め方の、-b/2aはなんでしょうか?軸の方程式な気がするのですが…
>二次関数と一次関数(一次関数はy=2x+kとか)が接しているときは、kと接点の座標をどうもとめればいいですか?
接しているということは、二次関数と一次関数で作る交点の式の二次方程式の解が1つしかないってことだ!
ありがとうございます!
2次関数の式はわかっていて直線の式はわかっていなくてA座標がわかっていてB座標がわかってない場合のB座標はどう求めればいいのですか?
A座標とB座標は直線と曲線は交点です。
>2次関数の式はわかっていて直線の式はわかっていなくてA座標がわかっていてB座標がわかってない場合のB座標はどう求めればいいのですか?
A座標とB座標は直線と曲線は交点です。
Bのxかy座標、一次関数の傾きか切片とか、もう一つ情報が欲しいな
要するにyを抜けば自ずと2次方程式の形になるの?
そうだね!
一次関数の三角形の面積を二等分する直線を求める問題で、中点を出して求める場合とそうでない場合の違いは何ですか。
>一次関数の三角形の面積を二等分する直線を求める問題で、中点を出して求める場合とそうでない場合の違いは何ですか。
三角形のある頂点を通っている直線の場合、向かい側の辺の中点を通ると面積を二等分できる。
がしかし、それ以外の点を通ってる奴らには効かない
x²+x-14=0
ってどうやって解けますか?
教えてください
因数分解で解けなそうだからこれは解の公式が良さそうだな!
y=x2-5x+3
y=0
交点の座標
お願いします
y=0を代入した時のxの値が交点だ!
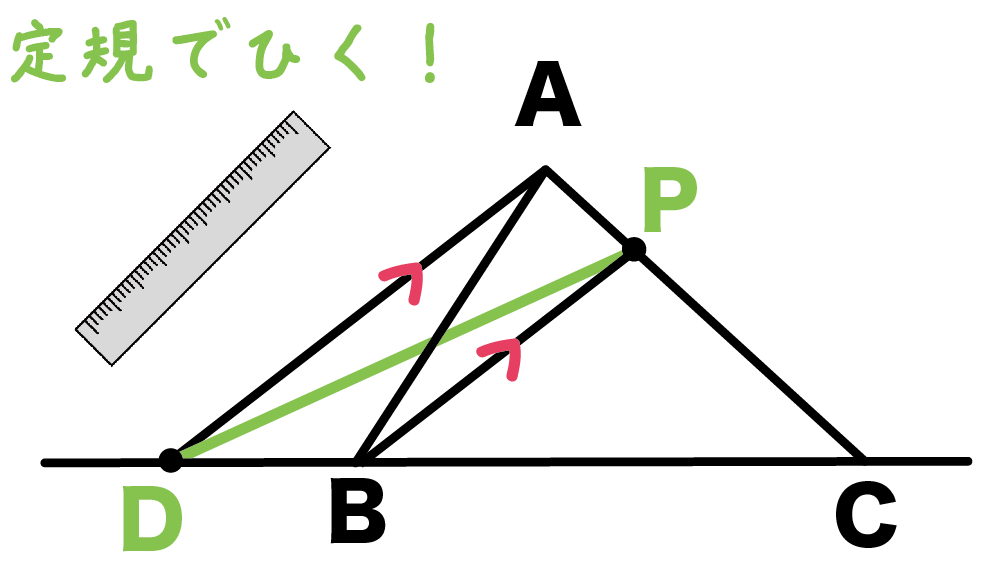
点b(3、9)点c(-2、4)でx軸上に点pを取るときbp+cpが最小になる点pの座標を求めよ。
解き方がわかりませんkenさん教えてください。
これは垂直二等分線を使うだろうな!
y=ーx^2+9xー3 y=3x の2次関数の交点の座標を求めるにはどうしたらいいですか?
正直わかりづらいです。もう少し簡単に説明していただけませんか
一次関数と二次関数の違いって何がありますか?