【中3数学】覚えて損はない！相似な図形の性質2つ

相似な図形の性質ってどんなやつ？？

こんにちは、Drリードだよ。

ここまで相似な図形を勉強してきたよね。

相似の記号もおぼえたし、

相似比も求められるようになった。

今日はね、もう一歩踏み込んで、

相似な図形同士がもつ性質を勉強していこう。

相似な図形たちはどんな性質をもっているんだろう？？

テストで役立つ！2つの相似な図形の性質

さっそく相似な図形の性質を紹介しよう。

つぎの性質があるんだ。

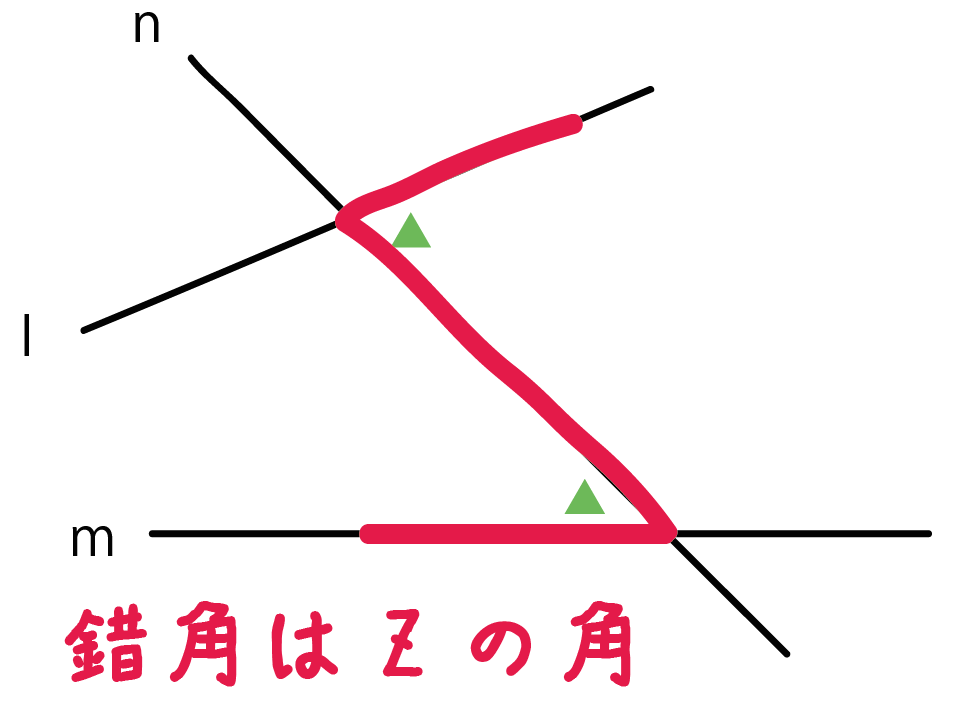
1. 対応する線分の長さの比はすべて等しい
2. 対応する角の大きさはそれぞれ等しい

つぎの△ABCを想像してみて。

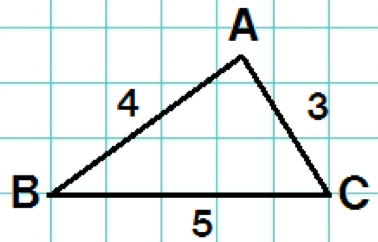
こいつを2倍に拡大してみよう。

スマホやタブレットの画面で、

「ピンチ」して２本指で画面を拡大したことあるよね？

その調子で、△ABCも拡大してみると、

ほれ！

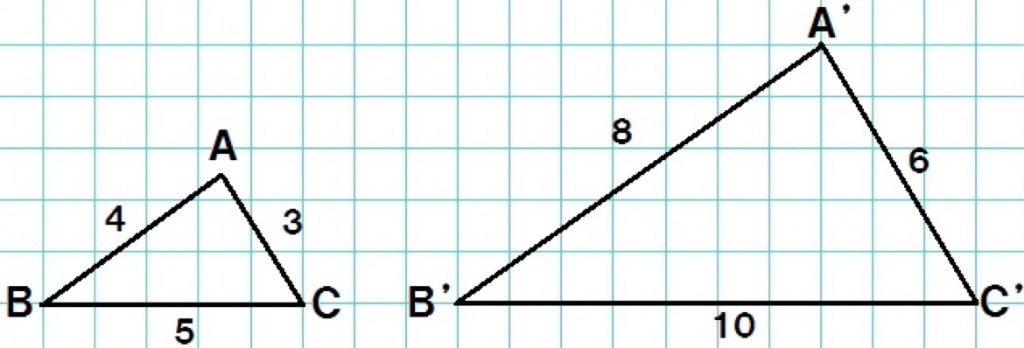
△ABCの2倍の△A’B’C’のできあがりさ。

この2つの三角形をつかって、

相似な図形の性質を確認していこうか。

性質1. 「対応する線分の長さの比はそれぞれ等しい」

相似な図形の性質の1つめは、

対応する線分の長さの比が等しい

ってやつだ。

つまり、ぜんぶの辺の比が同じになってるって性質ね。

それじゃあ、

「△ABC」と「2倍に拡大した△A’B’C’」の、

対応する辺を確認していこう。

対応する辺はそれぞれ、

• ABとA’B’
• BCとB’C’
• ACとA’C’

だね。

色でわけてみたよ↓↓

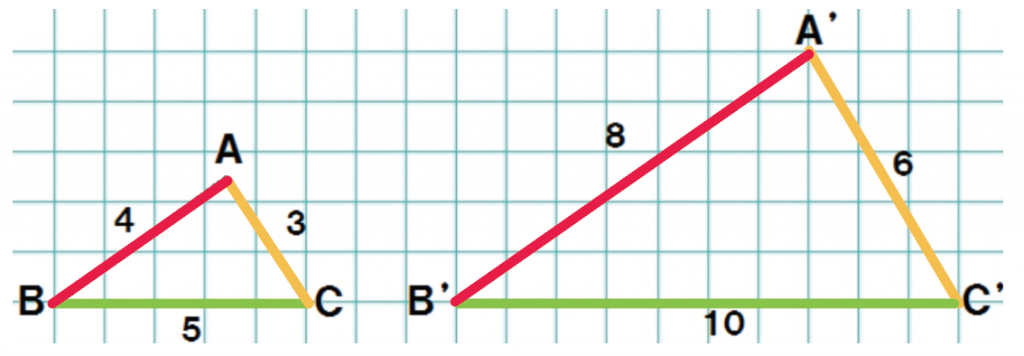
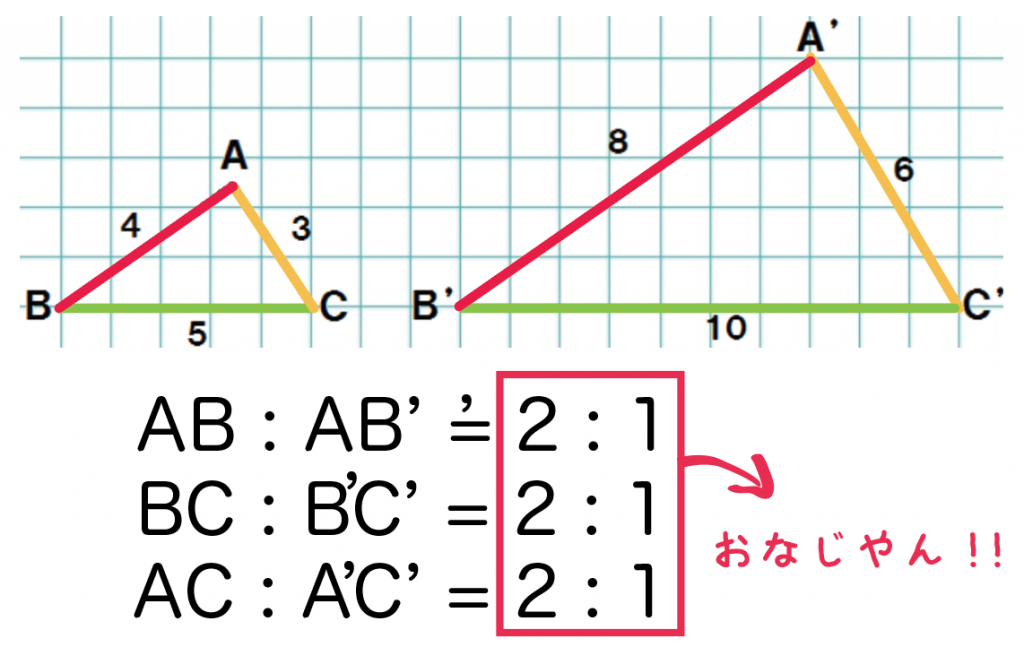
対応する辺の長さについて調べみると、

• A’B’ = 2AB
• B’C’ = 2BC
• C’A’ = 2CA

うんうん、

△A’B’C’ の辺の長さは△ABCの辺の2倍になってるね。

辺の長さの比を書くと、

• A’B’ : AB = 2 : 1
• B’C’ : BC = 2 : 1
• C’A’ : CA = 2 : 1

になってるね。

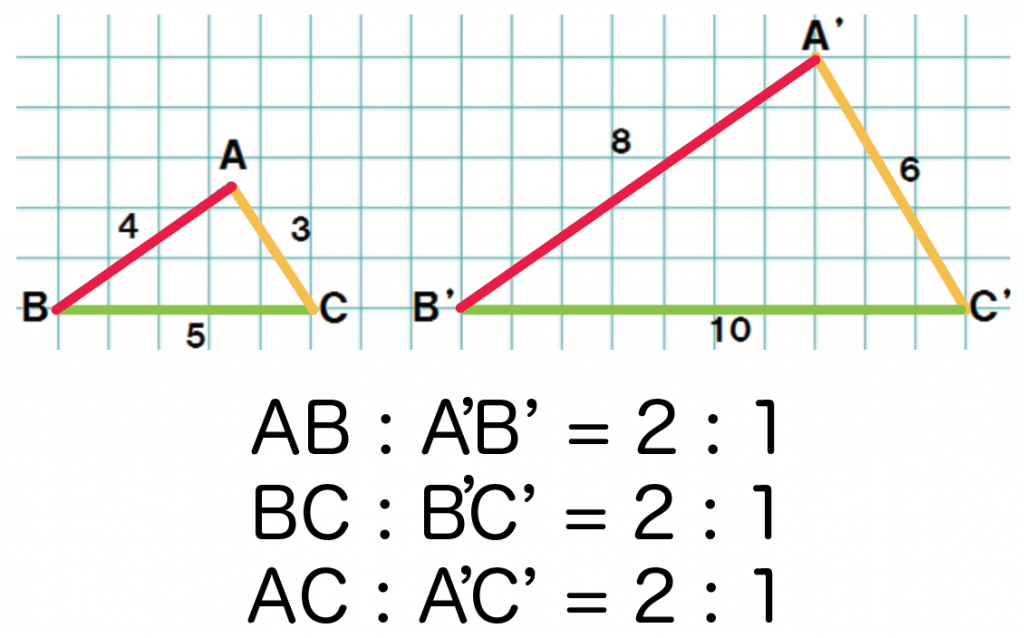
あ！

ぜーんぶの比が2: 1になっとるやん！

ってことは、

対応する辺(線分)の長さの比はすべて等しい

っていえるね。

これが相似な図形の1つめの性質だ。

性質2. 「対応する角の大きさはそれぞれ等しい」

2つめの相似な図形の性質は、

対応する角の大きさが等しい

ってやつね。

簡単にいってやると、

相似な図形の角度はぜんぶ等しいよ！

ってこと。

ためしに、△ABCと△A’B’C’をみてみようか。

実際に分度器で角度をはかってみると、

うわ！

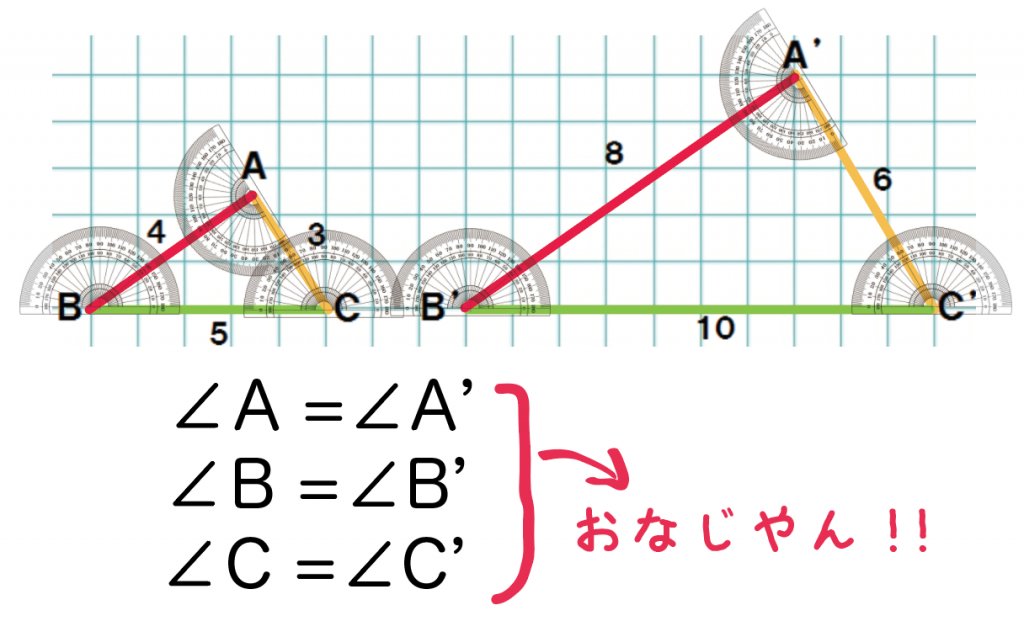
いっしょじゃん！

対応する角たちが等しくなってる！！

• 角A = 角A’
• 角B = 角B’
• 角C = 角C’

えっ。うさんくさいって？？

そういうときは、2つの図形をかさねてみて。

ほら？

きれいに重なるでしょ？

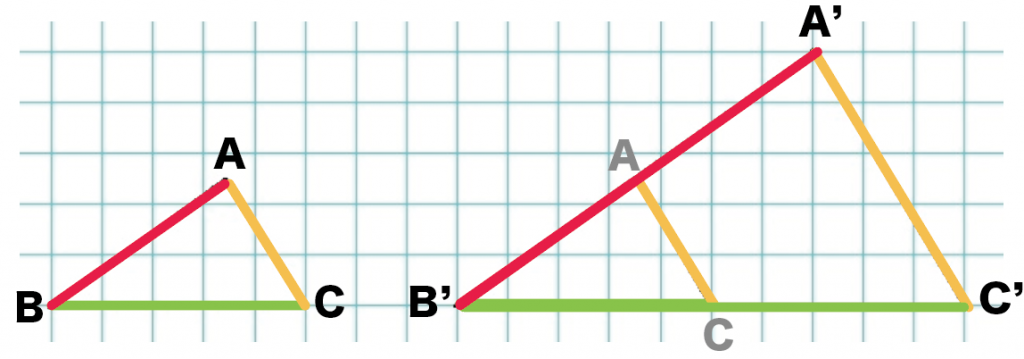
こんなかんじで、

2つの相似な図形の角度は、

ぜーんぶ等しいっていう性質があるんだ！

まとめ：相似な図形の性質は2つだけ！

相似な図形の性質を忘れないように復習しておこう。

相似な図形の性質は、

• 対応する線分の長さの比はすべて等しい
• 対応する角の大きさはそれぞれ等しい

の2つだったね？？

この2つの性質は基本中の基本。

相似な図形を見たときに，

「あ，こことここの角度同じ！」

「相似だから，こことここの比が同じ！」

って気がつくことが大事。

相似の基本的なことだけど、重要だよ。

性質を必ず頭に叩き込んでおこう。

それじゃあ、

Drリード

DR. リード

公立中学校理科数学講師、進学塾数学講師、自宅塾 高校数学英語化学生物指導、国立大学医学部技官という経歴を持つスーパー講師。よろしくな！