【相似の利用】校舎の高さを求める問題の2つの解き方

相似の利用で校舎の高さを求める問題？？

こんにちは！この記事をかいてるKenだよ。肉摂取しすぎたね。

図形と相似の単元では、

相似の利用

を勉強していくよ。

相似を日常でもつかってみよう！

っていう単元。

なかでもよくでてくるのが、

校舎の高さを求める問題

だ。

今日は、この問題のパターンを2つ紹介するよ。

1. 影をつかう問題
2. 縮図をつかう問題

これならどんな校舎がきてもイチコロさ。

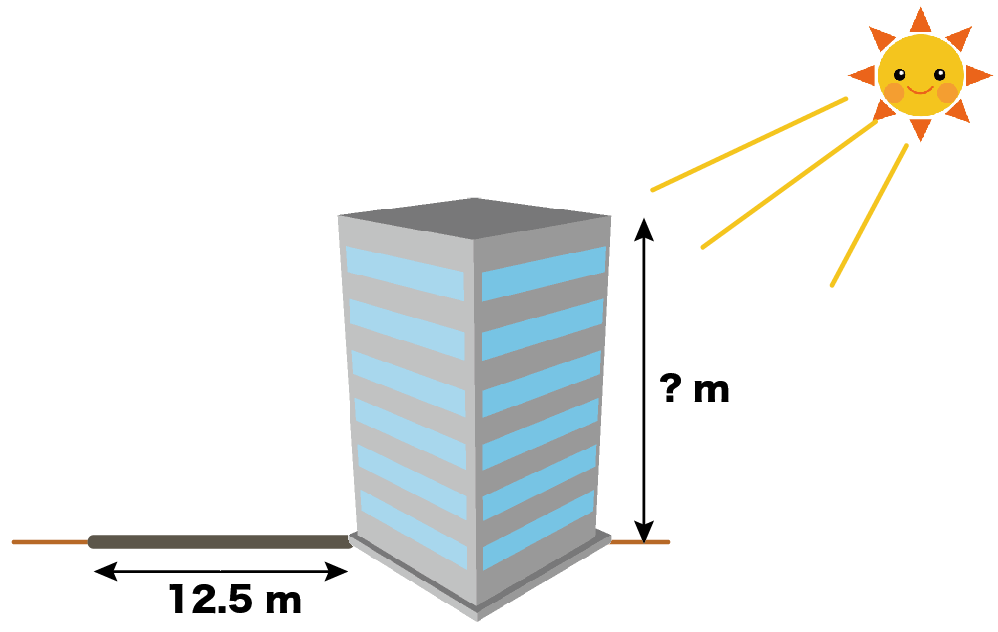
影で校舎の高さを求める相似の利用の問題

まずは、

影で校舎の高さを求める問題を解説していくよ。

つぎの練習問題をといていこう。

天気は晴れ。日中で太陽がでてきます。

身長160cmの人が立っていると0.8cmの影がでてきました。

 

 

いっぽう、校舎の影の長さは12.5 mでした。

 

 

この影をつかって校舎の高さを求めなさい。

この問題は3ステップでとけちゃうよ。

1. 相似な図形をさがす
2. 辺の長さの比を求める
3. 比で校舎の高さをだす

Step1. 相似な図形をさがす

相似な図形をさがしてみよう。

影をつかう問題では、

• 影と人がつくる三角形
• 影と校舎がつくる三角形

の2つが相似になってるよ。

なぜなら、三角形の相似条件の、

2つの角がそれぞれ等しい

にあてはまるからね。

人と校舎は地面に対して垂直にたってるね。

だから、地面と接してる角度は90°。

ある時刻における、

地面と太陽の角度、

つまり、太陽高度はおなじだから、

• 「人の影の先」と「人の頭」がつくる角
• 「ビルの影の先」と「ビルのてっぺん」がつくる角

の2つが等しいはずだね。

だから、

• 影と人がつくる三角形
• 影と校舎がつくる三角形

が相似なんだね^^

Step2. 相似比をだす

つぎは相似比を計算してみよう。

2つの三角形の「影の辺の長さ」に注目してみよう。

それぞれ、

• 人の影 : 0.8 m
• 校舎の影: 12.5 m

だったね？？

2つの三角形の相似比は、

（人の三角形）:（ 校舎の三角形） = 0.8 : 12.5

になるはず。

Step3. 相似比から校舎の高さだす

相似比から校舎の高さを計算してみよう。

校舎の高さをx m とすると、

1.6 : x = 0.8 : 12.5

0.8x = 1.6×12.5

x = 25

になるね。

おめでとう！

校舎の高さゲットできたね。

縮図で校舎の高さを求める相似の利用

おつぎは、

縮図で校舎の高さを求める問題だよ。

これは作図しなきゃいけないから、

• 分度器
• 定規
• コンパス

を用意してね。

つぎの練習問題をといてみよう。

身長1.6mの人間が校舎から20m離れたところから、校舎の頂点をみつめています。

ちょうど校舎のてっぺんが水平方向から42°のところにみえるとします。

 

 

このとき、400分の1の縮図で校舎の高さを計算しなさい。

この手の問題はつぎの3ステップでとけちゃうよ。

1. 縮図をかく
2. 縮図の高さをはかる
3. もとの高さにもどす

Step1. 縮図をかく

まずは、

「人の目」と「校舎」がつくる三角形

に注目しよう。

この三角形の縮図をかけばいいんだ。

問題文では、

400分の1の縮図をつかえ

っていう指示だったね。

「校舎までの距離20m」を400分の1にすると、

5cm。

角度が42°の直角三角形をかいて、その高さをだせばいいってことだね。

まず定規で5cmの直線をかいてあげて、

分度器で42°をはかって直線をひいてみる。

あとは、直角三角形の直角が必要だから垂線をかこう。

コンパスを持ち出す。

そして、5cmのところで半円をかく。

半円と辺の交点にコンパスの針をおき、チョビ円をかく。

逆側の交点にも針をおき、チョビ円をかく。

チョビ円どうしの交点とはじめの半円の中心をむすべば直角のできあがり！

⇒くわしくは垂線のかきかたをよんでね

こんなかんじで、

角度42°の直角三角形の縮図がかけたね。

おそるおそる、直角三角形の高さをはかってみると・・・・

ん！？

4. 5 cm

じゃないか！

Step3. もとの長さにもどす

直角三角形の高さは、

校舎の高さを400分の1に縮めたもの

だ。

400倍して校舎の高さにもどそうか。

実際の校舎の高さ

= 4.5 × 400

= 1800 [cm]

= 18 [m]

になるね。

・・・・おっとあぶねえ。

これは、

人の目線〜校舎のてっぺん

までの距離だ。

「地面」から「人の目線」までの距離

をたさないとね。。

ひとの目線の高さをたしてやると、

18 + 1.6

= 19.6 [m]

になる。

これが校舎の高さだ。

おめでとう！

これで縮図で校舎の高さを求められたね。

まとめ：相似の利用の校舎の高さマスターになった

相似の利用の校舎の問題はどうだったかな？？

校舎の高さを2つの方法で計算できれば大丈夫。

テストに校舎の高さの問題がでても、相似を利用してやればどうにかなるのさ。

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。