【中3数学】2分でわかる！三平方の定理の逆

三平方の定理の逆ってなに？？

やあ、Dr.リードだよ。今日は「逆」だよ。逆。

これまで勉強してきた、三平方の定理には、

三平方の定理（ピタゴラスの定理）の逆

っていうのがあるんだ。

逆は中2数学で習ったやつだったね。

忘れてるやつも多いと思うから、逆を復習しつつ、

三平方の定理でも逆が言えるのか？？

を見ていこう。

=もくじ=

1. 逆の復習
2. 三平方の定理の逆って？
3. 三平方の定理の逆の証明
4. 三平方の定理の逆の問題

中2数学の復習！数学の「逆」ってなに？

まずは数学の「逆」を復習してみよう。

数学の「逆」とはずばり、

ある命題の「仮定」と「結論」を入れ替えたもの

なんだ。

数学の命題とは、「正しいか、正しくないかを考える事柄のこと」だったね。

たとえば、次のような命題があるとするよ。

x =2,  y = 3 ならば x+y = 5

仮定と結論をいれかえて、逆を作ってみると、

x+y = 5 ならば x =2,  y = 3

になるね。

この命題の逆は正しいかな？

「x+y=5」を満たすxとyの組み合わせって「x=2, y = 3」以外にもありそうだよね？

たとえば、「x = 0、 y = 5」とかね。

だから、この場合は逆にすると命題が成り立たないね。

この例みたいに、

ある命題は正しいけど、逆は正しい場合もあるし、正しくない場合も両方あり得るんだ。

じゃあ三平方の定理の逆とは？？

では、三平方の定理の逆はどうだろ。

三平方の定理（ピタゴラスの定理）とはこうだったな。

【三平方の定理（ピタゴラスの定理）】

直角三角形の直角をはさむ２辺の長さをa、b、斜辺の長さをcとすると、

a²＋b² = c²

が成り立つ。

この三平方の定理（ピタゴラスの定理）で逆をつくってみようか。

三平方の定理の仮定と結論は、

• 仮定：「直角三角形である」
• 結論：「a²＋b² = c²」

だ。

この逆をつくってみると、

• 仮定：「a²＋b² = c²」
• 結論：「直角三角形である」

になるね。

つまり、三平方の定理（ピタゴラスの定理）の逆は、

「a²＋b² = c²」ならば「直角三角形である」

だ。

はてさて、これは正しいのかな？

2分でわかる！三平方の定理の逆の証明

三平方の定理の逆の証明してみるか。

わかりきってても、きっちりいくぜぃ。

下の図のような△ABCと△DEFがある。

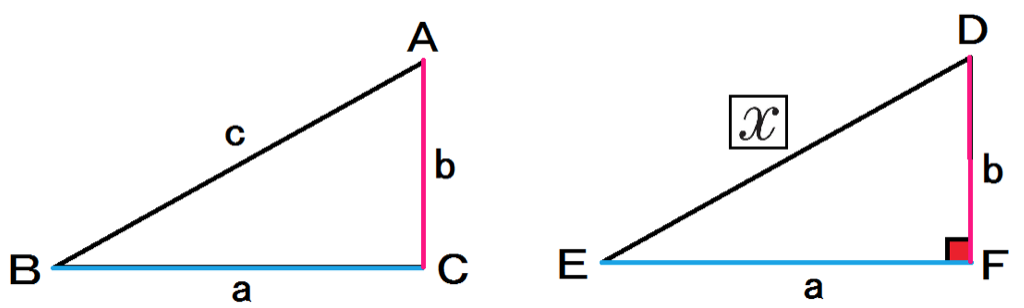
【仮定】

△ABCにおいて　a²＋b² = c²
△DEFは直角三角形である。

【証明】

△ABC と△DEF について、

仮定より、　a²＋b² = c²・・・(1)

△DEFは直角三角形なので　三平方の定理より

a²＋b² = x²   ・・・(2)

 

(1)・(2)より、

c² = x²

c も x も正の数なので 、

c = x

 

△ABCと △DEF の3つの辺がそれぞれ等しいので、

△ABC ≡△DEF

 

よって　∠BCA ＝∠EFD＝90°

したがって、

△ABC は直角三角形である。

この証明からわかるのは、

三平方の定理の逆も正しい！

ってこと。

中学生ならこの証明で十分かな！

三平方の定理の逆をつかった問題を解いてみよう！

三平方の定理の逆をつかった問題を解いてみよう。

2ステップで解けちゃうぜ。

1. 斜辺をどれか確認しておく（一番長いのが斜辺）
2. 「他の2辺の2乗の和」と「斜辺の2乗」が等しいか確認

(1)　3 cm　4 cm  5 cm

一番長い斜辺は5 cmだから、斜辺の2乗は5² = 25。

他の2辺のに乗の和は、

3² + 4² = 25

になるね。

三平方の定理が成り立つから、直角三角形である！

(2)　2 cm　√7 cm　√10 cm

斜辺は√10cmだから、斜辺の2乗は、

(√10)² = 10

になる。

他の2辺の2乗の和は、

2² + (√7)² = 11

三平方の定理が成り立たないから、直角三角形ではない。

(3)  15 cm 13 cm 7 cm

一番長い辺の斜辺は15 cm。

斜辺の2乗は 15² = 225。

他の2編の2乗の和は、

7² + 13² = 218

三平方の定理が成り立たないから直角三角形ではない。

(4) 2 cm 2 cm √6 cm

斜辺は√6 cmだから、斜辺の2乗は、

(√6)² = 6

になる。

他の2辺の2乗の和は、

2² + 2² = 8

三平方の定理が成り立たないから直角三角形ではない。

(5) 2√5 cm  2√6 cm  2√7 cm

斜辺は2√7 cmだ。

斜辺の2乗は(√7)² = 7

他の2辺の2乗の和は、

(2√5)² + (2√6)² = 44

三平方の定理が成り立たないから直角三角形ではない。

(6) 2√5 cm　2√5 cm　2√10 cm

斜辺は2√10 cmだから、斜辺の2乗は (2√10)² = 40になる。

他の2辺の2乗の和は、

(2√5)² + (2√5)²  = 40

三平方の定理が成り立つから、直角三角形。

まとめ：三平方の定理も逆も使いこなせ！

三平方の定理の逆はどうだったかな？

散々「ピタゴラスった！」から慣れたようだね。

つぎは立体で三平方の定理を使えるようになってみよう！

＞＞正四角錐の高さの求め方に挑戦！

それじゃあな！

Dr.リード

DR. リード

公立中学校理科数学講師、進学塾数学講師、自宅塾 高校数学英語化学生物指導、国立大学医学部技官という経歴を持つスーパー講師。よろしくな！