2点を通る直線の式の求め方って??
こんにちは!この記事をかいているKenだよ。焼き肉のたれは便利だね。
一次関数でよくでてくるのは、
二点の直線の式を求める問題だ。
たとえば、つぎのようなヤツ ↓↓
例題
つぎの一次関数の式を求めなさい。
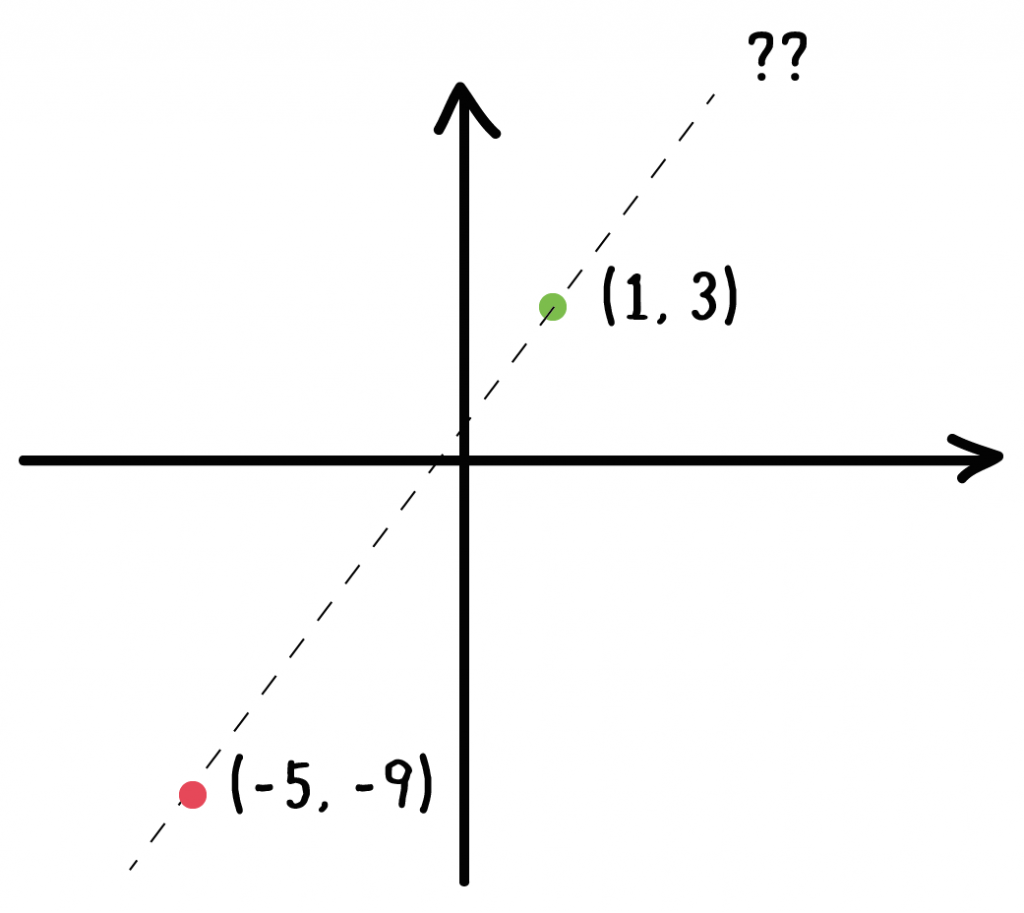
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
今日はこのタイプの問題を攻略するために、
2点を通る直線の式の求め方
を3ステップで解説していくよ。
二点を通る直線の式の求め方がわかる3ステップ
二点を通る直線の式を求める問題には、
- 変化の割合から求める方法
- 連立方程式をたてて求める方法
の2つがある。
どっちか迷うかもしれないけれど、
ぼくが中学生のときは断然、
2番目の「連立方程式をてて求める方法」をつかってたんだ。
シンプルでわかりやすかったからね。計算するだけでいいんだもん。
ってことで、
今日は「連立方程式をたてて求める方法」だけを語っていくよー!
さっきの例題、
例題
つぎの一次関数の式を求めなさい。
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
で直線の式を求めていこう!!
Step1. xとyを「一次関数の式」に代入する
2つの点のx座標とy座標を、
1次関数の式「y = ax + b」に代入してみよう。
例題の2つの座標って、
- (1, 3)
- (-5, -9)
だったよね??
このx座標・y座標を「y = ax + b」に代入すればいいんだ。
すると、
- 3 = a + b
- -9 = -5a + b
っていう2つの式がゲットできるはずだ。
Step2. 引き算してbを消去する
2つの式同士を引き算しよう。
「+b」という共通項を消しちまおうってわけ。
連立方程式の加減法の解き方といっしょだね。
例題の、
- 3 = a + b
- -9 = -5a + b
を引き算してやると、
12 = 6a
になるね。
これをaについてとくと、
a = 2
になる。
つまり、
傾き(変化の割合)は「2」になるってことだね^^
Step3. aを代入してbをゲットする
あとは「b(切片)」を求めればゲームセットだ。
さっき求めた「a」を代入してやるだけで、
b(切片)の値がわかるよ。
例題をみてみて。
aの値の「2」を「3 = a+b」に代入してやると、
3 = 2 + b
ってなるでしょ?
これをといてあげると、
b = 1
って切片の値が求まるね。
これで、
- a = 2
- b = 1
っていう2つの値をゲットできた。
ということは、
2点を通る一次関数の式は、
y = 2x + 1
になるのさ。
おめでとう!! これで二点を通る直線の式もマスターしたね^_^
まとめ:二点を通る直線の式は「加減法」で攻めろ!
2点を通る直線の式は、
- 座標を代入
- 計算
- aを代入
の3ステップで大丈夫。
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。

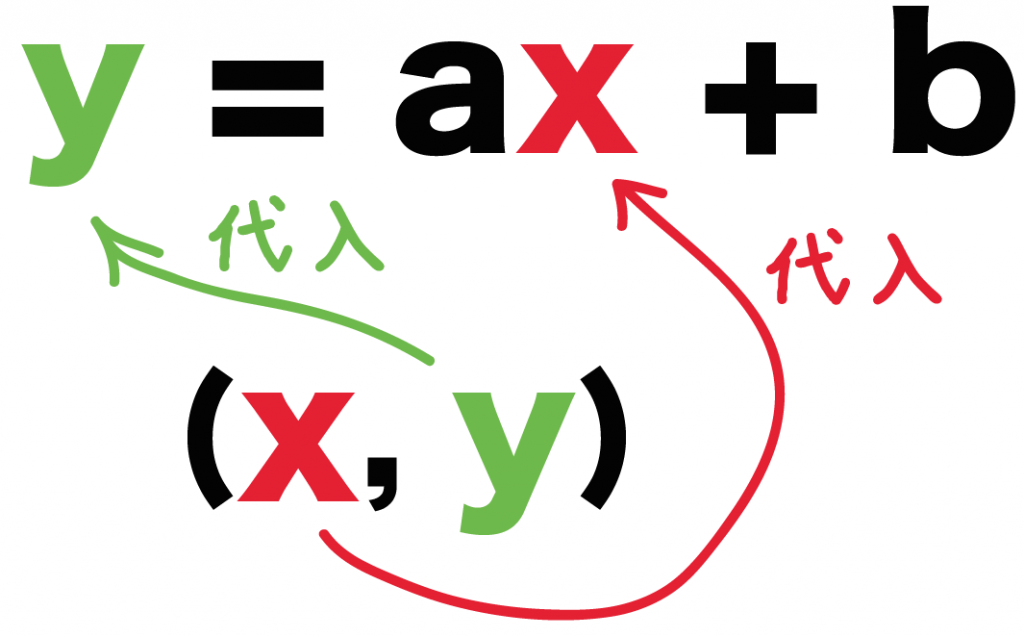





問題で
グラフが直線y=-3x-5に平行で、点(-1,5)を通る。
の、解き方を教えて下さい!
>グラフが直線y=-3x-5に平行で、点(-1,5)を通る。
平行ってことは傾きが等しいってこと。
y=ax+bのaがわかったからあとは座標を代入してbを求めて!
2点を通る直線の式の問題で(3,-5)(-2,-5)のように座標が同じものはどうやって解けばいいですか?
>2点を通る直線の式の問題で(3,-5)(-2,-5)のように座標が同じものはどうやって解けばいいですか?
座標を実際に書いてみるといいよ。
y座標が一定ということは、傾きが0になりそう
2点(0.4)(3.0)を通る直線の式を求めなさい。という問題でも連立方程式で解けますか?
>2点(0.4)(3.0)を通る直線の式を求めなさい。という問題でも連立方程式で解けますか?
解けるよ!
ただ、(0.4)を通るっていう時点で切片が4であることが確定しているから、
y=ax+4に(3,0)を代入してaを出したほうがいいかな
この問題が苦手なので、練習問題で何かやってテストの点数をあげたいのですが、いい問題はありますか?
あったら教えてください!お願いします!
>この問題が苦手なので、練習問題で何かやってテストの点数をあげたいのですが、いい問題はありますか?
あったら教えてください!お願いします!
この問題はまず間違いなくテストにでてくるから押さえておこう!笑
適当に2つの座標を決めて、その直線の式を求める問題を自分で作ってもいいね
まだ解けませんので、お助け下さい。①Y=2/3X+4があり、X軸の切片(6,0)、y軸の切片(0,4)が表示されています。次に①の一次関数に交差し、傾きがわからずY軸の切片(0、-2)の直線がありますが、この直線の一次関数を求めなさい。という設問です。夕べ全く解けずに・・惨敗。求める直線の式をY=ax-2として表示できますが・・どのようにしてaを導き出すのでしょうか?今一度教えてください。できたら急いでいます。勝手言ってすみません。宜しくお願いします。
>①Y=2/3X+4があり、X軸の切片(6,0)、y軸の切片(0,4)が表示されています。
次に①の一次関数に交差し、傾きがわからずY軸の切片(0、-2)の直線がありますが、この直線の一次関数を求めなさい
①の一次関数とどこで交差してる?(交点の座標)
もしくはどうやって交差してる?(垂直、平行など)っていうどちらかの情報がないと解けないかな〜
点(8,0)を通り、2点(-2,2)、(4,5)を通る直線に平行な直線の式を求めなさい。という問題が分かりません。教えて貰ってもいいですか?
>点(8,0)を通り、2点(-2,2)、(4,5)を通る直線に平行な直線の式を求めなさい。という問題が分かりません。
まずは2点(-2,2)、(4,5)を通る直線の直線の式を、連立方程式を解いて計算してみよう。
こいつに平行ってことは傾きが等しいってことだからy=ax+bのaがわかってることになる。
あとはこの式に(8,0)を代入してbを求めたらいっちょあがりだ
2点(5,-6)(-3,2)を結ぶ線分の中点を通りy=3xに平行な直線
という問題が分かりません。教えてください。
グラフが二点(ー1,18)、(2,0)を通る直線である。連立方程式にして解きたいんですが0のときどうなるのかわかりません!
>2点(5,-6)(-3,2)を結ぶ線分の中点を通りy=3xに平行な直線
y=3xに平行ということは、傾きが3で等しいということ。
ってことはy=3x+bであるはずだ。
あとは、2点(5,-6)(-3,2)を結ぶ線分の中点を計算して、その座標をy=3x+bに代入してbを求めよう
>グラフが二点(ー1,18)、(2,0)を通る直線である。連立方程式にして解きたいんですが0のときどうなるのかわかりません!
0の時も同じだよ!
yに0を代入すればいい
簡単な質問で申し訳ないですが‥
(1,2),(5,-6)を通る直線の式を教えて下さい。計算が間違っているのか‥答えが合いません。途中式を含め教えて欲しいです。よろしくお願いします。
2点(-3.4)、(-3.-6 )を通る直線の求め方を教えて下さい!
加減法でしたんですけど、aもbも消えてしまって…
どうすればいいですか?
>(1,2),(5,-6)を通る直線の式を教えて下さい
連立方程式の解き方を使おう。
y=ax+bに2つの座標を代入してaとbの式を2つ作ればいいのさ
>2点(-3.4)、(-3.-6 )を通る直線の求め方を教えて下さい!
これはx座標が一緒のパターンだね。
図をかいてみるとわかるけど、これは特殊なy軸に平行な直線だ
直線x=6と、直線y=x+5および直線y=-4\1x+4との交点をそれぞれA、Bとするとき、線分ABのばぱとら長さを求めよ。
という、問題がわかりません
>直線x=6と、直線y=x+5および直線y=-4\1x+4との交点をそれぞれA、Bとするとき、線分ABのばぱとら長さを求めよ
AとBの座標を計算してみよう!
Aのy座標からBのyの座標を引いたらABの長さが出るぜ
座標上に三角形の図が書いてあり、
辺bc上に点pをとります。(pの座標は分かってる)
三角形abcを二等分する線の式はどうやって求めればいいですか?
>座標上に三角形の図が書いてあり、
辺bc上に点pをとります。(pの座標は分かってる)
三角形abcを二等分する線の式はどうやって求めればいいですか?
条件はPを通るってこと?
そうです…!
条件はPを通るだけ?
もう一点は指定されてないのかな?!
とても分かりやすくて、簡単に解けるようになりました!
5日後に、テストなので頑張ります!
ありがとございました!!
二点(2.7)(6.15)という問題ですが、これも連立方程式で解けますか?
ありがとう!!頑張ろうぜ!!
>二点(2.7)(6.15)という問題ですが、これも連立方程式で解けますか?
解けるよ!
y=ax+bにxとyを代入してaとbの連立方程式を作ってみよう!
とっても分からやすかったです!
変化の割合が2で、2点(1、-1)を通るときの一次関数の式を求めなさいっていう問題なんでが…
解き方を教えてください!お願いします!
>変化の割合が2で、2点(1、-1)を通るときの一次関数の式を求めなさい
変化の割合は一次関数でいうと傾きだったね。
y=ax+bのaのことだから、あとはその式に座標のxとyを入れてbを算出しよう
グラフが2点(-3,1),(2,3)を通る直線の求め方と
その直線の式を求めなさい。
という問題なのですが調べてもどうしてもわかりません。
解き方を教えてください!お願いします
>グラフが2点(-3,1),(2,3)を通る直線の求め方と
その直線の式を求めなさい。
これは連立方程式を作るのが簡単だね。
y=ax+bにxとyを代入して、aとbに関する連立方程式を作って解いてみよう
2点(1.-2)(3.4)を通る直線 の問題が
解けません、、、
連立方程式まで もっていけたんですけど、
なぜか 切片の答えがマイナスなのに
プラスになります 泣
連立方程式が間違ってるだけですかね、?
助けてください!
グラフが点(-2,2)を通り、直線y=x-6とx軸上で交わる。ってどうやってとくんですか?
>2点(1.-2)(3.4)を通る直線 の問題が
解けません、、、
連立方程式まで もっていけたんですけど、
なぜか 切片の答えがマイナスなのに
プラスになります 泣
連立方程式が間違ってるだけですかね、?
作った方程式に求めたaとbを代入して等式が成り立つか確認してみよう!
>グラフが点(-2,2)を通り、直線y=x-6とx軸上で交わる
直線y=x-6がx軸上で交わる点を求めてみよう。
あとはそのx軸との交点と点(-2,2)の2点を通る直線の式を求めればいいね
例えばx=0の時y=-2で、x=4のときy=-6の解き方を教えてください。(連立方程式)
>例えばx=0の時y=-2で、x=4のときy=-6の解き方を教えてください。(連立方程式)
y=ax+bに、2つのxとyのパターンを代入して等式を2つ作ってみよう!
直線L・・y=-2x+14、M・・y=x+5の交点(3.8)とし、L、Mとx軸との交点をそれぞれA(-5.0)、B(7.0)とする。点Pを通り△PABの面積を二等分する直線の式を求めなさい。
という問題を教えてください!
>直線L・・y=-2x+14、M・・y=x+5の交点(3.8)とし、L、Mとx軸との交点をそれぞれA(-5.0)、B(7.0)とする。
点Pを通り△PABの面積を二等分する直線の式を求めなさい。
LとMの交点がPってことかな?
だとすると、PとABの中点を通る直線の式を求めればいいね
2点À2.8B3.11を通る直線の式を教えて下さい
>2点À2.8B3.11を通る直線の式を教えて下さい
y=ax+bに2つの座標を代入して連立方程式を作ってみよう
(6、0)、(6,-2)を通る直線って言う問題が分かりません…教えて下さい。
>(6、0)、(6,-2)を通る直線って言う問題が分かりません…教えて下さい。
y=ax+bに2つの座標を代入してaとbの等式を2つ作ろう。
あとは連立方程式を解くだけ
平面上の3点 A(3,4)B(-1,2)C(k,-3)が同一直線上にあるように、定数kの値を求めなさいという問題で、2-4/-1-3=-3-2/k-(-1)よりk=-11であると書いてあるんですが、なぜこのようにして解けるのかわかりません。教えてください。
>平面上の3点 A(3,4)B(-1,2)C(k,-3)が同一直線上にあるように、定数kの値を求めなさい
まずAとBの2点を通る直線の式を求めてみよう。
そしたらその式にCのy座標を代入して、x座標を求めてみよう!
点(2,-2)を通り,直線y=3x+4に平行な直線を教えて下さい。
>点(2,-2)を通り,直線y=3x+4に平行な直線を教えて下さい。
平行ってことは傾きが等しいってこと。
その直線に(2, -2)を代入して切片を求めてみよう
y=ax²のグラフがあり、そのグラフ上に(3、?)の点Aと(6,?)の点Bがあり、そのABを通る直線は、傾きが3である。aの値を求めよ。
という問題なのですが、全くわからないので教えていただけませんか?
>y=ax²のグラフがあり、そのグラフ上に(3、?)の点Aと(6,?)の点Bがあり、そのABを通る直線は、傾きが3である。aの値を求めよ。
AとBのx座標を二次関数に代入してy座標をそれぞれaで表してみよう。
今度はそのaで表した座標を使って、直線AB(傾きが3)の式に代入して切片bとaに関する連立方程式を解いてみよう
2点(2,0).(0,6)を通る一次関数が分かりません
教えていただけますか?
>2点(2,0).(0,6)を通る一次関数が分かりません
(0,6)を通るってことは切片が6で、y=ax+6になるはず。
あとはそいつに(2,0)代入してaを求めてみよう
2点(5,−6),(−3,2)を結ぶ線分の中点を通り、y=3Xに平行な直線の式を求めよという問題があるのですが、分からないので教えていただければありがたいです。
>2点(5,−6),(−3,2)を結ぶ線分の中点を通り、y=3Xに平行な直線の式を求めよという問題があるのですが、分からないので教えていただければありがたいです。
y=3Xに平行ということは傾きがそいつと等しいってこと。
つまり、y=3x+bになるはずだから、その式に2点の座標を代入してbを求めてみよう
X=-5のとき、x軸と交わり、y=3の時y軸と交わる直線
>X=-5のとき、x軸と交わり、y=3の時y軸と交わる直線
この情報から具体的にどの座標を通るのか考えてみよう!
図にかくとわかりやすいかな
y=2x-5と、
y軸上の+2から
x軸上の+6の地点まで伸びているグラフの
交点はどうすれば求められるのでしょうか。
2x-5=xxxx で求めればいいのは分かるのですが
その式が作れません。教えてください。
「y軸上の+2からx軸上の+6の地点まで伸びているグラフ」の式をまずは求めてみよう。
あとはいつも通り、
y=2x-5と「y軸上の+2からx軸上の+6の地点まで伸びているグラフ」の交点を連立方程式で求めてみよう
分数のときはどうするの?
>分数のときはどうするの?
分数の時も同じだよ〜!
分数を含む連立方程式を解くことになるかな
質問です!
① 点(0.-4)を通りX軸に平行な直線
と
② 2点(-7.6)、(-7.9)を通る直線
という問題を教えてください
2番は両方分数になったのですが計算間違えですよね…?
「2点(-4,1),(2,4)を通る直線の式を求めなさい。」
という問題が分かりません。
連立方程式を立てて求めるのではなく、変化の割合で求めるやり方を教えてください。
>① 点(0.-4)を通りX軸に平行な直線
実際にグラフを書いてみるとわかりやすいかな。
x軸に平行ってことは、xがいくら変化してもyの値が変わらない関数。
つまり、y=定数になるはず
>② 2点(-7.6)、(-7.9)を通る直線
この2つの点はxの値が一緒だよね??
ってことはこの2点を通る直線はy軸に平行な直線になるはず。
実際に書いてみるとわかりやすい
>「2点(-4,1),(2,4)を通る直線の式を求めなさい。」
という問題が分かりません。
連立方程式を立てて求めるのではなく、変化の割合で求めるやり方を教えてください。
yの増加量÷xの増加量で変化の割合が計算できたよね?
ってことで、x、yの増加量をまずは計算してみよう。
詳しくは増加量の計算方法を読んでみて
(0,5) (3,2)を通る問題が意味不明で発狂してたんですが、まじで分かるようになりましたw
感謝です( ´ ▽ ` )
よかった!w
この問題は本当よく出るから解けるようにしておくと楽になるね!
(−1.4)、(2.4a)は、どうやって解けばいいですか?
教えてください。
aが何かにもよるな!
文字としてそのまま扱ってもいいなら傾きとの混同に注意して
連立方程式で問題を解いてみよう
X=0のときy=1,x=1のときy=5となる一次関数の式を求めなさいという問題が、分かりません(๑º口º๑;;)
お願いしますm(*_ _)m
y=ax+bに2パターンのxとyを代入して連立方程式を作ろうぜ!
点(0、4 )を通り、直線y=-2分の1X-1とx軸で交わる。という問題が分かりません教えて下さい。
まずはy=-2分の1X-1 とx軸の交点を求めてみよう!
点p(-3、-1)があり点pをx軸の正の方向にa、y軸の正の方向にbだけ移動したら点(5、-5)と重なった。この時a,bの値を求めなさい。という問題が分からないです。教えてください!
正の方向に移動したってことは、xとyの座標にその移動した分だけ足せばいいな!
(5.-9)(-2.y)のyの出し方を教えて下さい
分かりやっすいけど、焼肉のタレの話がちょっといらない…
(6.3)(−6.0)の直線の式の出し方を教えてください.
とても分かりやすくて参考になりました。ありがとうございます
グラフが2点(−5,−1)(−2,8)を通る直線の式を求める問題の解き方を教えてください♀️
何でa=2を3=a+bに代入するんですか?-9=-5a+bはだめなんですか?
どっちでもいいよ!やりやすいほうで
例えばy=3x +bの場合、
+bの「 +」は「−」に変わることってありますか?
あるある!bに負の数を当てはめたらそうなる!
x=1のときy=3,x=3のときy=5の解き方がわかりません。もしよろしければお教えください。
(3,3)(4,4,)の答えがy=aになったんですけどあっていますか?
2点(3、5)(−3、3)を通る直線と、y=-x+99に平行で(1、−3)を通る直線との交点座標を求めなさい。
解き方がわかりません。 よろしければ教えて頂けないでしょうか。
2点(0.0).(20.10)を通る直線の式をもとめなさい!
という問題の解き方がわかりません。
おしえてくれませんか?
お願いします!
直線 y=4x−3に平行で直線y=x+6とy軸上で交わる直線の式の求め方を教えて下さい