中学数学の因数分解の解き方がよくわからん??
こんにちは!この記事をかいているKenだよ。コーヒーはSに限るね。
因数分解とは何か??ってとこまで勉強してきたね。
だけど、解き方・やり方はピンときてないと思うんだ。
そこで今日は、
中学数学でならう因数分解の解き方・やり方を簡単に解説してみたよ。
よかったら参考にしてみて。
因数分解の簡単な解き方がわかる3つのステップ
因数分解のやり方は3ステップさ。
- 共通因数をくくりだす
- 因数分解の公式を選ぶ
- 公式をつかう
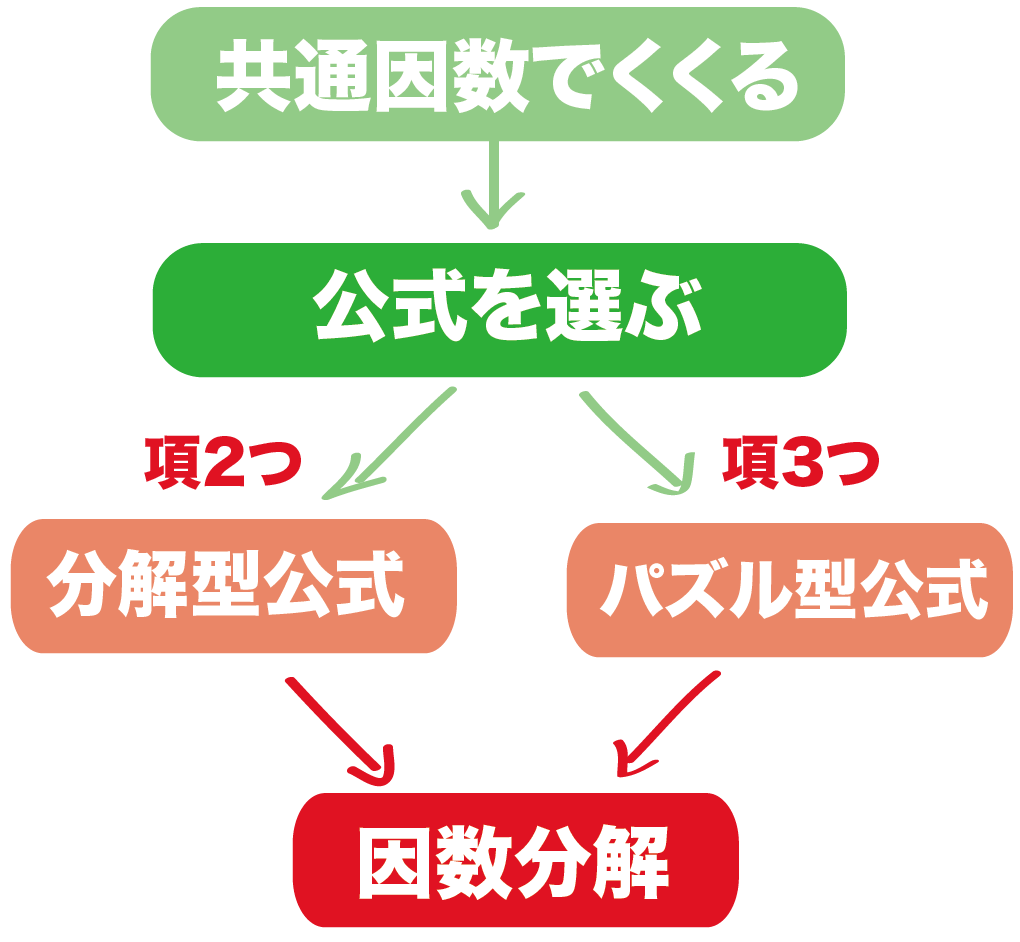
っていわれてもわからんよね??
今日はいっしょに例題をといてみよう。
つぎの多項式を因数分解してください。
5a³ x² + 25a³x -30a³

やり方1. 共通因数をくくりだす
まず共通因数をくくりだすよ。
各項にかかっている同じ因数をくくりだせばいいんだ
⇒くわしい共通因数のくくり方はこちら
例題での共通因数は「5a³」だね。
なぜなら、
すべての項に「5a³」がふくまれているからさ。

共通因数をとりだして()でくくってやると、
5a³ (x² + 5x -6)
になるね!
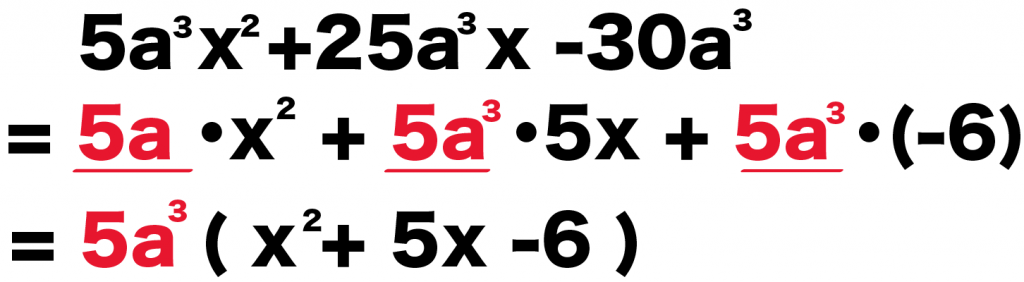
やり方2. 公式をえらぶ!
つぎは因数分解の公式をえらぼう!
中学数学でならう因数分解の公式には、
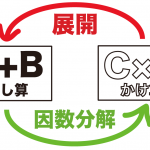
- 分解型
- パズル型
があったよね??
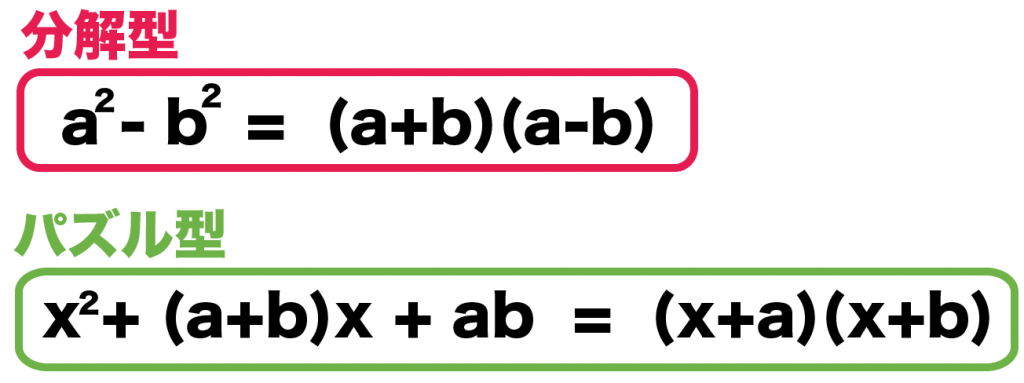
因数分解する「項の数」で公式をえらぶんだ。
- 項の数が「2」⇒ 分解型
- 項の数が「3」⇒ パズル型
ってかんじ。
例題で因数分解したいのは()の中の、
x² + 5x -6
だ。
こいつの項の数は「3」。
だから、パズル型の公式をえらんでみよう!
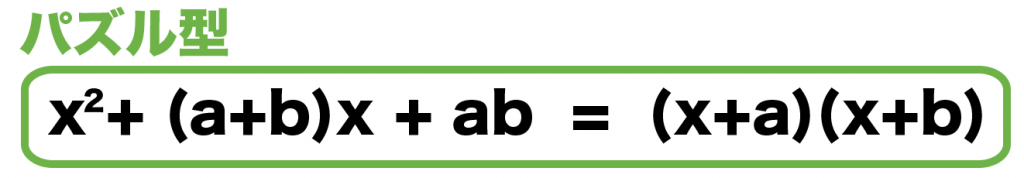
やり方3. 公式をつかう!
公式で因数分解してみよう。
例題では共通因数をだしたあとの、
x² + 5x -6
をパズル型で因数分解するよ。
パズル型では、数・文字のペアーを探すんだったね。
この場合だと、
- かけたら「-6」
- たしたら「5」
になるペアーをさがせばいいよ。

まず、かけ算が-6になるパターンを思い浮かべてみると、
- 1×(-6)
- -1×6
- 2×(-3)
- -2×3
の4パターンある。
そのうち、たしたら5になる組み合わせは、
「-1」と「6」
の1パターンしかないね。
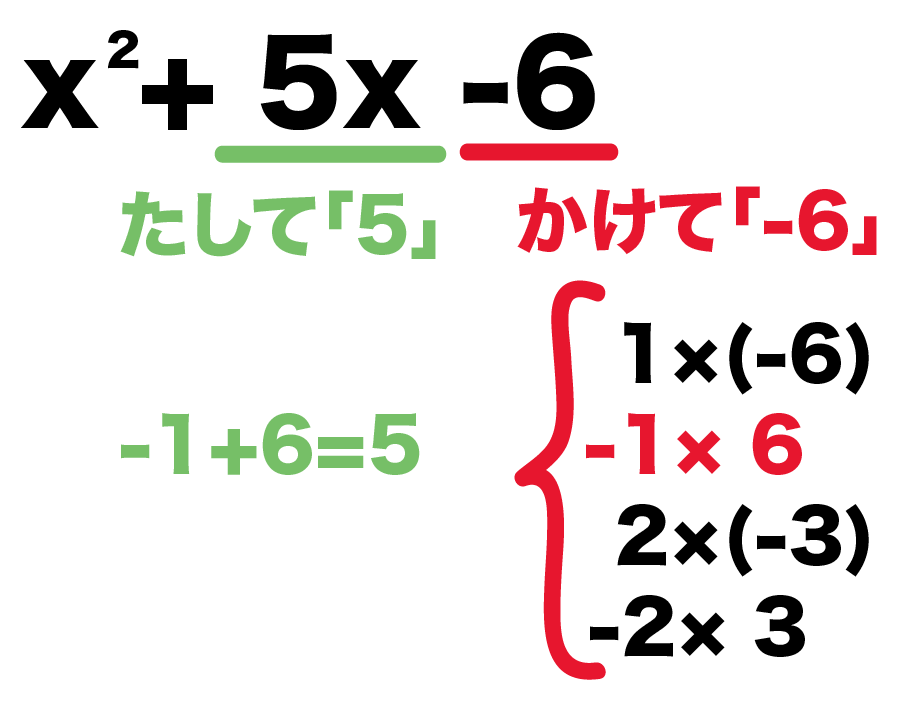
だから、x² + 5x -6 を因数分解すると、
(x-1) (x+6)
になるはずだ。
んで、
くくりだした共通因数をくっつけると、
5a³ (x-1) (x+6)

になる。
おめでとう!
これで因数分解の解き方もマスターだね!
まとめ:因数分解の解き方は公式の選び方できまる!
因数分解の解き方はシンプル。
共通因数をくくりだしてすっきりさせる。
そったら、公式をつかえばいいんだ。
問題をといて慣れていこう!
公式を使った因数分解ができるようになったら、次は置き換えの因数分解の問題にチャレンジしてみよう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。





因数分解の公式が覚えられない。
>因数分解の公式が覚えられない。
公式はひたすら使いまくって覚えるのが一番。
因数分解の公式の覚え方考えてみたから読んでみて
上の問題の場合5a^3はおいておいて、x=1もしくは-6とするのですか?
上の問題は二次方程式じゃなくて因数分解の問題だからxの値は出さなくていいよ!
この問題教えてください!
次の正の約数を、素因数分解を利用して求めなさい。
(1)15
>この問題教えてください!
次の正の約数を、素因数分解を利用して求めなさい。
(1)15
素因数分解してみて、因数を掛け合わしてできる約数のパターンを見つけてみよう
x^2 + 5x -6の項が3というところが理解できませんでした。
kenさんの項にかんする説明を見たのですが+に囲まれたものなのはわかっても
x^2 + 5x -6のどこに3が+で囲まれているのやら・・・
低レベルな質問で申し訳ありません。
>x^2 + 5x -6の項が3というところが理解できませんでした。
kenさんの項にかんする説明を見たのですが+に囲まれたものなのはわかっても
x^2 + 5x -6のどこに3が+で囲まれているのやら・・・
低レベルな質問で申し訳ありません。
項自体が3というわけではなく、項が式に含まれている数が3つってことだね!
項が3なんじゃなくて、3つの項があるってこと!
後二日間の間で出来る効率の良い英語の勉強方
>後二日間の間で出来る効率の良い英語の勉強方
学校の期末テストだったら、本文と新出単語の暗記じゃないかな
項が4個の場合はどうしたら良いのですか?
xy-xz
この問題教えてください
共通因数xで括ろうぜ!