平行線と面積ってどんな単元??
こんにちは!この記事をかいているKenだよ。七味は必須だね。
中2数学では、
平行線と面積
という単元を勉強していくよ。
はじめて「平行線と面積」ってきいても、
えっ、平行線と?
めんせき?
ってなる。
正直よくわからないはずだ。
そこで今日は、
「平行線と面積」で覚えておきたい2つのこと
をかいてみたよ。
予習や復習につかってみてね^^
「平行線と面積」ってぶっちゃけなに??
平行線と面積とはなんだろう??
じつは、これはただの略語なんだ。
なんの略語なのかというと、
「平行線」と「底辺が共通な三角形たちの面積」の性質
だね。

つまり、
「平行線と四角形の面積」のことでもないし、

平行線とただの三角形の面積でもない。

平行線と、底辺が共通な三角形の面積

について勉強していくんだ。
「平行線と面積」で覚えておきたい2つのこと
平行線と、底辺が共通な三角形の面積
で覚えたい2つのことを紹介していくよ。
- 平行線にはさまれた三角形の面積が等しい
- 面積が等しい三角形の頂点を通る直線は平行
平行線にはさまれた三角形の面積が等しい
底辺が共通な三角形では、つぎのことがいえるよ。
平行線にはさまれた三角形同士の面積が等しい
ってね。
たとえば、底辺が共通の△ABCと△DACがあったとしよう。

こいつらが、もし、もしも。
平行線ADとBCにはさまれていたら・・・

△ABC と△ABDの面積は等しくなるんだ。
記号であらわすと、
△ABC =△ABD
になるよ。
たとえば、△ABCの面積が16 [cm^2]で、AB//BCだとしよう。

このとき、2つの△ABC と△ABDは底辺がBCで共通だから、
△ABC = △ABD = 16 [cm^2]
になるってわけ!
すごいよね!
面積が等しい三角形の頂点を通る直線は平行
つぎはさっきの逆だ。
もし、面積が等しい三角形があって、
しかも、
底辺が共通だったとしよう。
このとき、
底辺じゃない頂点をむすんだ直線と、
底辺は平行になっているんだ。
たとえば、
△ABCと△BCDの面積が等しいとしよう。

このとき、
底辺以外の頂点をむすんだ線分ADは、
底辺BCと平行になっているんだ。

つまり、
AD // BC
ってことさ。
なんとなく便利そうだねw
なぜ「平行線と面積」の性質がいえるの??
でもさ、
なんで平行線と面積の性質がつかえちゃうんだろう??
不思議すぎるよね。
じつは、
平行線にはさまれた三角形同士は高さが同じだから
なんだ。

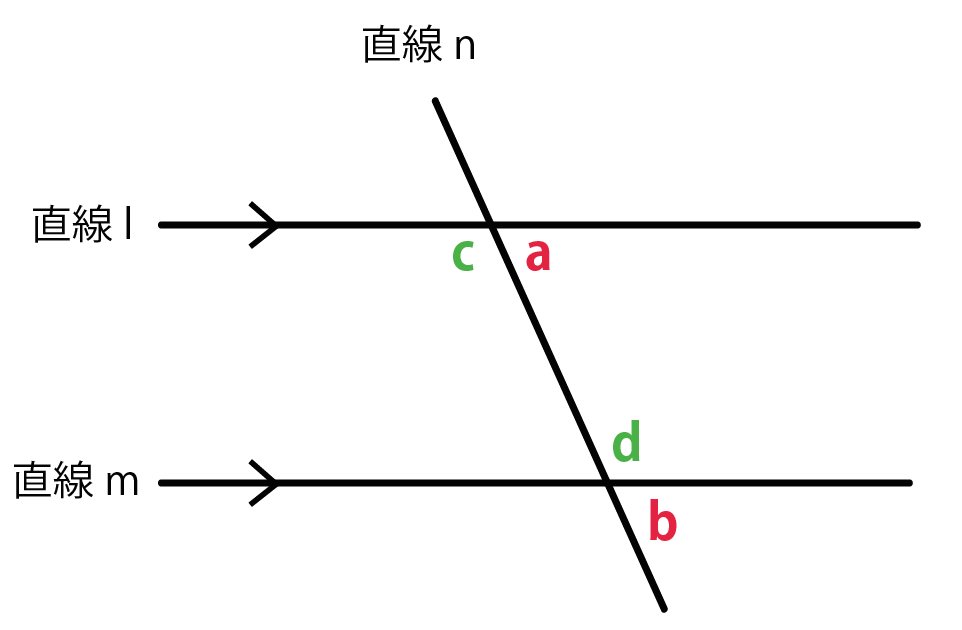
平行な直線って、どーんなに伸ばしまくっても、ぶつからない直線のことだったよね?

ってことは、
平行な直線同士の距離は変わらないってわけさ。

だから、底辺以外の頂点が平行線上にあるとき、
底辺が共通な三角形同士の面積は等しくなるんだ。
だって、
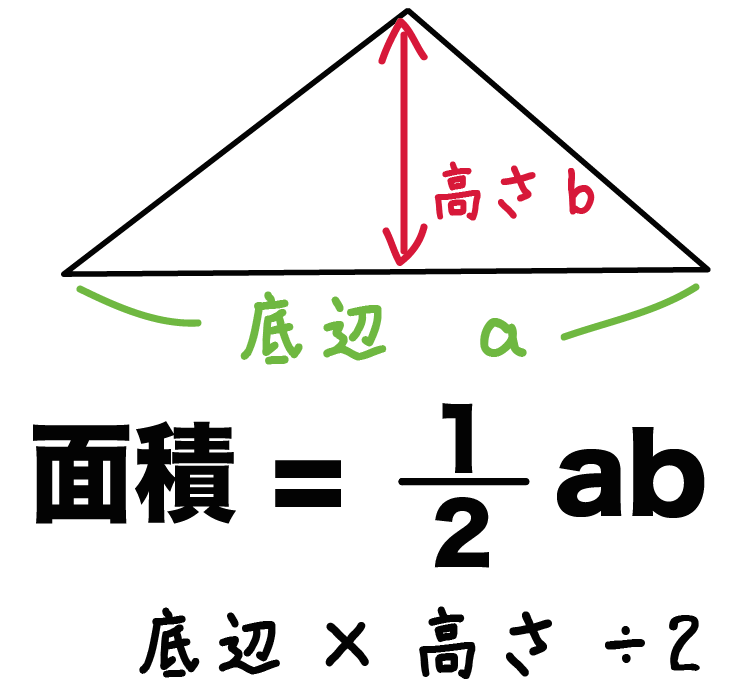
底辺×高さ÷2
のうちの、「底辺」と「高さ」が等しいんだからね。

まとめ:「平行線と面積」は使い方次第!
「平行線と面積」は、
「平行線」と「底辺が共通な三角形たちの面積」の性質
のこと。
これさえおぼえておけば大丈夫。
図形だけじゃなくて、関数の問題でもたまにでてくるから、
しっかり復習しておこう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。




そこから応用問題での、((それを使った応用問題))が全くわかりません。なんか星かたの(平行線ある)図形でそれの中の△ABCと面積の等しいものを選びなさいみたいな問題です。どうすれば出来ますか?
>そこから応用問題での、((それを使った応用問題))が全くわかりません。なんか星かたの(平行線ある)図形でそれの中の△ABCと面積の等しいものを選びなさいみたいな問題です。どうすれば出来ますか?
底辺を共有している三角形っていうのが一つのポイントだ。
そのうち、平行線と面積で面積が等しくなってるやつを見つければいいね。
大抵その手の問題では、
A=B
B=C
よって、
A=c
という感じで三段論法的に等しい三角形を導くことが多いね
境界線の引き直しの書き方
底辺の比と面積の比の求め方がわからないです!
>底辺の比と面積の比の求め方がわからないです!
高さが同じ三角形の時、底辺の長さが面積比になるね!
なぜなら、三角形の面積は底辺と高さで計算するからね
このような問題では、高さが同じでも、同じ面積になるのでしょうか。
あと底辺が同じだとね〜
同じ面積で△ABC=△ADEになるような平行線が使えないときに点D・Eの座標の求め方を教えてください。
点DはX線上で正の数、点EはY軸上、直線DEの傾きは25分の6のときです。