【中学数学】3分でわかる！平方根の近似値の求め方

平方根の近似値の求め方を知りたい！

こんにちは！この記事をかいているKenだよ。血糖値は高いね。

平方根をみていると、

どれくらいの大きさなんだろうな・・？

って思うことあるよね。

ルート！ルート！

っていわれてもデカさわからんし。

たとえば、ある少年に、

19万円ほしい

っていわれたら、大きい金額であるし、慎重になるじゃん？？

でもさ、

ルート19万円ほしい

っていわれてもピンとこないよね？？笑

高いのか低いのか検討もつかん。

今日はそんな事態に備えて、

平方根のだいたいの値の求め方を勉強していこう。

この「だいたいの値」のことを、

数学では「近似値」とよんでいるんだ。

3分でわかる！平方根の近似値の求め方

平方根の近似値を求め方では、

大きな数であてをつけて、じょじょに範囲をせばめていく

っていう手法をつかうよ。

だから、まずは、

その平方根がどの整数の範囲におさまっているのか？？

を調べる必要があるんだ。

さっきでてきた、

√19万円

がだいたい何万円になっているのか？？

を調べていこう！

Step1. 整数で近似値のあてをつける

まずは、

平方根がどの整数と整数の間にあるのか？？

のあてをつけよう。

あての付け方としては、

2乗をしたときに√の中身をこえてしまう整数

と

ギリギリこえない整数

をだせばいいんだ。

√19で考えてみよう。

整数を1から順番に2乗してみると、

• 1の2乗 = 1
• 2の2乗 = 4
• 3の2乗 = 9
• 4の2乗 = 16
• 5の2乗 = 25

・・・・・・・

になるね。

どうやら、「19」は、

• 4の2乗 = 16
• 5の2乗 = 25

のあいだにありそうだね。

よって、√19は、

4 < √19 < 5

の範囲におさまってるはず！

つまり、

√19の1の位は「4」ってわけだね。

ふう！

Step2. 小数第1位をもとめる

近似値の1の位はわかったね？？

おなじことを小数第1位でもやろう。

「√19」の1の位は4だったね？？

今度は、小数第一位の数字を1から順番に大きくしていこう。

んで、

2乗して19をこえるポイントをみつければいいんだ。

• 4.1の2乗 = 16.81
• 4.2の2乗 = 17.64
• 4. 3の2乗 = 18.94
• 4.4の2乗 = 19.36

・・・・

ぬぬ！

19は、どうやら、

• 4.3の2乗
• 4.4の2乗

のあいだにありそうだね。

ってことは、√19の範囲は、

4.3 < √19 < 4.4

になるはずだ。

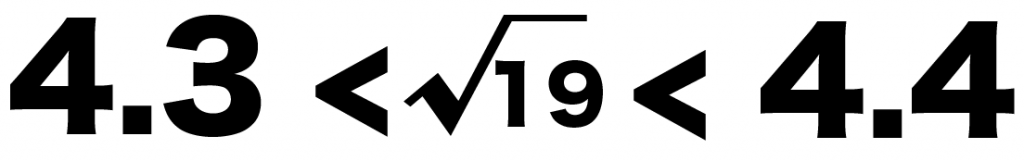
だから、√19の小数第1位は「3」になるはずだね。

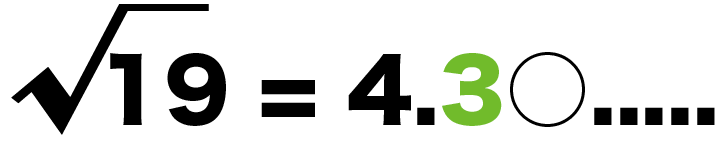
Step3. 小数第2位をもとめる

最後もやり方はおなじ。

小数第2位を1から順番に増やして2乗。

ルートの中身を超えるポイントをみつければいいんだ。

√19でも小数第2位のあてをつけよう！

小数第1位は「3」だったよね？？

だから、調べるのは4.31からだ。

0.01ずつたして、そいつらを2乗していこう！

• 4.31の2乗 = 18.5761
• 4.32の2乗 = 18.6624
• 4. 33の2乗 = 18.7489
• 4.34の2乗 = 18.8356
• 4.35の2乗 = 18.9225
• 4.36の2乗 = 19.0096

おっと！

4.36の2乗で19をこえちゃったね。

ってことは、19は、

• 4.35の2乗
• 4.36の2乗

の間にあるはずなんだ。

つまり、

4.35 <√19 < 4.36

になってるね！

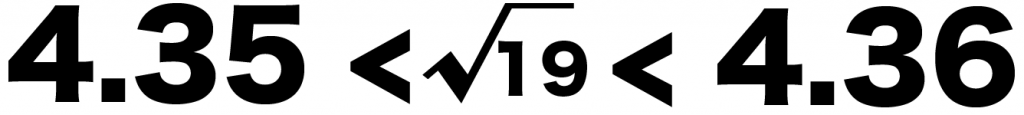
ってことは、

√19の小数第2位は「5」になるはず！

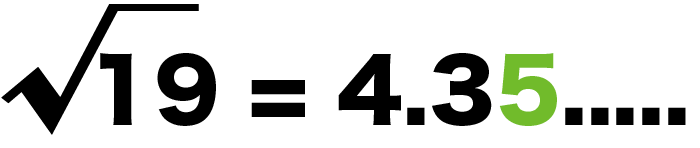
やったね！

この「4.35」が√19の小数第2位の近似値だよ^^

あの少年は4.35万円、つまり、4万3500円ぐらいを請求していただわけだね。

まったく、可愛いけど憎いやつだ。

こんな感じで、

1の位からじょじょに範囲をせばめていこう！

平方根の近似値があってるか確認！

平方根の近似値があってるか確認してみて。

計算機の√ボタンをおしてやれば・・・・ほら！

一発で平方根の近似値がだせるんだ。

たくさんのケタ数をね。

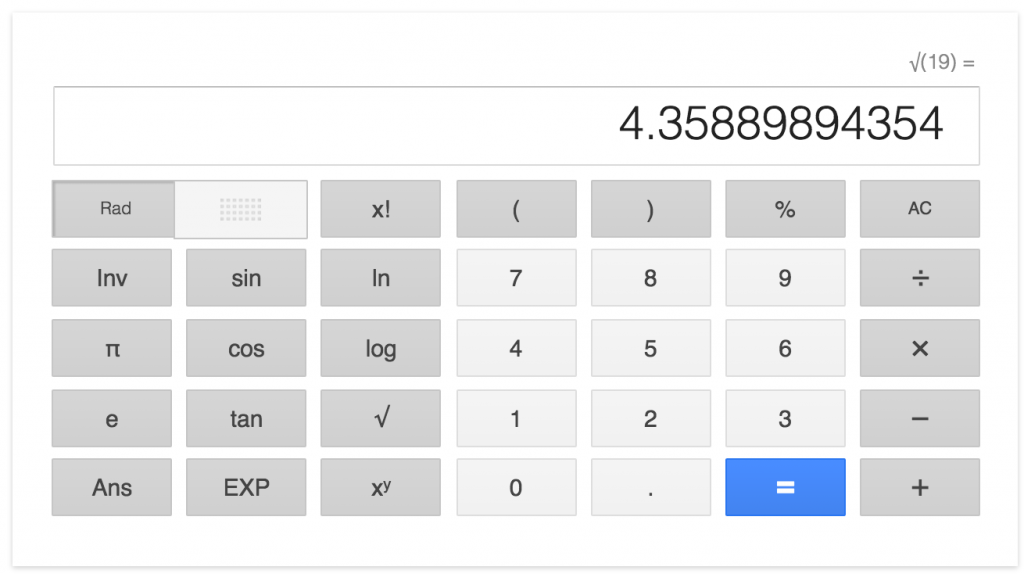
うん！

たしかにあってる！

√19の小数第2位は「5」だもんね。

計算機で確認できるから便利だ^^

まとめ：平方根の近似値の求め方は粘り強さでかとう！

平方根の近似値の求め方はシンプル。

1の位からじょじょに範囲をせばめればいいんだ。

池の魚をおいつめるみたいだね。

計算は大変だけど、気合と根性でせばめていこう！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。