確率の問題の解き方がわからない!!
こんにちは!この記事をかいているKenだよ。チャーハンは万能だね。
確率の問題ってむずいよね??
場合の数をかぞえたり、
樹形図をかいてみたり・・・・
なんだろう、
大忙しだ。
っていうか、解き方がよくわからないときが多いはず。
そこで今日は、
中学数学でつかえる確率問題の解き方を5ステップで解説していくよ。
テスト前に参考にしてみてね。
確率の問題の解き方がわかる5ステップ
確率の問題は5ステップでとけるよ。
- 樹形図をかく
- すべての場合の数を調べる
- あることがらの場合の数を調べる
- 確率を公式で計算
- 約分する
つぎの例題で解き方を解説していくね^_^
例題
A・B・Cの3枚のカードを並べるとき、BとCが隣り合わせになる確率を求めよ。

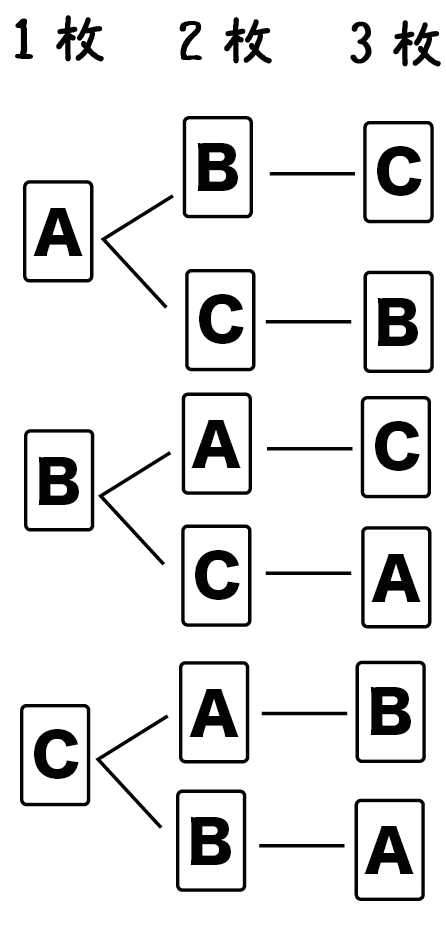
Step1. 樹形図をかく!
まず樹形図をかいてみよう。
中学数学では場合の数を調べる方法は、
樹形図しか、ない。
だから、
めんどいかもだけど樹形図をかいてみよう。
カードA・B・Cの並べ方はつぎのようになるよ。
Step2. 「すべての場合の数」を数える!
樹形図から「すべての場合の数」を調べよう。
いちばん右の「実の数」を数えればいいんだ。
例題の樹形図では「6」だね??
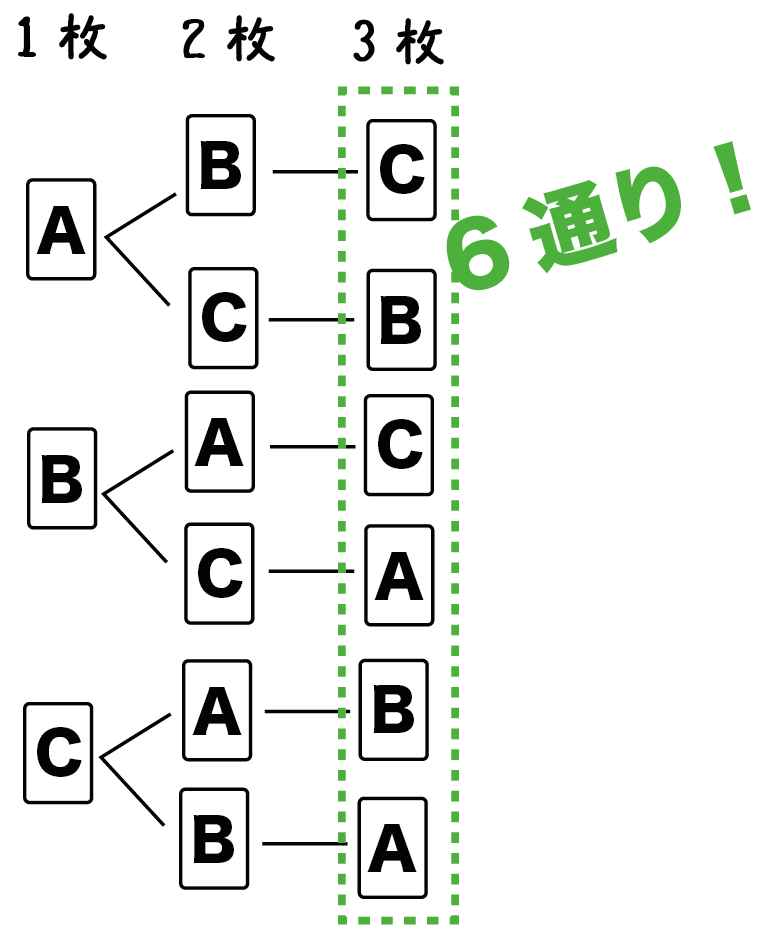
つまり、
すべての場合の数は「6通り」あるってことさ。
Step3. 「あることがら」の場合の数をしらべる!
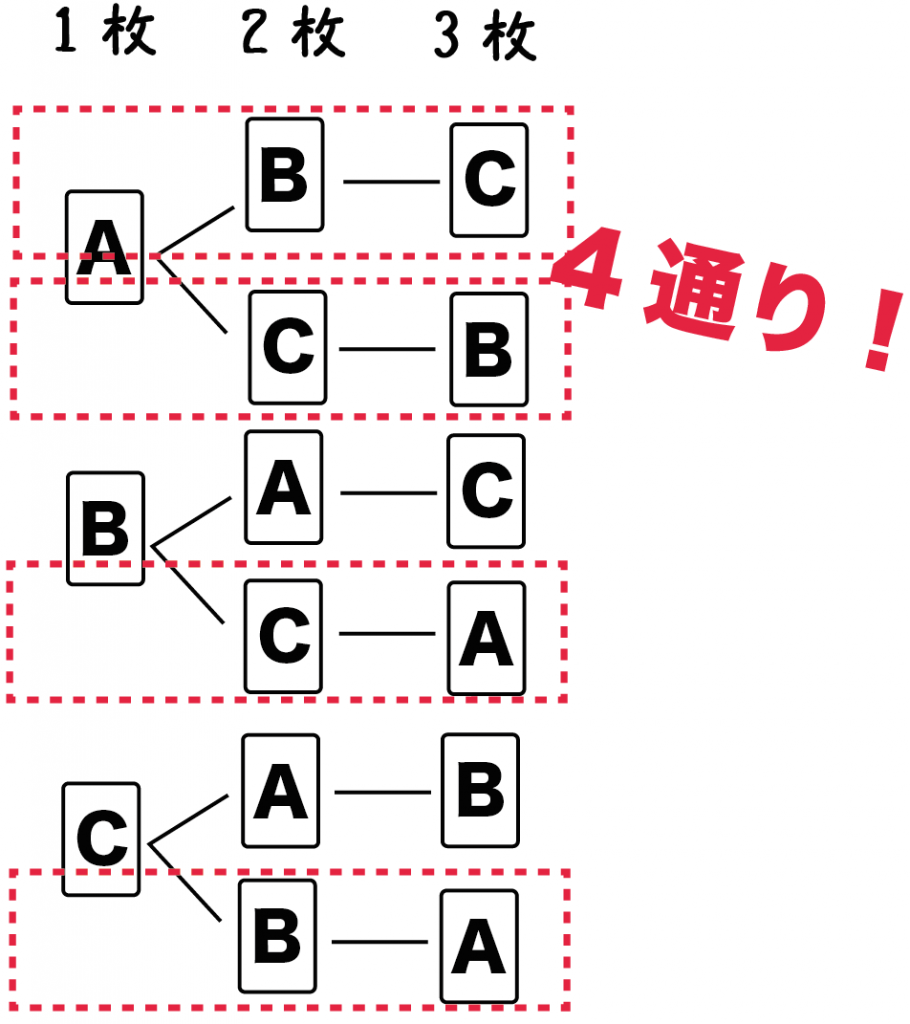
「求めたいことがら」の場合の数をしらべよう。
例題でいうと、
BとCが隣り合わせになる場合の数
をしらべればいいんだ。
樹形図をみてみると、
4通りってことがわかるね。
Step4. 公式で確率を計算!
あとは確率の公式で計算するだけ。
あることがらAが起きる確率は、
(Aが起きる場合の確率) = (ことがらAが起きる場合の数)÷(すべての場合の数)
だったよね??
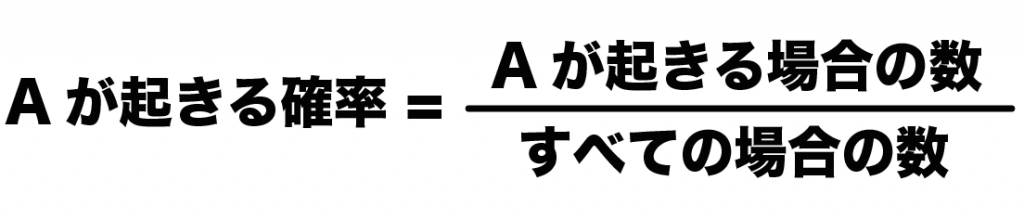
これを使おう。
例題でいうと、
- BとCが隣り合わせになる場合の数:4
- カードの並べ方すべての場合の数:6
だ。
ってことは確率の計算式をつかえば、
(BとCが隣り合わせになる確率)
=(BとCが隣り合わせになる数)/(すべての場合の数)
= 4/6
になるはず。

Step5. 約分する!
最後に約分しよう。
約分しなくても間違えじゃない。
だけど、先生によっては×にされるかもしれない。
約分して分数を簡単にしよう。
例題の確率は、
6分の4
だったよね??
こいつを約分すると、
3分の2になる。

これがきれいな確率の答えだよ^^
まとめ:「約分」までが確率の問題の解き方!
帰るまでが遠足
ってよくいうよね。
だけど、確率では、
約分までが確率だよ。
もう一度約分できるか疑ってみよう!
そんじゃねー
Ken

Qikeruで執筆しています。
「教科書、もうちょっとおもしろくならないかな?」
そんな想いで始めました。


証明問題の応用になるとどうしたらいいですか?
応用でも基本は一緒かな!
問題をたくさん解いてパターンに慣れよう
もうすぐ中間テストがあるのですが、私も確率の問題が解けません!
特に樹形図の書き方が、よくわかりません。授業でもあまり意味がわかりません。細かく教えて下さい!
お願いします!!
>もうすぐ中間テストがあるのですが、私も確率の問題が解けません!
特に樹形図の書き方が、よくわかりません。授業でもあまり意味がわかりません。細かく教えて下さい!
お願いします!!
樹形図のかきかたは練習しまくって覚えよう。
確率の問題はある程度パターンが決まってるから、問題をたくさん解くの大事
2個のサイコロを同時に投げる時、同じ目が出る確率
>2個のサイコロを同時に投げる時、同じ目が出る確率
サイコロが2個の問題は表をかけばいいね。
詳しくは「サイコロ2個の確率問題」を読んでみて
あるテキストの問題です、
「ある花壇に、3つの区切りがあり、赤、白、黄色の花の種が1つずつあります。
しかし、種を全て落としてしまい、見分けがつかなくなってしまいました。
そこで、右、真ん中、左の3つの区切りに1つずつ植えることにしました。
この時、真ん中に黄色の花が咲く確率を求めなさい。」
↑はどうやって解けばいいでしょうか、授業などでも全く取り扱ってなかったタイプの問題です
>ある花壇に、3つの区切りがあり、赤、白、黄色の花の種が1つずつあります。
しかし、種を全て落としてしまい、見分けがつかなくなってしまいました。
そこで、右、真ん中、左の3つの区切りに1つずつ植えることにしました。
この時、真ん中に黄色の花が咲く確率を求めなさい。
真ん中に黄色が来るパターンは、
赤黄白
白黄赤
の2パターンだね。赤黄白を並び替えるすべての場合の数を計算してそいつでこの場合の数を割れば良さそう
5本のうち,あたりが2本はいっているくじがあり、このくじを、A,Bの2人がこの順に1本ずつ引くときの樹形図の作り方をご教示ください。
>5本のうち,あたりが2本はいっているくじがあり、このくじを、A,Bの2人がこの順に1本ずつ引くときの樹形図の作り方をご教示ください。
あたりを◯、ハズレを×として樹形図を書いてみよう。
Aを1つ目、Bを2つ目にかいて行こうぜ。
右の図のように正方形ABCDの頂点Aの上に点Pがある。一個のサイコロを投げ、出た目と同じ数だけ頂点を矢印の向きに点Pが移動する。サイコロを2回投げた時点Pが頂点Bの上にある確率を求めよ。
箱の中に -1,2,-3,4,-5 の数が一つずつ書かれた五枚のカードが入っている。
この箱の中から同時に3枚のカードを取り出すとき、取り出したカードに書かれた数の積が負の数となる確率を求めなさい。
解説には3枚のカードの全部の取り出し方は、取り出さない2枚のカードの選び方と等しく、10通りある。
と書かれているのですが、理解できなかったので、詳しく教えて欲しいです。よろしくお願いします。
>右の図のように正方形ABCDの頂点Aの上に点Pがある。一個のサイコロを投げ、出た目と同じ数だけ頂点を矢印の向きに点Pが移動する。サイコロを2回投げた時点Pが頂点Bの上にある確率を求めよ。
2回投げてBに来るってことは、
でための合計が5、もしくは9の場合ってことね。
こいつらの場合の数を数えて確率を求めてみよう。サイコロ2つのパターンは表を書くと数えやすいよ
>箱の中に -1,2,-3,4,-5 の数が一つずつ書かれた五枚のカードが入っている。
この箱の中から同時に3枚のカードを取り出すとき、取り出したカードに書かれた数の積が負の数となる確率を求めなさい。
正の数になる場合の数の方が圧倒的に少なさそうだから、正の数になる確率を求めて1から引いてみるのが早さそう。
正の数になるのは2と4が組み合わさった時と、-1,-3,4で合計が0になる時だけだね
習ったことが無い問題です、解き方がわかりません
Q.1個のさいころを4回投げるとき、6の目が1回でも出る場合とでない場合とでは、どちらの方が起こりやすいかを考え、その理由を説明しなさい。
>Q.1個のさいころを4回投げるとき、6の目が1回でも出る場合とでない場合とでは、どちらの方が起こりやすいかを考え、その理由を説明しなさい。
でない場合の方が確率は計算しやすいね。
でない方の確率がわかったら、1からその確率をひくと「1回でもでる確率」が算出できるはず
素数の語呂合せてありますか?
>素数の語呂合せてありますか?
素数の覚え方を読んでみて
樹形図をかくときのコツってありますか!?
>樹形図をかくときのコツってありますか!?
抜け漏れなく書こう!練習あるのみ
100円玉50円玉10円玉のいずれかを使って370円にする方法は何通り?
枚数の制限ないなら結構ありそうだな!
座標平面上で原点にある点pを1枚の硬貨を1回投げるごとに表が出るとx軸の正の方向に1だけ移動し裏が出るとy軸の正の方向に1だけ移動する。という問題があります。この硬貨を2回投げる時の点pの座標が(1・1)になる確率が分からないので教えてください。
確率の応用の問題で頂点に1から6までの番号をつけた1辺の長さが1cmの正6角形がある。いま大小2つのサイコロを同時に1回投げ出た目の数と同じ番号の頂点をそれぞれ選ぶ。異なる2点を選んだ場合はその2点を結ぶ線分を引く。という問題があります。その長さ1cmの線分が引ける場合は何通りあるかの問題と長さ2cmの線分が引ける確率の問題が分かりません。教えてください。よろしくお願いします。
確率の階段の問題がわかりません。教えてください。お願いします。
トランプのジョーカーとキング、クイーンの組み合わせになる確率はどうやって求めたらいいんですか?教えて下さい!!後、ステップ演習という参考書のステップBの問題が全然分からないんですけど、やり方のコツがあったら教えてくだい!お願いします!
どうすればサイコロの確率を求められるのか
くじが10本あり、このうち4本が「当たりくじ」である。このくじから3本を引くとき、2本だけ当たる確率は?
の解き方を教えて下さい。