【平面図形】5ステップでできる！点対称移動の作図・書き方

点対称移動の書き方がいまいちわからない？？

こんにちは、この記事をかいているKenだよ。コーヒー豆が好きだね。

前回まで、

• 平行移動
• 回転移動
• 対称移動

っていう3つの図形移動を勉強してきたね。もう正直、図形なんて移動させたくないでしょ？？笑

だけど、今日はもう1つだけ知っておくべきことがあるんだ。

それは、

点対称移動の書き方・作図

というやつさ。

点対称移動は「回転移動の1種」だった？？

点対称移動ってきくと、

また図形移動が増えんのかよ？！？　ざけんな！

っていいたくなるよね笑

だけど、点対称移動は回転移動の一種なんだ。

回転移動にもいろんなやつがいて、そのうちの1人だと考えてもらって構わない。

たとえば、「回転移動の図形をあつめたクラス」があったとしたら、点対称移動はこころせましと座っているうちの一人。

クラスにもいろんな奴がいると思うけど、回転移動のクラスだって同じさ。

それじゃあ、どんな奴が点対称移動になるのかって気になるよね？？

じつは、

回転移動のうち、

回転角度が180°のものを「点対称移動」って呼んでいるんだ。

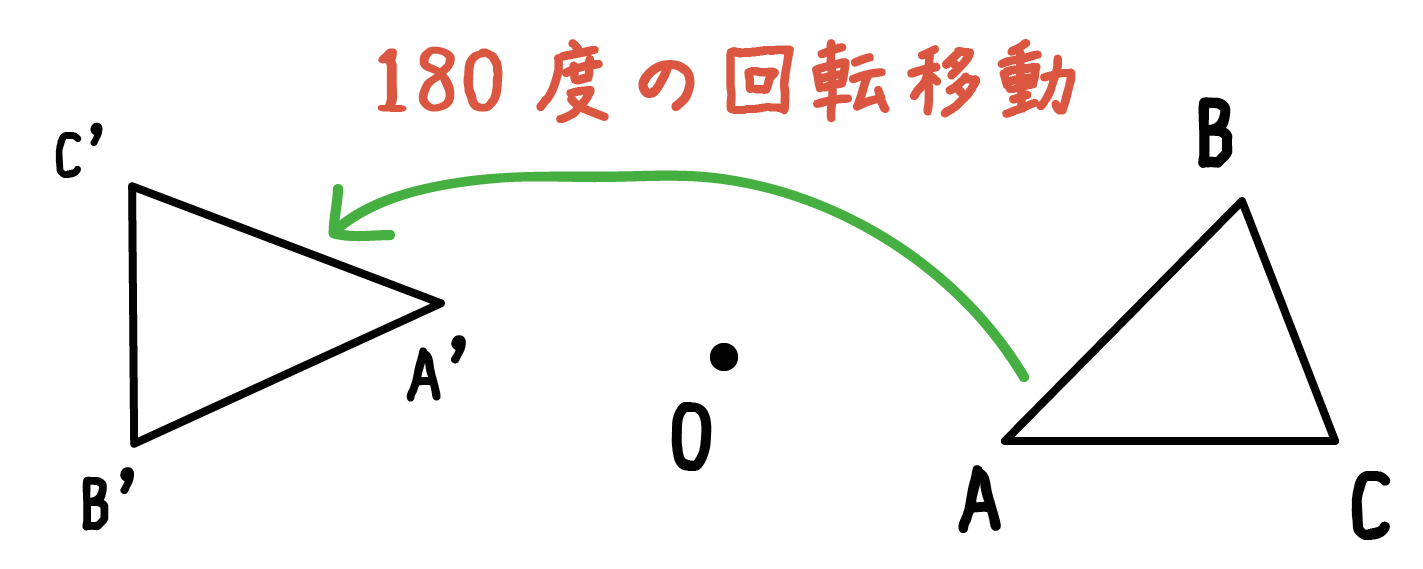
ちょっと点対称の正体がわかったでしょ？？

つぎは点対称移動の書き方をみていこう！

点対称の図形の書き方ってなにを使えばいいの？？

点対称移動の作図をマスターするためには、

点対称移動の図形の性質

をおさえておくべきなんだ。平行移動でも回転移動でもそうだったように、性質を知っていると移動方法がわかってくるんだ。

教科書では、

点対称移動では、対応する点と回転の中心はそれぞれ1つの直線上にあります。

って書いてあるね。つまり、

「対応する点」をむんでできた直線の上に「回転の中心」があるってことになる。

たとえば、三角形ABCを回転の中心Oで点対称移動させたとしよう。

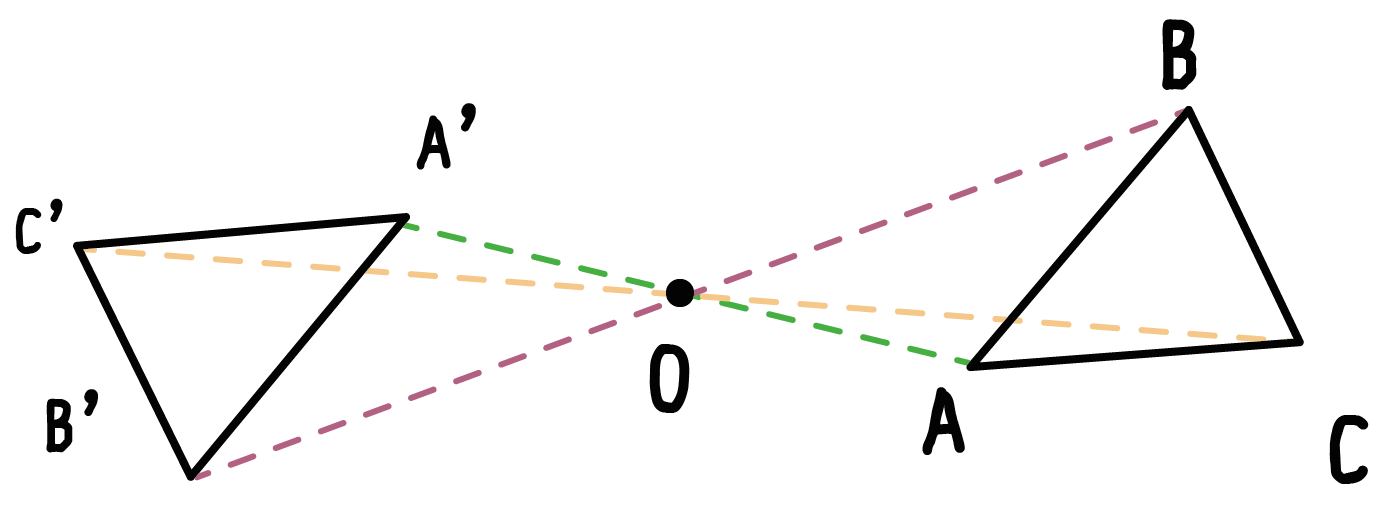
点対称移動後の三角形A’B’C’とすれば、

線分AA’、BB’、CC’には必ず「回転の中心O」がふくまれているんだ。

この性質を使ってガンガン点対称移動させまくろう！！

5ステップで完成！？　点対称移動の書き方・作図方法

それじゃあ、点対称移動の書き方をみていこう。

三角形ABCを「回転の中心O」で点対称移動させよ！

っていう例題をつかって解説していくね^^

Step 1. 　「ある頂点」と「回転の中心」を直線でむすぶ

最初に、「1つの頂点」と「回転の中心」を直線でむすんであげよう。

たとえば、三角形ABCの「頂点A」と「回転の中心O」って感じで↓↓

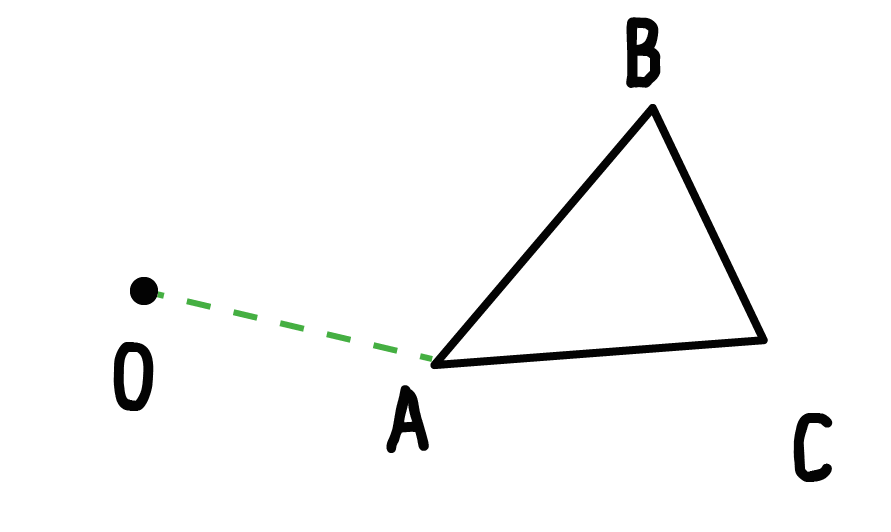
定規をつかってむすんであげてね^^

Step 2. 頂点と「回転の中心」の距離を測る

つづいては、さっきできた新しい線分の長さを測ってあげよう。

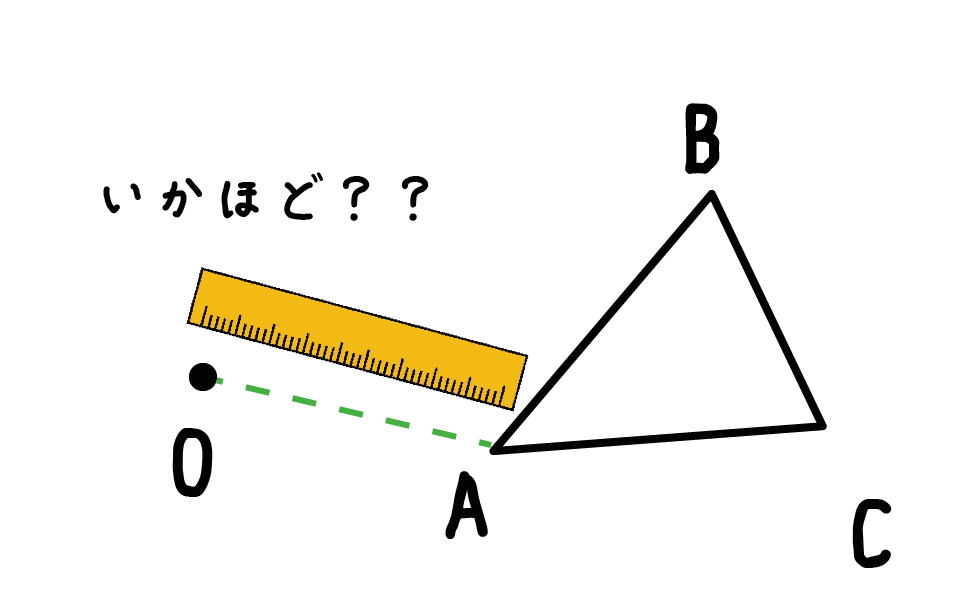
つまり、「図形の頂点」と「回転中心の距離」をはかるってことだね。

こいつを定規でびしっと測ってやろう。

Step 3. 線分をのばす

つぎは、さっき作った新しい線分を伸ばしてあげよう。

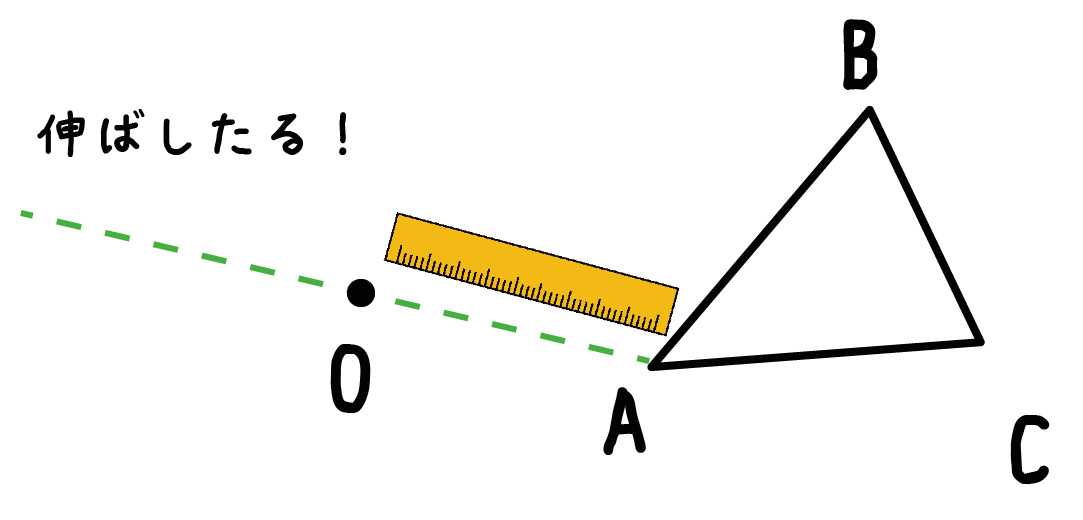
線分を伸ばす方向は移動させる図形とは逆側だ。

ぐんぐん適当にのばしておこう！

Step 4. 　ステップ2で測った長さのところで直線上に点をうつ

つぎは、伸ばした直線の長さを決めてやるフェーズだ。

ステップ2ではかった長さだけ、回転の中心Oから離れたところで点をうつんだ。

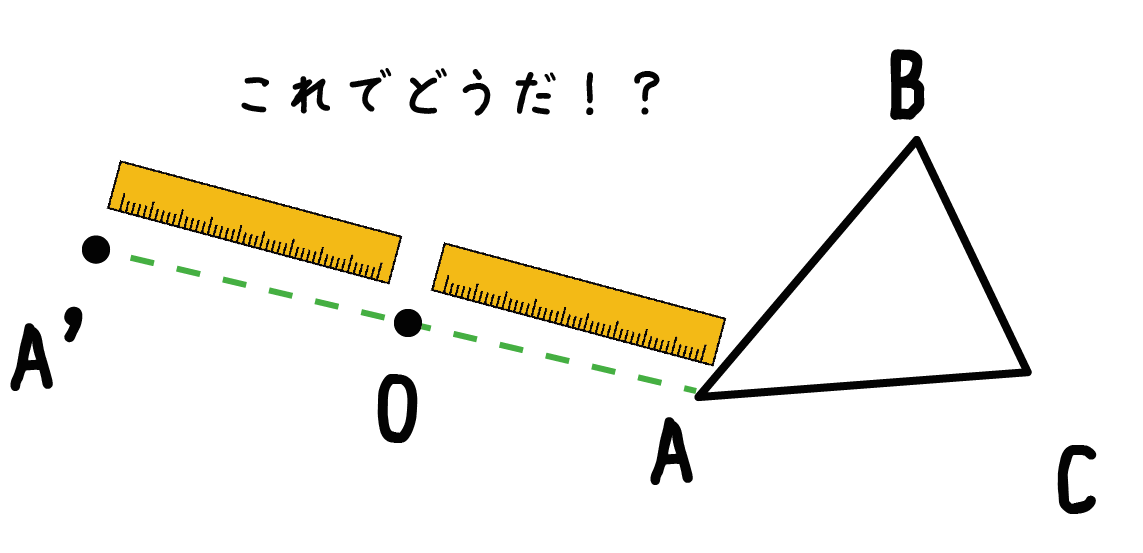
例題でいうと、点A’がそれにあたる。

これが三角形ABCの頂点Aに対応するA’になるね。

Step 5. ステップ1~4を他の頂点でもくり返す！

ここまでのステップを他の頂点でもやってみよう！！

例題でいうと、残りの頂点BとCだね。

こいつらもAと同じように、結んだり点を打ったりすると、

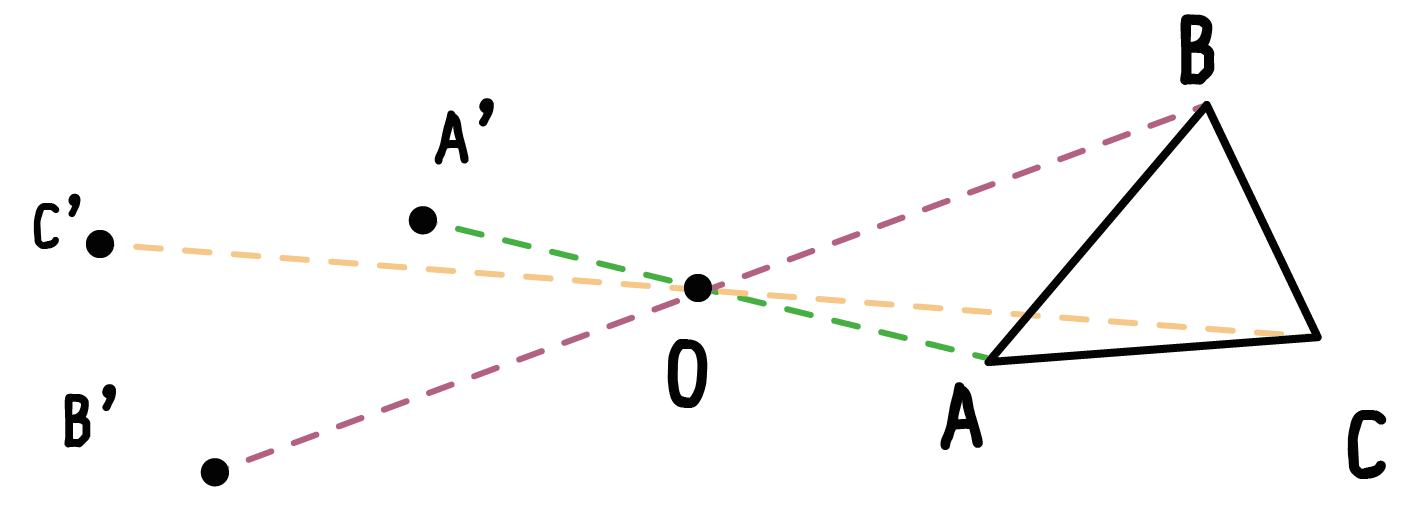
こうなるね。そんで新しくできた移動後の頂点たち（A’、B’、C’）をむすんであげると、

点対称移動したあとの三角形A’B’C’があらわれるでしょ？？

これで点対称移動はおしまい！

ふう、疲れたー

まとめ：点対称移動は回転移動の一種である

点対称移動は回転移動のうちの1種。

だから、とくに新しいことを覚える必要なんてない。

ただ、回転移動と同じ方法で作図するのはちょっと疲れるんだ。

めんどくさがり屋な奴こそ、点対称移動の書き方をおぼえておこう笑

つぎは点対称と線対称の違いについて書いてみるねー！

そんじゃねー

Ken

Ken

Qikeruで執筆しています。

「教科書、もうちょっとおもしろくならないかな？」

そんな想いで始めました。